Устойчивое равновесие кубика в воде.

[Viktor92]

Если в моей вычисленной работе, устремить $S$ к бесконечности и положить $\rho=\rho_{\text{ж}}$, то получается нулевая работа сил тяжести, хотя она там вполне себе работает, видно то что я нашёл не совсем работа сил тяжести, а вот что... надо подумать...

[Sender]

Viktor92 в сообщении #1070174 писал(а):

Если в моей вычисленной работе, устремить $S$ к бесконечности и положить $\rho=\rho_{\text{ж}}$, то получается нулевая работа сил тяжести

Собственно, не вижу ничего удивительного - сначала вы вытесняете некоторый объём жидкости на поверхность, а потом с поверхности заполняете этот объём той же самой жидкостью .

[Munin]

Skeptic в сообщении #1070085 писал(а):

Эксперимент сам учитывает плотность материала. Это не зависит от желания экспериментатора. Рассуждающие вне опыта обязаны учитывать плотность материала.

А вот экспериментаторы обязаны плотность указывать. Иначе их отчёты об эксперименте становятся бесполезными.

[amon]

Sender в сообщении #1070097 писал(а):

Хорошо, не могли бы вы привести ваши выражения для потенциальной энергии в случае бруска, плавающего плашмя и вертикально,

Виноват, некогда написать было, поэтому попытался перевалить все на Вас - не получилось ;)

Итак, у нас есть цилиндрический тазик (океан), в который мы втыкаем цилиндрическую же палку и пытаемся найти изменение потенциальной энергии. Что бы не запутаться, будем считать разность потенциальной энергии таза с палкой и без палки. Если мы все сделаем правильно, то от таза в ответе ничего остаться не должно.

Вложение:

bob.GIF [ 3.17 Кб | Просмотров: 1860 ]

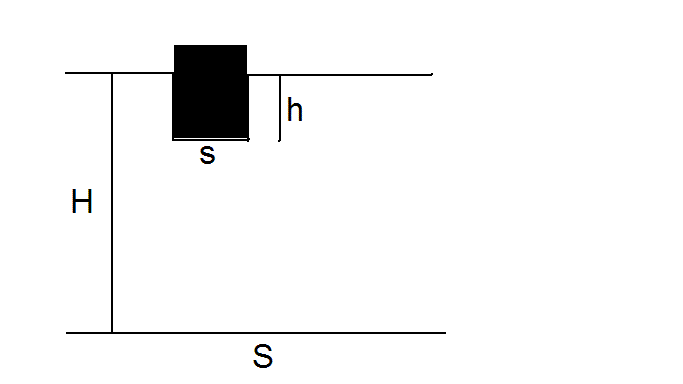
Я не Айвазовский, поэтому нарисовал как мог. Объем таза (океана) $V=HS$, объем погруженной части тела - $v=hs$. Потенциальная энергия океана $U_0=\frac{1}{2}g\rho_\text{ж}SH$. При подсчете изменения энергии надо узнать на сколько сдвинется центр масс системы океан+палка от того, что мы засунем палку в океан. Это изменение состоит из двух частей: изменения положения цм океана из-за того, что в нем просверлили дырку размером с погруженную часть, и изменение цм из-за положенной в дырку палки.
Вторая часть тривиальна, и точно положительна, поэтому займемся первой.

Мы во-первых, вылили в океан жидкость объемом $v$, а во-вторых, сделали у поверхности дырку размером $h\times s$. В результате первого действия уровень океана поднялся на величину $\Delta H=\frac{v}{S}$, что увеличило потенциальную энергию системы на $\Delta U_1=\frac{1}{2}g\rho_\text{ж}Hv$. Высверливание дырки уменьшает потенциальную энергию на $\Delta U_2=-g\rho_\text{ж}v(H+\Delta H-\frac{h}{2})$. Складываем и получаем

$$ \Delta U=\frac{g\rho_\text{ж}vh}{2}-\frac{g\rho_\text{ж}v^2}{S}. $$

Второй член для океана - ноль, а первый равен Вашему, но отличается знаком. Ошибка, IMHO, в том, что нельзя считать уровень океана неизменным. Да, сдвиг мал, но и масса огромна.

[Munin]

amon в сообщении #1070199 писал(а):

Если мы все сделаем правильно, то от таза в ответе ничего остаться не должно.

Нет, почему? Только в пределе $S\to\infty.$

[amon]

Munin в сообщении #1070203 писал(а):

Нет, почему?

Член, зависящий от формы, я сначала потерял, а потом первые фразы лениво исправлять было.

[Sender]

amon в сообщении #1070199 писал(а):

Вторая часть тривиальна, и точно положительна

Не вполне понятный момент, где у вас палка находилась до помещения в океан, что при погружении в него её потенциальная энергия увеличилась?

amon в сообщении #1070199 писал(а):

Второй член для океана - ноль, а первый равен Вашему, но отличается знаком.

Хм, попробуем сравнить первый член вашего выражения: $\frac{g\rho_\text{ж}vh}{2}$
с моей версией:

Sender в сообщении #1069660 писал(а):

В случае, когда брусок плавает вертикально, она равна $U_2=\frac{1}{2}\rho_\text{ж}ga^2(\frac{\rho}{\rho_\text{ж}}b)^2=\frac{\rho^2g}{2\rho_\text{ж}}a^2b^2$

, учтя, что в данном случае $h=b\frac{\rho}{\rho_\text{ж}}$, $v=a^2b$.
Не понимаю, где здесь отличие в знаке.

[amon]

Sender в сообщении #1070229 писал(а):

Не понимаю, где здесь отличие в знаке.

Здесь:

$$U= g\int\limits_{V_0}\rho z\mathrm{dV}- g\int\limits_{V_\text{погр}}\rho_\text{ж} z\mathrm{dV}.$$

У меня оба члена имеют одинаковые знаки. Энергия океана возрастает как от того, что на его поверхность положили палку, так и от того, что в воде образовалась ямка. Последнее не удивительно, поскольку в противном случае поверхность бы сама "дырявилась", раз это энергетически выгодно.

[Sender]

amon в сообщении #1070242 писал(а):

У меня оба члена имеют одинаковые знаки.

Я брал за начало отсчёта уровень воды и направлял ось вверх, так что $z$ под интегралом во втором слагаемом отрицателен, что с учётом знака даёт положительность второго члена. А вот у вас-таки получается самодырявящийся океан.

-- Ср ноя 04, 2015 20:03:01 --

(Оффтоп)

Вообще, у меня стойкое ощущение, что в этой теме мы занимаемся преимущественно толчением воды в ступе :-)

[amon]

Sender в сообщении #1070249 писал(а):

что с учётом знака даёт положительность второго члена.

Давайте все-таки как-нибудь договоримся. Если второй член положителен, то откуда минус здесь:

Sender в сообщении #1069920 писал(а):

Если угодно, полная потенциальная энергия системы в первом случае
$U_1'=U_1+\rho g a^2b(\frac{a}{2}-a\frac{\rho}{\rho_\text{ж}})=\frac{\rho g}{2}a^3b(1-\frac{\rho}{\rho_\text{ж}}),$

и как тогда понимать это?

Sender в сообщении #1070055 писал(а):

Боюсь, что да. Допустим, плотность тела равна плотности жидкости. Моя формула даст нуль потенциальной энергии.

[Sender]

amon в сообщении #1070253 писал(а):

Давайте все-таки как-нибудь договоримся. Если второй член положителен, то откуда минус здесь:Sender в сообщении #1069920

писал(а):
Если угодно, полная потенциальная энергия системы в первом случае
$U_1'=U_1+\rho g a^2b(\frac{a}{2}-a\frac{\rho}{\rho_\text{ж}})=\frac{\rho g}{2}a^3b(1-\frac{\rho}{\rho_\text{ж}}),$

Здесь пресловутый второй член - это $U_1$, равный $\frac{\rho^2 g}{2\rho_\text{ж}}a^3b.$
А вот $\rho g a^2b(\frac{a}{2}-a\frac{\rho}{\rho_\text{ж}})$ - это потенциальная энергия бруска. При плотности тела, равной плотности жидкости, она отрицательна, т.к. за начало отсчёта потенциальной энергии бруска я брал положение, где центр его масс лежит на поверхности жидкости.

[Viktor92]

Sender в сообщении #1070177 писал(а):

Собственно, не вижу ничего удивительного - сначала вы вытесняете некоторый объём жидкости на поверхность, а потом с поверхности заполняете этот объём той же самой жидкостью

Так то оно так, но проводя все выкладки я предполагал, что мы опускаем палку вертикально из положения когда её нижний конец касается поверхности воды, точнее не мы, а сила тяжести, причем квазистатично. Допусти эта палка у нас имеет такую же плотность, как и вода, а ещё лучше пусть она сама состоит из воды, и если у меня работа силы тяжести получилась равной нулю, то ничего не мешает появлению на поверхности океана спонтанных столбов жидкости Но тут уже наверно вступает в игру направление протекания процессов - беспорядок должен возрастать.

[amon]

Sender в сообщении #1070256 писал(а):

Здесь пресловутый второй член - это $U_1$, равный $\frac{\rho g}{2}a^3b$

Угу. Наконец понял. Но осадок все равно остается. Завтра попытаюсь сформулировать.

[Sender]

Viktor92 в сообщении #1070155 писал(а):

$dU_{\text{б}}=-(\frac {b}{2}-h)a^2b \rho g=(-\frac {b}{2}+\frac {a^2 \rho b}{\rho_{\text {ж}}(S-a^2)})a^2b \rho g $

Вот это место проверьте ещё раз, мне кажется, тут ошибка.

[Skeptic]

Отклоним плавающий кубик от положения равновесия. Рассмотрим вертикальное сечение кубика, проведённое через его центр тяжести, точку $O$. Четырёхугольник $ABCD$ образует подводный объём кубика. Из точки $O$ проведём вертикаль $OE$, совпадающую с вектором веса кубика. Отрезок $OE$ разделит подводный объём кубика на два четырёхугольника $AOED$ и $BOEC$. Эти четырёхугольники между собой равны. Подъёмные силы этих четырёхугольников также равны, но вращают кубик в противоположные стороны. Направление вращения кубика будет определять сила, центр высоты (ЦВ) которой расположен дальше от вертикали силы тяжести $OE$. Наложим четырёхугольник $AOED$ на четырехугольник $BOEC$, повернув его вокруг отрезка $OE$. Расположение ЦВ не совпадающих частей этих четырёхугольников: треугольников $EHF$ и $BHC$, определяют направление вращения всего кубика. Очевидно, что ЦВ треугольника BHC расположен дальше от отрезка $OE$, чем ЦВ треугольника $EHF$.
Таким образом, выведенный из равновесия плавающий кубик будет стремится повернуться против часовой стрелке, и займёт равновесное положение вверх вершиной.