Экзотическое состояние атома водорода уравнение Дирака

[amon]

Helium в сообщении #1006548 писал(а):

$l=-\tfrac{1}{2}$ и $m=0$

Опаньки! Слона-то я...

[Helium]

надо подумать

[Helium]

Нет опять только на полюсах по очереди есть сингулярность. Но квадратично интегрируема так как
множитель $\sin \left(\theta \right)$ все исправляет. Вопрос о применяемости комбинации по очереди остается.
Второй вариант использовать так как есть с сингулярностью в одном полюсе так как интеграл сходится.

[Helium]

Munin в сообщении #1006496 писал(а):

Например, там написано про поле спина, а вы-то ищете не поле спина.

То что написано это универсальный подход при решении углового уравнения. Независимо это поле спина или орбитального движения.Этот подход верный или нет я не знаю.
Я ищу не поле спина? Наоборот я ищу именно поле спина. Более того я считаю, что для атома водорода существует только поле спина и нету орбитального движения.
Но по моему подходу, спин может принимать всю гамму значений как целые так и полуцелые начиная от $-\frac{1}{2}$. А не только $\pm \frac{1}{2}$ как принято считать.

[Munin]

Helium в сообщении #1006747 писал(а):

То что написано это универсальный подход при решении углового уравнения.

Нет. Это частный подход при определённых условиях. А вот эти условия вы пропустили мимо ушей. (Или чем вы там читаете, точнее, не читаете.)

И вы так и не написали источник цитаты. Пора звать модераторов?

Helium в сообщении #1006747 писал(а):

Независимо это поле спина или орбитального движения.

Нет. Зависимо. Это каждый троечник знает - что для спина полуцелые $l$ и $m$ разрешены, а для орбитального момента - запрещены. А каждый отличник знает, почему. В учебнике всё написано.

А вот вы не тянете даже на троечника.

Helium в сообщении #1006747 писал(а):

Я ищу не поле спина? :-) Наоборот я ищу именно поле спина.

Нет. Вы решаете уравнение Шрёдингера без спина.

По сути, вы даже не написали, что решаете, так что приходится догадываться по вашему невнятному бормотанию.

Helium в сообщении #1006747 писал(а):

Более того я считаю, что для атома водорода существует только поле спина и нету орбитального движения.

Этот ваш бред никак не связан с той задачей, которая обсуждается в этой теме.

А в реальности вся математическая теория - единое целое. В ней всякая деталь на своём месте, подогнана, состыкована с другими, и работает вместе с ними.

Helium в сообщении #1006747 писал(а):

Но по моему подходу

Нету у вас никакого подхода, а есть бред. А вот почему это бред - мы вам объясняли-объясняли...

Дед бил-бил, баба била-била...

- безрезультатно.

[Prikol]

amon в сообщении #1006178 писал(а):

Уважаемый Prikol,
Вообще-то я не знаю, почему я обязан отвечать на Ваше выступление. Я не имею ни малейшего желания дискутировать или мериться толщиной индекса Хирша с Вами.

Вы о каком выступлении? Был просто уточняющий вопрос по поводу вашего поста.

amon в сообщении #1004625 писал(а):

Направление спина - это обычное 3-х мерное направление.

То есть, вы сказали, что спин имеет направление. Я засомневался и предложил вам указать это направление для простейшей ситуации, когда волновая функция задана. Вся информация о состоянии системы содержится в ее волновой функции. Это должно быть проще, чем провести измерение и по его результатам попытаться восстановить какие-то параметры системы.

Prikol в сообщении #1006089 писал(а):

Волновая функция этого состояния известна. Вопрос. Куда направлен вектор углового момента?

Теперь вы говорите другое о направлении спина:

amon в сообщении #1006178 писал(а):

Вопрос о том, куда в квантовой механике направлен вектор [...] столь же глубокомыслен, как вопрос о положении квантовой системы на фазовой плоскости.

Получается из вашей первой цитаты, что спин имеет направление, но из второй цитаты следует, что об этом направлении вроде бы нельзя спрашивать.

Еще более радикальную позицию имеет g______d

g______d в сообщении #1006095 писал(а):

Prikol в сообщении #1006089 писал(а):

Волновая функция этого состояния известна. Вопрос. Куда направлен вектор углового момента?

Направление? Какое направление? Орбитальный момент -- это оператор [...]

То есть, это не вектор, а оператор.

-- 22.04.2015, 22:00 --

Cos(x-pi/2) в сообщении #1006205 писал(а):

Prikol в сообщении #1006140 писал(а):

Берем атом какого-нибудь вещества и говорим - у него (после выделения этого состояния) $l=3$ и $m=2$. В том, что $m=2$ можно убедиться в эксперименте Штерна-Герлаха. А в каком эксперименте можно увидеть направление $l$?

Дык опять же в эксперименте Штерна-Герлаха. Надо только понимать, что "увидеть" направление $\langle \, \mathbf{l} \, \rangle$ удастся не "за раз", а лишь в результате анализа накопленной статистики разных измерений. Это выглядит примерно так.
...
Вместе с результатами первой серии измерений (где флуктуаций не было, так что $\langle l_z\rangle=m=2$) в итоге имеем экспериментальную информацию об усреднённом векторе момента. В данном примере согласно теории должно получиться $\langle l_x \rangle = \langle l_y \rangle = 0.$

Вы описали эксперимент для определения среднего в серии измерений направления. Оно (вроде бы) совпало с осью $z$.

Что если мы всетаки вернемся к вопросу об определении всего, что надо, по заданной волновой функции. Пусть это атом водорода с некоторыми заданными $n, l, m$ (но не суперпозиция разных состояний, спин пока игнорируем).

Посмотрев на часть волновой функции зависящей от угла $\varphi$ мы сразу, без всяких измерений можем сказать, какое значение $m$ получится в первом же эксперименте. Мы можем также указать направление оси, вдоль которой всегда будет получаться это значение $m$

Но где в этой заданной волновой функции "прячется" направление полного углового момента?

[Cos(x-pi/2)]

Munin в сообщении #1006832 писал(а):

Helium в сообщении #1006747 писал(а):

То что написано это универсальный подход при решении углового уравнения.

Нет. Это частный подход при определённых условиях. А вот эти условия вы пропустили мимо ушей. (Или чем вы там читаете, точнее, не читаете.)

И вы так и не написали источник цитаты. Пора звать модераторов?

ТС цитирует альта, отвергающего КТП и продвигающего выдуманную им "концепцию полей движения" (pdf c вариантом такого источника нагугливается на запрос "применение нового формализма к решению задач об одноэлектронном атоме"). Пока ТС не возьмётся реально изучать квантовую механику, говорить о ней всерьёз с ним бессмысленно...

[amon]

Уважаемый Prikol, как и предполагалось, дискуссия с Вами бесполезна. Все все поняли, общаться дальше по этой теме считаю бесполезным. За сим откланиваюсь.

[Prikol]

Cos(x-pi/2) в сообщении #1006907 писал(а):

ТС цитирует альта, отвергающего КТП и продвигающего выдуманную им "концепцию полей движения" (pdf c вариантом такого источника нагугливается на запрос "применение нового формализма к решению задач об одноэлектронном атоме").

Я еще на второй странице темы пытался "пробить" ТС на какую-либо связь с автором "концепции полей движения".

[Cos(x-pi/2)]

Prikol

Prikol в сообщении #1006896 писал(а):

Вы описали эксперимент для определения среднего в серии измерений направления. Оно (вроде бы) совпало с осью $z$.

Что если мы всетаки вернемся к вопросу об определении всего, что надо, по заданной волновой функции.

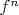
Согласно существующей квантовой теории, всё, что можно определить из волновой функции стационарного состояния, это именно средние значения физических величин (а также их степеней: если физ. величине $f$ в теории сопоставлен оператор $\hat f,$ то величине $f^n$ соответсвует оператор $\hat f^n.$) Ничего кроме средних по одной в.ф. стац. состояния определить нельзя.

Сюда же относятся и случаи, когда волновая функция стационарного состояния оказывается собственной функцией конкретного оператора $\hat f,$ - просто тогда среднее совпадает с собственным значением $f$ данного оператора на данной функции: $\langle f \rangle = f,$ так что $\langle f^n \rangle = f^n = {\langle f \rangle}^n,$ и это говорит нам об отсутствии квантовых флуктуаций величины $f$ в данном квантовом состоянии.

Prikol в сообщении #1006896 писал(а):

Посмотрев на часть волновой функции зависящей от угла $\varphi$ мы сразу, без всяких измерений можем сказать, какое значение $m$ получится в первом же эксперименте. Мы можем также указать направление оси, вдоль которой всегда будет получаться это значение $m$

Но где в этой заданной волновой функции "прячется" направление полного углового момента?

Да, потому что оператор проекции орбитального момента на ось $z$ имеет вид $\hat l_z=-i \frac{\partial}{\partial \varphi}$ и волновая функция $\psi_{nlm}(r, \theta, \varphi)$ как раз является собственной для этого оператора: она принадлежит собственному значению $l_z=m,$ ибо зависит от угла $\varphi$ как $e^{i m \varphi}.$ Получается, что $l_z$ не флуктуирующая величина в состоянии электрона с данной волновой функцией.

А остальная информация о полном угловом моменте "прячется" также в зависимости функции $\psi_{nlm}(r, \theta, \varphi)$ от угла $\theta.$ (А если Вы неплохо знаете квантовую механику, то вспомните ещё и такой факт: радиальная часть волновой функции ведёт себя при $r \to 0$ как $r^l,$ т.е. даже она содержит информацию о величине углового момента $l$ - потому что в радиальное уравнение входит центробежная энергия $\hbar^2l(l+1)/(2mr^2)$ (здесь $m$ - масса частицы)).

Операторы проекций орбитального момента $\hat l_x$ и $\hat l_y$ на оси $x$ и $y$ имеют более громоздкий вид. (Проще все эти операторы записать через декартовы переменные $x,y,z,$ но тогда и волновую функцию надо выразить через декартовы переменные; это всё упражнения для студентов, формулы есть в задачниках и учебниках, а мне вломно тут печатать длинные формулы. Правда, более-менее просто выглядит векторный оператор углового момента, разложенный по локальным ортам сферической системы координат:

$\mathbf{\hat l} = -i \mathbf{e}_{\varphi} \frac{\partial}{\partial \theta}+i\mathbf{e}_{\theta} \frac{1}{\sin \theta} \frac{\partial}{\partial \varphi}$ .

Скалярно умножив это выражение на орты декартовой с.к., найдёте отсюда операторы декартовых проекций углового момента, действующие на волновую функцию в сферической с.к.)

Средние значения проекций момента вычисляются с помощью этих операторов обычным для квантовой теории путём - как интеграл по всему объёму 3-мерного пространства (с координатами $r, \theta, \varphi$) от $\psi^* \hat f \psi.$ Вот и всё; собсно, это - азбучные истины, которые должны быть известны любому студенту, изучившему КМ.

Приличный студент должен знать также следующие факты. Из операторов проекций момента можно составить два вспомогательных оператора

$\hat l_{+}= \hat l_x+i \hat l_y$ ,

$\hat l_{-}= \hat l_x-i \hat l_y$ ,

обладающих примечательными свойствами: функция $\hat l_{+} \psi_{n,m,l}$ оказывается равной умноженной на некую константу функции $\psi_{n,l,m+1},$ а функция $\hat l_{-} \psi_{n,l,m}$ равна умноженной на константу функции $\psi_{n,l,m-1}.$ Обе получившиеся так функции ортогональны к исходной функции $\psi_{nlm}.$ Следовательно, среднее значение (вычисляемое как интеграл от $\psi_{nlm}^* \hat f \psi_{nlm}$ ) для этих операторов заведомо равно нулю, т.е.

$\langle \hat l_x+i \hat l_y\rangle =0$ ,

$\langle \hat l_x-i \hat l_y\rangle =0$ .

Отсюда, один раз складывая, а другой раз вычитая эти равенства, без долгих вычислений интегралов сразу получаем тот ответ, о котором говорилось выше:

$\langle l_x\rangle=0$ , $\langle l_y\rangle=0.$

[amon]

Cos(x-pi/2),
Не мучайтесь! Думаю, что уважаемый Prikol все это прекрасно знает. Проблема в том, что я "прикопался" к его неудачной фразе и он в качестве ответного шага пытается прикопаться к моей. При этом, стороны все уже давно поняли. Сейчас можно легко продолжить разбор полетов, поскольку фраза "Посмотрев на часть волновой функции зависящей от угла $\varphi$ мы сразу, без всяких измерений можем сказать, какое значение $m$ получится в первом же эксперименте" опять неудачная. Калибровочным преобразованием можно "часть волновой функции зависящей от угла $\varphi$ " закопать так глубоко, что глазом вообще ничего видно не будет. Тем не менее, все все понимают, и к словам не придираются.

[Helium]

Prikol в сообщении #1006930 писал(а):

Я еще на второй странице темы пытался "пробить" ТС на какую-либо связь с автором "концепции полей движения".

Действительно я не имею к этому никакого отношения. Но то что разные люди независимо друг от друга пришли к одной мысли, для меня это уже очень сильный сигнал, что тут кое что ценное имеется.

Munin в сообщении #1006832 писал(а):

Пора звать модераторов?

В дискуссионном разделе каждый имеет право на свое мнение. А что правильно и что нет покажет эксперимент.

Munin в сообщении #1006832 писал(а):

Нет. Вы решаете уравнение Шрёдингера без спина.

Да без спина потому что, в так называемом основном состоянии, спин равен нулю а не $\pm \frac{1}{2}$

Munin в сообщении #1006832 писал(а):

Этот ваш бред никак не связан с той задачей, которая обсуждается в этой теме.

Очень даже связан.
Сам электрон это плод решения уравнения Гельмгольца http://dxdy.ru/post886163.html#p886163 естественно со своей угловой частью.

[Cos(x-pi/2)]

Да, пожалуй, больше не стоит мучаться :)) Просто исходил из того, что если кто-нибудь ещё из молодёжи сюда заглядывает (форум-то публичный), то пусть увидит конкретную инфу, а не только троллинг и пустопорожнюю альтернативщину...

[Helium]

Munin в сообщении #1006832 писал(а):

А в реальности вся математическая теория - единое целое. В ней всякая деталь на своём месте, подогнана, состыкована с другими, и работает вместе с ними.

Вы забыли сказать существующая теория Да я согласен там сплошная подгонка.

[Prikol]

Cos(x-pi/2) в сообщении #1006952 писал(а):

Prikol в сообщении #1006896 писал(а):

Но где в этой заданной волновой функции "прячется" направление полного углового момента?

А остальная информация о полном угловом моменте "прячется" также в зависимости функции $\psi_{nlm}(r, \theta, \varphi)$ от угла $\theta.$ (А если Вы неплохо знаете квантовую механику, то вспомните ещё и такой факт: радиальная часть волновой функции ведёт себя при $r \to 0$ как $r^l,$ т.е. даже она содержит информацию о величине углового момента $l$

Это был замечательный (и довольно очевидный) ответ на вопрос - где в волновой функции "прячется" модуль (длина) вектора углового момента. Но вопрос был о направлении.

Кстати, если это направление флуктуирует, то есть изменяется со временем (если это допустимо в данном случае перейти от флуктуаций к изменению во времени), то можно ли в КМ (без классической прецессии) явно выразить эту зависимость от времени? Или другими словами - эти флуктуации есть чисто случайный процесс (связанный напр. с измерениями) или их можно представить как некоторое закономерное изменение (вроде классической прецессии).

Cos(x-pi/2) в сообщении #1006952 писал(а):

$\mathbf{\hat l} = -i \mathbf{e}_{\varphi} \frac{\partial}{\partial \theta}+i\mathbf{e}_{\theta} \frac{1}{\sin \theta} \frac{\partial}{\partial \varphi}$

Умножаем слева, справа - получаем плотность. Интегрируем по всему объему атома - получаем (если в.ф. нормирована) собственное значение, число, например 3, как в примерах выше, но не направление.

Возникает ощущение, что до измерения никакого направления $ l $ просто нет вообще. Вероятно, флуктуации относятся к тому, что получится после многократных измерений, но не к заданной волновой функции до измерения.

Можно ли подытожить все таким образом. Направление $ l $, да и сам вектор $ l $ - это предрассудок, оставшийся от древней квазиклассической модели атома. И более адекватно было бы говорить просто о трех собственных значениях, не объединяя все это в классический вектор. Из этих трех собственных значений для двух получаются в эксперименте различные значения, а третье всегда одно и то же (если конечно атом не пинать перед измерением и направление $z$ выбрано правильно)

-- 23.04.2015, 01:01 --

Helium в сообщении #1006960 писал(а):

Prikol в сообщении #1006930 писал(а):

Я еще на второй странице темы пытался "пробить" ТС на какую-либо связь с автором "концепции полей движения".

Действительно я не имею к этому никакого отношения. Но то что разные люди независимо друг от друга пришли к одной мысли, для меня это уже очень сильный сигнал, что тут кое что ценное имеется.

К этой мысли за почти сто лет приходила просто тьма народу. Но в итоге практически все пришли к выводу, что орбитальный момент всетаки лучше оставить целым у более удобоваримым, а менее удобоваримую спиновую составляющую выделить в отдельную компоненту.