Диск Эйнштейна

[Nirowulf]

Раз ушла речь зашла про вложения, позволю и я себе вставить пару слов.

Согласно теореме Жане-Картана $(1926,1927)$ произвольное риманово многообразие размерности $d$ может быть локально изометрически вложено в любое риманово многообразие размерности, большей или равной

$$N=\frac{d(d+1)}{2}.$$

В частности, в плоское пространство такой размерности. В теореме предполагается, что метрика есть аналитическая функция от координат. На случай неопределённой сигнатуры метрики эта теорема была обобщена Фридманом $(1961).$

"Классом вложения" назовём $p=N-d.$ Для $4$-мерного многообразия получаем, что необходимое число измерений плоского объемлющего пространства $N=10,$ а класс вложения равен $6.$
В случае, когда многообразие обладает симметриями, класс вложения может быть понижен. Например, метрика Шварцшильда обладает $SO(3) \times T^1$ симметрией, поэтому оказывается, что её можно вложить в объемлющее пространство всего $6$ измерений. Уменьшить необходимое число измерений объемлющего пространства до $5$ уже не получается. По теореме Казнера $(1921)$ вакуумное решение уравнений Эйнштейна не может быть вложено в $5$-мерное объемлющее пространство.

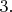
Теперь сформулирую, в общем виде, моё понимание вопроса, вокруг которого развернулась дискуссия. Греческие индексы будут бегать от $0$ до $4,$ латинские $-$ от $1$ до $3.$ Итак, у нас есть $4$-мерное многообразие с метрикой

$$ds^2=g_{\mu \nu}dx^\mu dx^\nu. \eqno (1)$$

Дальше мы по формуле строим из $g_{\mu \nu}$ величину, которую вслед за ЛЛ назовём пространственной метрикой

$$\gamma_{ik}=-g_{ik}+\frac{g_{i 0}g_{k 0}}{g_{00}}. \eqno (2)$$

Тем самым получаем некоторое $3$-мерное многообразие с метрикой

$$dl^2=\gamma_{ik}dx^idx^k. \eqno (3)$$

Можно ли вложить эту метрику в плоское $4$-мерие? Отнюдь. По вышеозначенной теореме минимальное число измерений $N=\frac{3 \cdot 4}{2}=6.$ Но, как мы помним, нас могут выручить симметрии метрики и, возможно, понизить нам необходимое число измерений.

Обратимся к случаю вращения с постоянной скоростью $w$, который тут всё мусолят. Для него метрика пространства-времени есть

$$ds^2=(c^2-w^2r^2)dt^2-2wr^2dtd\varphi-dr^2-r^2d\varphi^2-dz^2, \eqno(4)$$

пространственная метрика

$$dl^2=dr^2+\frac{r^2}{1-\frac{w^2r^2}{c^2}}d\varphi^2+dz^2. \eqno(5)$$

Нетрудно заметить, что пространственная метрика обладает явной цилиндрической симметрией: один поворот в плоскости и одна трансляция. Что даёт надежду на возможность вложения такой метрики в плоское пространство меньшего числа измерений, чем $6.$

Можно ли построить некоторую $3$-мерную метрику, автоматом вложенную в $(1)?$ Да, это известная метрика АДМ:

$$\beta_{ik} \equiv g_{ik}|_{x^0=\operatorname{const}}, \eqno (6)$$

$$\beta^{kl}=\left.(g^{kl}-\frac{g^{k 0}g^{l 0}}{g^{00}})\right|_{x^0=\operatorname{const}}, \eqno (7)$$

$$dl^2_{ADM}=\beta_{ik}dx^idx^k. \eqno (9)$$

Метрика АДМ по определению есть метрика подмногообразия, поэтому автоматом вложено в исходное пространство-время, поэтому для случая вращения метрика АДМ вложена в Минковского.

Пространственная метрика из ЛЛ

$$\gamma_{ik}=-g_{ik}+\frac{g_{i 0}g_{k 0}}{g_{00}},$$

$$\gamma^{kl}=-g^{kl},$$

похожа на метрику АДМ, но не есть оно. В случае вращения это метрика пространства, определяемого условием $\tau=\operatorname{const}$ или $d\tau=0,$ где

$$d\tau=\sqrt{1-\frac{w^2r^2}{c^2}}\left(dt-\frac{wr^2}{c^2(1-\frac{w^2r^2}{c^2})}d\varphi\right).$$

Пространство время с метрикой

$$d\tilde{s}^2=c^2d\tau^2-dl^2=c^2d\tau^2-dr^2-\frac{r^2}{1-\frac{w^2r^2}{c^2}}d\varphi^2-dz^2$$

не есть плоское пространство, в чём можно убедиться, посчитав тензор кривизны.

[Nirowulf]

Nirowulf в сообщении #1002613 писал(а):

определяемого условием $\tau=\operatorname{const}$ или $d\tau=0,$

Прощу прощения, просто условием $d\tau=0,$ ибо это не есть полный дифференциал.

[Munin]

Nirowulf
(4) плоская?

[Nirowulf]

Munin
Так точно.

[epros]

мат-ламер в сообщении #1002604 писал(а):

видим, что в обеих формулах время задаётся одной и той же переменной t. А с чего бы это вдруг?

Да с того, что координатное время вращающейся СО определяют часами, расположенными на оси. А для них без разницы, вращаются они или нет.

мат-ламер в сообщении #1002604 писал(а):

Итак, все часы как вращающейся СО, так и на неподвижной ИСО сохраняют свою синхронность.

Между собой часы вращающейся СО несинхронны. Корректировать скорость хода бесполезно.

[schekn]

epros в сообщении #1002749 писал(а):

Между собой часы вращающейся СО несинхронны. Корректировать скорость хода бесполезно.

Ну почему же. Если на спутнике произошел сбой из-за магнитной бури, то обмениваясь сигналами с эталонными часами , которые покоятся в центре вращения ( которые покоятся относительно инерциальной СО), можно на некоторое время восстановить ход часов. Думаю именно так и делается. Вообще говоря , привязывать определение перехода в другую СО с радарным методом вычисления пространственной геометрии смахивает на альтернативщину, хотя с первого взгляда ничему не противоречит.

-- 11.04.2015, 22:45 --

мат-ламер в сообщении #1002570 писал(а):

Дело в том, что синхронизация часов в пар.84 ЛЛ-2 не совпадает с синхронизацией часов в пар.89. Как я пытался показать на странице 4 темы topic95378-45.html
, метрика Ланжевена из пар.89 возникает, если часы на вращающейся окружности синхронизированы из ИСО внешнего пространства Минковского. Что совпадает с синхронизацией часов из центра. Такая синхронизация возможна в глобальном смысле. Из неё следует, что скорость света в разных направлениях в СО вращ. окружности разная. Часы на вращ. окружности синхронно запаздывают относительно часов ИСО внешнего пространства Минковского. Но если на окружности поставить часы, которые идут убыстренно с одинаковым коэффициентом (понятно каким), то тогда все часы, как на окружности, так и на ИСО во внешнем пространстве Минковского идут синхронно. Такая синхронизация важна для практики и используется в системах глобального позиционирования. Жду от вас аргументированной критики, поскольку в цитируемой ветке на меня сильно наехали, но аргументацию я не понял вообще.

У меня нет возражений по вашему посту. Но У меня вычисления расхождения хода времени часов ,которые делают оборот на некоторой орбите, выполненных радарно с часами , находящимися в центре диска отличается от того, что получается если выполнить по методу ЛЛ-2 в пар. 89 , синхронизируя между близкими часами, расположенными на такой же вращающейся орбите ( кажется в 2 раза), если делать обход по орбите. Если понятно, что я сказал.

[epros]

schekn в сообщении #1002777 писал(а):

можно на некоторое время восстановить ход часов.

Вы о чём? Я про несинхронность часов друг с другом.

schekn в сообщении #1002777 писал(а):

привязывать определение перехода в другую СО с радарным методом вычисления пространственной геометрии смахивает на альтернативщину, хотя с первого взгляда ничему не противоречит.

Какой смысл в системе отсчёта, если не определён способ измерения расстояний? Что отсчитывать?

[schekn]

epros в сообщении #1002800 писал(а):

Какой смысл в системе отсчёта, если не определён способ измерения расстояний? Что отсчитывать?

А Вы его строго точно не определили.
Во-первых, эталонные часы остались в центре диска и они не вращаются. Они калибруются в инерциальной СО. Как они же поведут себя при сильном вращении не очевидно. Если диск раскрутить с большой скоростью, его может и разорвать на части. И часы могут показывать разные величины , в зависимости, где они расположены и как сильно раскручен диск.
Во-вторых, я тут подзабыл, Вы радарным методом получаете 3 величины, общаясь с соседними наблюдателями по 3-м направлениям. Вы сможете по ним однозначно восстановить 3-х мерную геометрию в данном малом объеме?
В-третьих, наблюдателей соседних может и не быть, а переход в другую СО осуществить сможете. Спутник вращается по орбите, а второй наблюдатель остался на Земле.
В-четвертых, если СО неравномерно (ускоренно) вращается, то , как замечено в ЛЛ-2 теряет смысл само понятие пространственного расстояния. Это значит он не перешел в другую неинерциальную СО? А вот в определении Сергея Губанова, такой переход возможен, описывается и ничего в этом страшного нет.

[мат-ламер]

epros в сообщении #1002749 писал(а):

мат-ламер в сообщении #1002604 писал(а):

видим, что в обеих формулах время задаётся одной и той же переменной t. А с чего бы это вдруг?

Да с того, что координатное время вращающейся СО определяют часами, расположенными на оси. А для них без разницы, вращаются они или нет.

мат-ламер в сообщении #1002604 писал(а):

Итак, все часы как вращающейся СО, так и на неподвижной ИСО сохраняют свою синхронность.

Между собой часы вращающейся СО несинхронны. Корректировать скорость хода бесполезно.

По поводу первого вашего предложения

Цитата:

Да с того, что координатное время вращающейся СО определяют часами, расположенными на оси.

Чем часы расположенные на оси выделяются от остальных часов? Тут либо координатное время вращ. СО определяется всеми часами, если они идут синхронно, либо этого времени вообще нет, и можно говорить о координатном времени лишь в какой-то конкретной точке.

По поводу второго.

Цитата:

Между собой часы вращающейся СО несинхронны. Корректировать скорость хода бесполезно.

Если мы возьмём стандартные часы, синхронизируем их в какой-то момент времени, то в дальнейшем часы на окружности большего радиуса будут отставать от часов на окружности меньшего радиуса. И тут трюк состоит в том, что ввести некое эффективное (искусственное) время, состоящий в том, чтобы использовать часы, идущие с разной скоростью. Однако, учитывая вращение, получаем видимый эффект, что все часы идут синхронно и с одинаковой скоростью. Именно для такого искусственного времени и выписана метрика Ланжевена в пар. 89 ЛЛ-2. Если использовать стандартные часы, то метрика будет иметь чуть-чуть другой вид. Всё сказанное есть лишь ИМХО. Может ещё не до конца разобрался.

[epros]

schekn в сообщении #1002868 писал(а):

А Вы его строго точно не определили.

Радаром точно определено.

schekn в сообщении #1002868 писал(а):

Во-первых, эталонные часы остались в центре диска и они не вращаются. Они калибруются в инерциальной СО. Как они же поведут себя при сильном вращении не очевидно. Если диск раскрутить с большой скоростью, его может и разорвать на части.

Фиг знает что несёте.

schekn в сообщении #1002868 писал(а):

Во-вторых, я тут подзабыл, Вы радарным методом получаете 3 величины, общаясь с соседними наблюдателями по 3-м направлениям.

Расстояния измеряются по всем направлениям. Это и означает определить метрику.

schekn в сообщении #1002868 писал(а):

В-четвертых, если СО неравномерно (ускоренно) вращается, то , как замечено в ЛЛ-2 теряет смысл само понятие пространственного расстояния.

Это не совсем так. Просто результат измерения расстояния зависит от времени.

schekn в сообщении #1002868 писал(а):

А вот в определении Сергея Губанова, такой переход возможен, описывается и ничего в этом страшного нет.

У Сергея Губанова нет никакого определения. Впрочем, если судить по той чепухе, которую Вы тут несёте, Вам лучше воздержаться от суждений на эту тему.

-- Вс апр 12, 2015 20:12:55 --

мат-ламер в сообщении #1003072 писал(а):

И тут трюк состоит в том, что ввести некое эффективное (искусственное) время, состоящий в том, чтобы использовать часы, идущие с разной скоростью. Однако, учитывая вращение, получаем видимый эффект, что все часы идут синхронно и с одинаковой скоростью.

Это не называется синхронностью. Координатное время вращающейся системы синхронно по радиусу и несинхронно вдоль окружности.

[мат-ламер]

epros в сообщении #1003114 писал(а):

Координатное время вращающейся системы синхронно по радиусу и несинхронно вдоль окружности.

Во! А я представлял себе ситуацию с точностью до наоборот (если использовать часы, идущие со стандартной скоростью). Т.е. все часы на окружности можно засинхронизировать между собой. Но они будут отставть от часов в центре (внешнем пространстве). Причём скорость запаздывания пропорциональна радиусу окружности. Впрочем я пошёл читать сборник, цитируемый в теме про парадокс Эренфеста. А то может глупости говорю.

[schekn]

epros в сообщении #1003114 писал(а):

Фиг знает что несёте.

epros в сообщении #1003114 писал(а):

У Сергея Губанова нет никакого определения. Впрочем, если судить по той чепухе, которую Вы тут несёте, Вам лучше воздержаться от суждений на эту тему.

Судя по тому , что несете Вы, можно причислить вас к альтернативщикам. И предать анафеме. На форуме любят придерживаться канонам "учебников".
Разве часы , которые находятся в сильном магнитном поле будут идти также , как без него? Точно также не очевидно, что в сильных гравитационных полях они буду идти также как и без гравитации.

У Губанова есть определение, если Вы его не знаете или не понимаете, это Ваша проблема.

-- 12.04.2015, 21:13 --

epros в сообщении #1003114 писал(а):

Расстояния измеряются по всем направлениям. Это и означает определить метрику.

Забыли добавить, что определить можно так метрику в бесконечно малом объеме.

И , кстати не ответили на вопрос, о способе измерения пространственной метрики, если соседних часов не оказалось в наличии.

[epros]

schekn в сообщении #1003145 писал(а):

Судя по тому , что несете Вы, можно причислить вас к альтернативщикам. И предать анафеме. На форуме любят придерживаться канонам "учебников".

У меня-то всё в согласии с учебниками, только Вы их прочесть нормально не можете, поэтому и не видите.

schekn в сообщении #1003145 писал(а):

Забыли добавить, что определить можно так метрику в бесконечно малом объеме.

Метрика определяется в каждой точке.

schekn в сообщении #1003145 писал(а):

И , кстати не ответили на вопрос, о способе измерения пространственной метрики, если соседних часов не оказалось в наличии.

"Если бы часов не оказалось в наличии, то их следовало бы выдумать". А вообще-то для измерения расстояния до чего-либо радаром, там часы не нужны. Достаточно только чтобы сигнал оттуда отражался.

[schekn]

epros в сообщении #1003153 писал(а):

Достаточно только чтобы сигнал оттуда отражался.

Откуда? Если соседа нет в наличии?

-- 12.04.2015, 23:47 --

epros в сообщении #1003153 писал(а):

У меня-то всё в согласии с учебниками, только Вы их прочесть нормально не можете, поэтому и не видите.

Ага, если в одном параграфе определение СО близкое к правильному, а в другом все перековеркано.

[SergeyGubanov]

epros в сообщении #1002432 писал(а):

SergeyGubanov в сообщении #1002385 писал(а):

Синие линии друг от друга строго изолированы.

Что Вы несёте? Синие линии составляют поверхность, но это не та поверхность, которая является решением Вашего уравнения, т.е. она не ортогональ к мировым линиям частей карусели.

Синие линии $x^{\mu}(\ell)$ не составляют поверхность, они ортогональны $e^{(0)}_{\mu}$, являются решением уравнения $e^{(0)}_{\mu} \frac{dx^{\mu}}{d \ell} = 0$.

epros в сообщении #1002432 писал(а):

SergeyGubanov в сообщении #1002385 писал(а):

Вообще-то не линии, а точке

Три пространственные координаты определяют мировую линию.

Три пространственные координаты определяют одну точку пересечения четырёхмерной мировой линии и трёхмерного пространства:

epros в сообщении #1003114 писал(а):

schekn в сообщении #1002868 писал(а):

А вот в определении Сергея Губанова, такой переход возможен, описывается и ничего в этом страшного нет.

У Сергея Губанова нет никакого определения. Впрочем, если судить по той чепухе, которую Вы тут несёте, Вам лучше воздержаться от суждений на эту тему.

Очередная прямя ложь от epros. Частота генерации прямой лжи участником epros увеличивается.

schekn в сообщении #1002868 писал(а):

В-четвертых, если СО неравномерно (ускоренно) вращается, то , как замечено в ЛЛ-2 теряет смысл само понятие пространственного расстояния. Это значит он не перешел в другую неинерциальную СО? А вот в определении Сергея Губанова, такой переход возможен, описывается и ничего в этом страшного нет.

Они привязали систему координат к системе отсчёта формулой $e^{(0)}_{\mu} = g_{0 \mu} / \sqrt{g_{00}}$. Но группа преобразований координат четырёх пераметрическая, а группа вращений тетрады шести параметрическая. То есть различных систем отсчёта "сильно больше" чем систем координат. Поэтому не удивительно, что порой чего-то привязанное к системе координат "теряет смысл".

Кстати, пространственные расстояния (точнее длины пространственно подобных линий) задаваемые тетрадой по определению являются радарными. Смысл дифференциальной формы $e^{(0)} = e^{(0)}_{\mu} dx^{\mu}$ - это бесконечно малый элемент времени. Смысл трёх дифференциальных форм $e^{(i)} = e^{(i)}_{\mu} dx^{\mu}$ - это бесконечно малые элементы длины вдоль трёх ортогональных пространственных направлений. Радарность тетрадных бесконечно малых элементов длины:

$$ ds^2 = \eta_{(a)(b)} e^{(a)} e^{(b)} = \left( e^{(0)} \right)^2 - \left( e^{(1)} \right)^2 - \left( e^{(2)} \right)^2 - \left( e^{(3)} \right)^2. $$

мат-ламер в сообщении #1002570 писал(а):

Такая синхронизация важна для практики и используется в системах глобального позиционирования.

Синхронизация часов вещь конечно интересная, но так сказать бытовая, "дело хозяйское". На расстояния (на длины пространственно подобных линий) равно как и на промежутки времени (длины времениподобных линий) синхронизация часов никак не влияет. Длины четырёхмерных линий "объективно существуют" сами по себе, а методы синхронизации конкретных часов - сами по себе.