А если "наблюдатель" сам 10 раз, помолясь, прошёл между Сциллой и Харибдой? А если в его выборке и нет больше никаких наблюдений? Что получим?
А в этом случае вы не можете выкинуть
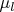
. Более интересно
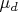
. Так как
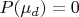
по определению понятия "наблюдатель", никакие

не определены, и вы не можете с ними записывать какие-либо выражения, в том числе, пытаться воспользоваться формулой Байеса с ними.
Пример расчёта можете привести?
Вот, скажем, при

все четыре варианта считаем равновероятными:
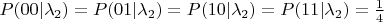
, где первый нуль или единица означают "не молился" или "помолился", а второй нуль или единица означают "не выжил" или "выжил". При

считаем, что вероятности для первых двух случаев (т.е. когда "не молился") остаются теми же, а вероятность для "помолился и не выжил" обнуляется:
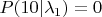
. Стало быть вероятность для "помолился и выжил" возрастает до
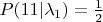
. Допустим, что априорные вероятности гипотез тоже равны:
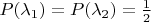
.
Я так понимаю, что если наблюдатель 10 раз помолился и выжил, и другой статистики у него нет, то по Вашей методике расчёта мы первое, что должны сделать, это выкинуть (обнулить) все случаи "не выжил". В итоге останутся:
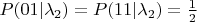
,
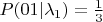
и
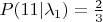
. По формуле Байеса получим апостериорную вероятность

, равную
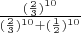
(около 95%).
Или у Вас другая методика?