Психическая причинность

[Formalizator]

warlock66613 в сообщении #1717739 писал(а):

Чалмерс доказывает, что физическая модель ментального принципиально невозможна.

Которую систему понятий использует Чалмерс в том «доказательстве»? Разве Чалмерс доказывает тот тезис?

[realeugene]

epros в сообщении #1717745 писал(а):

Или у Вас другая методика?

Сначала попытаюсь разобраться в вашей. Обозначения нехорошие. $\lambda_1$ и $\lambda_2$ утонуло в теме. Уже не помню что они обозначают. Полезно их переименовать. Обозначение событий цифрами вообще ужасно. Пусть будет для событий выживания $\mu_+$ и $\mu_-$, а для событий молитвы $p_+$ и $p_-$. Сейчас спешу, разберусь позже. Можете переименовать и подчистить свой вывод? В результате не останется безусловной вероятности $P(\lambda_x)$. Вы не можете избавиться от $\mu_x$ по Байесу. Так что все мелкие шаги, которые вы делаете, важны - вы где-то ошибаетесь.

[warlock66613]

Formalizator в сообщении #1717746 писал(а):

Которую систему понятий использует Чалмерс в том «доказательстве»? Разве Чалмерс доказывает тот тезис?

Я без понятия что такое "система понятий" и какой "тот" тезис вы имеете в виду.

[b4b5]

warlock66613 в сообщении #1717742 писал(а):

Небольшие целые числа -- это не совсем ментальные объекты, это абстрактные объекты.

Тогда любые абстракции - ментальные объекты, по вашему.

[realeugene]

epros в сообщении #1717745 писал(а):

$\frac{(\frac{2}{3})^{10}}{(\frac{2}{3})^{10}+(\frac{1}{2})^{10}}$

И просто в степень возводить нельзя, так как события выживания в разные проходе не являются независимыми. Условие выживания одно - выжил в конце, когда оценивается вероятность.

И подозреваю, что если у каждого испытания возможен только один исход, то апостериорные вероятности гипотез равны априорным. Получаемая информация равна нулю.

[b4b5]

По поводу молитвы и гибели.
Оба имеют одинаковый риск погибнуть. Разница только в объяснении только. )
Предположим, было 10 экспериментов и оба выжили.
Человек без молитвы заключает «вероятность гибели маленькая».
Человек с молитвой заключает «вероятность гибели маленькая или молитва существенно снижает вероятность гибели».

Поскольку тут не различить гипотезы, то в данном эксперименте гипотеза о работе молитвы будет подобна высказыванию «очередная философская гипотеза без фальсификации», которыми эта тема переполнена. ))

[epros]

realeugene в сообщении #1717751 писал(а):

события выживания в разные проходе не являются независимыми

Независимые разумеется.

realeugene в сообщении #1717751 писал(а):

И подозреваю, что если у каждого испытания возможен только один исход, то апостериорные вероятности гипотез равны априорным. Получаемая информация равна нулю.

Жесть. По Вашей логике, похоже, вообще у всех событий во Вселенной может быть только один исход: могло произойти только то, что произошло? Байесовскую оценку вообще выкидываем?

-- Вс фев 08, 2026 20:38:30 --

b4b5 в сообщении #1717756 писал(а):

Оба имеют одинаковый риск погибнуть.

Оба это кто? Я предложил такие вероятности, что молящихся примерно половина. Но почему-то оказалось, что выборка у нас только для одного человека ("наблюдателя"), который оказался молящимся.

[b4b5]

Возможно я плохо вчитывался, я так понял задачу, ошибка выжившего + молитва.
--
Сценарий, человек делает тест на выживание, открывает коробку в которой может быть яд или может не быть яда. Коробок бесконечно много.
Вероятность того, что в коробке есть яд неизвестна.

Первый открывает последовательно N коробок, остается живой.
Второй открывает последовательно N коробок, остается живой.
Второй перед открытием коробки принимает лекарство, которое может быть плацебо, а может быть антидотом к яду, вероятность того, что там плацебо неизвестна.

Надо для Первого построить модель, вычислить вероятность выживания для коробки N+1.
Надо для Второго построить модель, вычислить вероятность выживания для коробки N+1.
--

[realeugene]

epros в сообщении #1717757 писал(а):

Независимые разумеется.

Разумеется, они зависимы: выжить или погибнуть на пятом проходе можно только если выжил на предыдущих четырёх. Но тут важно определить вероятностное пространство, чтобы посчитать всё аккуратно.

epros в сообщении #1717757 писал(а):

По Вашей логике, похоже, вообще у всех событий во Вселенной может быть только один исход: могло произойти только то, что произошло? Байесовскую оценку вообще выкидываем?

Нет, конечно. Но если в вероятностном пространстве только одно событие, то и байесовская оценка ничего не изменяет.

-- 08.02.2026, 20:39 --

epros в сообщении #1717757 писал(а):

Но почему-то оказалось, что выборка у нас только для одного человека ("наблюдателя"), который оказался молящимся.

Сначала можно расписать для наблюдателя за наблюдателем. А потом сузить к оценке самим наблюдателем.

[realeugene]

epros в сообщении #1717745 писал(а):

Или у Вас другая методика?

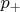
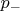
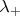
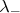
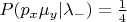
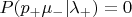
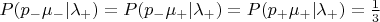
События такие: $p_+$ - молился, $p_-$ - не молился, $\mu_+$ - выжил, $\mu_-$ - погиб, $\lambda_+$ - молитва спасает, $\lambda_-$ - молитва бесполезна. Вы задаёте следующие вероятности: $P(p_x\mu_y|\lambda_-) = \frac 1 4$, $P(p_+\mu_-|\lambda_+) = 0$, $P(p_-\mu_-|\lambda_+) = P(p_-\mu_+|\lambda_+) = P(p_+\mu_+|\lambda_+) = \frac 1 3$. Свободные переменные пробегают $+$ и $-$.

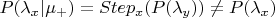
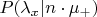
Пусть делается один проход. Если смотреть со стороны, апостериорные вероятности можно посчитать по Байесу, считать точно не буду, не важно, но скорее всего апостериорные вероятности после успешного прохода будут отличаться от априорных: $P(\lambda_x|\mu_+) = Step_x(P(\lambda_y))\ne P(\lambda_x)$. Чтобы посчитать апостериорную вероятность $P(\lambda_x|n\cdot\mu_+)$ после $n$ успешных проходов, нужно апостериорную вероятность вычислить рекурсивно: $P(\lambda_x|n\cdot\mu_+) = Step_x(P(\lambda_y|(n-1)\cdot\mu_+))$.

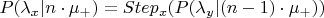
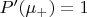
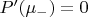
Теперь посмотрим, что происходит, когда вероятности должен оценивать сам наблюдатель на корабле. Так как он сам наблюдатель, то если он знает достоверно, что он выжил: $P'(\mu_+) = 1$, $P'(\mu_-) = 0$. По Байесу в лоб считать не получится. Сначала нужно вычислить все вероятности кроме априорных при условии того, что наблюдатель выжил. 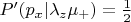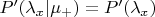Имеем $P'(p_x\mu_y|\lambda_z\mu_+)=\frac 1 2 [y=+]$, откуда $P'(p_x|\lambda_z\mu_+)=\frac 1 2$, откуда легко по Байесу получаем, что $P'(\lambda_x|\mu_+) = P'(\lambda_x)$, а значит, $P'(\lambda_x|n\cdot\mu_+) = P'(\lambda_x)$. 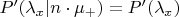Сколько ни ходи между скалами сам, но факт твоего выживания никак на апостериорные вероятности гипотез не влияет, они остаются равными априорным.

[b4b5]

Кстати, ошибку выжившего на мой взгляд правильно стоит трактовать как задачу найти вероятность восхода солнца от Лапласа. )

[realeugene]

b4b5 в сообщении #1717773 писал(а):

Кстати, ошибку выжившего на мой взгляд правильно стоит трактовать как задачу найти вероятность восхода солнца от Лапласа. )

Это как?

[b4b5]

realeugene Какова вероятность того, что солнце взойдет завтра, если мы наблюдали N восходов. Кажется так формулируется.

[realeugene]

realeugene в сообщении #1717771 писал(а):

откуда легко по Байесу получаем, что $P'(\lambda_x|\mu_+) = P'(\lambda_x)$

На самом деле это неверно. Байеса там уже применять нельзя, так как в нём нужно знать $P(\lambda_x|\mu_+)$, которые мы и хотим узнать. А так как все вероятности становятся условными с условием $\mu_+$, получается тривиальное тождество $P(\lambda_x|\mu_+) = P(\lambda_x|\mu_+)$.

[epros]

realeugene в сообщении #1717761 писал(а):

Разумеется, они зависимы: выжить или погибнуть на пятом проходе можно только если выжил на предыдущих четырёх.

Разумеется независимы. Результаты пятого забега через Сциллу и Харибду не зависят от того, что было бы, если бы клиент участвовал в первых четырёх забегах.

realeugene в сообщении #1717761 писал(а):

если в вероятностном пространстве только одно событие

Это как? Где здесь только одно событие?

Я Вам вначале написал, как делается нормальное Байесовское оценивание: рассматривается максимально репрезентативная выборка, включающая и тех, кто не выжил, и тех, кто не молился. И правильная оценка гипотезы "молившийся точно выживет" появится, как только в выборку попадёт хотя бы один не выживший молившийся, ибо по формуле апостериорная вероятность этой гипотезы сразу обнулится. А тот вариант, когда мы ограничиваем выборку только выжившими, и называется ошибкой выжившего.

Вообще странно, что с Вашей подачи мы тут вынуждены обсуждать не относящийся к теме вопрос о том, нужно ли включать во все теории эту дурацкую аксиому "я существую".