Someone Нет, не получается, наверное стоит остановится и вернутся когда-нибудь потом.
Была идея такая:
1. Выделить в

подмножество несократимых кратных

, т.е.
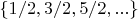
. Этому подмножеству поставить в соответствие подмножество

несократимых кратных с двойкой в степени знаменателя элементов из подмножества

минус один, ну то есть, в данном случае такое же множество.
2. Выделить в

подмножество несократимых кратных

, т.е.
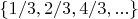
. Этому подмножеству поставить в соответствие подмножество

несократимых кратных с двойкой в степени знаменателя элементов из подмножества

минус один, то есть
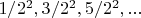
.
3. И т.д.
Формульно это получается похожим на то что, я выводил ранее:
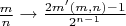
, где
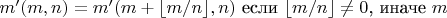
, но это также не монотонно.
Ещё была идея (идея выше это её развитие) как в примере Кантора везде не плотного несчётного множества взять сначала например в интервале

из

точку посередине, тем самым разбив интервал пополам, потом в половинах точку посередине и т.д. И точкам этим сопоставлять как-то точки из

. Ну в частности если из разбиваемого интервала

из

брать всегда точки "слева", то это будут точки
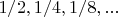
- т.е. как раз степени двойки в знаменателе как в

, только с единичным числителем. Ну вот я и думал как это можно монотонно сделать и пришёл к варианту выше.
Ну, Лектор объясняя пример Кантора вообще отмечал, что выкидывая отрезки (а там отрезок на три части делится, а не на две, но средний выбрасывается), выбирая "левый" или "правый", и в конечном итоге получим систему вложенных отрезков, пересечение которых, как известно - точка, можно как бы представить эту точку таким образом в двоичном виде, на основании выбора левого или правого отрезка на каждой итерации. Не знаю, может это как-то нужно было использовать, и вообще может это задача на пример Кантора, а не теорему, которую Вы упомянули, но я уже устал, поэтому пропускаю.
По-поводу Ваших советов: Вы предлагаете вместо построения одной биекции (что Вы называете "морочить голову"), построить три -
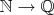
,
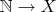
и дальше ещё их композицию что ли. Не знаю как может быть проще вывести формулу "настоящей" биекции натуральных на рациональные, то есть учитывающую сократимые пары

, чем сразу делать биекцию
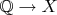
.
(Оффтоп)
не уверен что пункт 2.2 можно выполнить на ограниченном множестве
Нет, конечно можно, просто на ограниченном множестве последовательность элементов такого подмножества, всегда будет фундаментальной. Подмножество также будет (как в случае ограниченного так и не ограниченного) замкнутым
(Оффтоп)
второе, что Вам нужно сделать — доказать, что множество

счётно, и что в нём нет щелей, а также первого и последнего элементов (предположим, что про

мы это знаем, но можно и доказать)
Чтобы не приостанавливать на такой грустной ноте, докажу хотя бы что в

нет скачков (чисто алгебраически) и что оно счётно:
1.1.
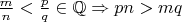
,
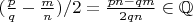
.
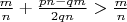
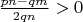
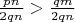
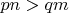
1.2
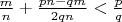
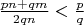
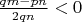
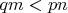
Для

аналогичо.
Счётность

: представим

(положительную часть) как таблицу

, в ячейках которой рациональные числа определяющиеся парой

как

, и в которой учтены повторы за счёт сокращающихся дробей.
Нужно натуральные числа поставить в соответствие счётному числу элементов в каждой из счётного числа строк. На каждую

-ую строку в

выделим подмножество всех степеней

-го простого числа, то есть, например на вторую строку - степени первого простого числа - двойки, на третью - второго - тройки, на четвёртую строку - третьего простого числа - пятёрки.
Поскольку простых чисел счётно(бесконечно), то на каждую строку найдётся множество степеней простого числа, причём однозначно. Поскольку степени простого числа - натуральные числа, множество которых счётно, то на каждый столбец каждой строки найдётся конечное натуральное число, при чём однозначно, поскольку множества степеней разных простых чисел не пересекаются, в силу Основной Теоремы Арифметики (единственности факторизации, в частности).
В

остаются составные числа. Их также счётно. Сопоставим их всех, кроме первого однозначно элементам первой строки таблицы

; первый сопоставим нулю из

. Для того чтобы учесть отрицательные - в каждой строке сопоставляем не все степени

-го простого, а только: чётные - для положительных, нечётные для отрицательных. Для первой строки для отрицательных логика та же, только без сдвига на один элемент