Да я наоборот до этого всё подробно и расписывал
Просто мне приходится догадываться. И это еще полбеды, но может оказаться так, что Вы имели в виду что-то неправильное, а я додумаю правильное, и тогда весь смысл упражнения пропадает.
Это реально можно было решить за 30 минут (или сколько там) коллоквиума, при том что есть как бы другие задачи? Это первый модуль первого семестра же
А Вы самостоятельно предмет изучаете, или в университете?
В университете должны быть еще и семинары, где подробно объясняют подобные вещи. Тут вся задача на стандартные техники, но к ним нужно привыкнуть.
Ага, построили монотонную инъекцию
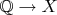
. Но она не обязана быть сюръекцией. Чтобы была, надо строить несколько иначе - на каждом шаге следить, чтобы очередная функция была определена на

, и при этом

было в образе.