Биекция мн. чисел вида (m/2^n), m,n-Z во мн.Q возрастающая?

[cxzbsdhwert]

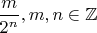
Есть задача - доказать существование возрастающей биекции множества чисел вида $\dfrac{m}{2^n},\space m,n \in \mathbb{Z}$ в множество рациональных чисел $\mathbb{Q}$.

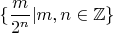
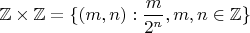
Биекцию, как таковую, могу доказать исходя из того, что $\mathbb{Q}$ - счётно (по диагональному аргументу Кантора), а множество чисел $\{\dfrac{m}{2^n}|\space m,n \in \mathbb{Z}\}$, наверное стоит представить в виде Декартова произведения $\mathbb{Z}\times\mathbb{Z}=\{(m,n):\dfrac{m}{2^n},\space m,n \in \mathbb{Z}\}$, $\mathbb{Z}$ счётно (биекция из $\mathbb{N}$ по принципу: чётные - положительные целые, нечётные, кроме единицы - отрицательные целые, единица - ноль), а декартово произведение счётных множеств является счётным множеством (дольше доказывать, ну по диагонали короче биекция).
Тогда получаем множество чисел указанного выше вида - счётное множество, $\mathbb{Q}$ - тоже счётное множество, значит они равномощны, значит есть биекция между ними.

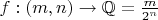
Я не понял только почему $f:(m,n)\rightarrow \mathbb{Q}=\frac{m}{2^n}$ возрастающая.
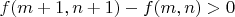
Нужно наверное показать, что $f(m+1,n+1)-f(m,n)>0$, но это очевидно не так. По отдельности? Но почему по отдельности? Если только $m$ инкрементировать, то будет возрастающая, если только $n$ то будет убывающая, если и $m$ и $n$ то убывающая - при одинаковом приросте аргумента, очевидно $2^x$ растёт быстрее чем $x$, ну, по крайней мере для натурального $x$.

[dgwuqtj]

Начнём с того, что отображение $\mathbb Z \times \mathbb Z \to \{\frac m {2^n} \mid m, n \in \mathbb Z\}, (m, n) \mapsto \frac m {2^n}$ не является биекцией. Например, оно отображает $(1, 0)$ и $(2, 1)$ в число $1$.

[Someone]

cxzbsdhwert в сообщении #1695435 писал(а):

Есть задача - доказать существование возрастающей биекции множества чисел вида $\dfrac{m}{2^n},\space m,n \in \mathbb{Z}$ в множество рациональных чисел $\mathbb{Q}$.

Первое, что нужно сделать — это уточнить определение множества $A=\{\dfrac{m}{2^n}|m,n\in\mathbb{Z}\}$ так, чтобы не было повторов, о чём Вам написал dgwuqtj.

Далее есть общая теорема: Любые два линейно упорядоченных счётных (предполагается, бесконечных) множества без щелей и без первого и последнего элемента подобны.

Щелью в линейно упорядоченном множестве называется пара элементов, между которыми нет других элементов.
Подобием линейно упорядоченных множеств называется возрастающая биекция одного на другое.

Как я понимаю, Вам нужно воспроизвести доказательство этой теоремы на примере множеств $A$ и $\mathbb Q$.
Значит, второе, что Вам нужно сделать — доказать, что множество $A$ счётно, и что в нём нет щелей, а также первого и последнего элементов (предположим, что про $\mathbb Q$ мы это знаем, но можно и доказать).

Далее можно начинать доказательство. Перенумеруем все элементы множеств $A$ и $\mathbb Q$ натуральными числами (без повторений). Затем поочерёдно берём элементы из $A$ и из $\mathbb Q$ и решаем, какой элемент другого множества им сопоставить, чтобы получилась возрастающая биекция.

Над деталями подумайте сами.

Кстати, почему $A\neq\mathbb Q$?

[cxzbsdhwert]

Someone в сообщении #1695441 писал(а):

cxzbsdhwert в сообщении #1695435 писал(а):

Есть задача - доказать существование возрастающей биекции множества чисел вида $\dfrac{m}{2^n},\space m,n \in \mathbb{Z}$ в множество рациональных чисел $\mathbb{Q}$.

Первое, что нужно сделать — это уточнить определение множества $A=\{\dfrac{m}{2^n}|m,n\in\mathbb{Z}\}$ так, чтобы не было повторов, о чём Вам написал dgwuqtj.

1. Произвести уточнение в рамках решения? Или уточнить - в смысле изменить условие задачи, то есть с таким условием функция не биективна?

Цитата:

нет щелей, а также первого и последнего элементов (предположим, что про $\mathbb Q$ мы это знаем, но можно и доказать).

2. Это аксиома полноты? Между двумя любыми подмножествами $A$ и $B$ множества $\mathbb R$, такими что $(\forall a\in A)$ $\leq$ $(\forall b\in B)$ существует элемент $x\in \mathbb R$, то есть $\text{max}(A) \leq x \leq \text{min}(B)$.
Но для $\mathbb Q$ она же не выполняется.
Наибольшего в $\mathbb Q$ нет, наверное потому что оно счётно, содержит в себе $\mathbb N$, а значит по аксиоме Архимеда оно не ограничено сверху, то есть наибольшего нет. Наименьшего нет, наверное потому что отрицательные числа вводятся путём дублирования натуральных с добавлением отрицательного знака, то есть там логика такая-же, только в обратную сторону - то есть $\mathbb Q$ неограниченно снизу, наименьшего элемента нет.

3. $A$, это же всё равно Декартово произведение или что-то подобное, в виду двух переменных, да? То есть элементы $A$ это в любом случае не числа, а пары или что-нибудь такое?

[Shadow]

$Q^+: \quad 2^a \cdot p_1^{b_1}\cdot p_2^{b_2}\ldots p_n^{b_n},\quad a,b_i \in \mathbb{Z}, b_i \ne 0$

Опишите $A^+$ и сделайте биекцию.

[dgwuqtj]

1. У вас же условие задачи уже дано, его менять нельзя. Могу только сказать, что задача корректно поставлена, требуемое утверждение действительно можно доказать.
2. Нет, читайте внимательнее, что такое щель.
3. Нет, по определению $A \subseteq \mathbb Q$, оно состоит из каких-то рациональных чисел. Это как если бы вы утверждали, что $\{2^a 3^b \mid a, b \in \mathbb N\}$ является множеством пар (нет, это множество состоит из натуральных чисел).

[Shadow]

(Оффтоп)

dgwuqtj, простите, я не понял точки 1. 2. 3. к каким вопросам относятся.

[dgwuqtj]

(Оффтоп)

Shadow, это я отвечал на вопросы cxzbsdhwert.

[Shadow]

(Оффтоп)

dgwuqtj, я понял. Просто не увидел последнее сообщение cxzbsdhwert

[cxzbsdhwert]

dgwuqtj в сообщении #1695452 писал(а):

1. У вас же условие задачи уже дано, его менять нельзя. Могу только сказать, что задача корректно поставлена, требуемое утверждение действительно можно доказать.
2. Нет, читайте внимательнее, что такое щель.
3. Нет, по определению $A \subseteq \mathbb Q$, оно состоит из каких-то рациональных чисел. Это как если бы вы утверждали, что $\{2^a 3^b \mid a, b \in \mathbb N\}$ является множеством пар (нет, это множество состоит из натуральных чисел).

2. Пара элементов между которыми нет элемента предъявляется за счёт аксиомы полноты, а точнее неполноты $\mathbb Q$ на банальном, как я понимаю, примере: пусть $A=\{x\in \mathbb Q: x^2 \leq 2 \}$ и $B=\{x\in \mathbb Q: x^2 \geq 2 \}$ тогда пара $(a,b)$ - "щель", такая что $a=\text{max}(A)$, $a=\text{min}(B)$
Вот временная метка лекции, где лектор буквально это утверждает: "В КУ есть дырки".

3. Нет, ну понятно, что это в итоге числа, и следовательно множество чисел, просто, по крайней мере, представлять его ведь можно в виде Декартового произведения ($\mathbb Q$ или множество из задачи).

[dgwuqtj]

2. Вот теперь доказывайте, что у вашего $A = \{x \in \mathbb Q \mid x^2 \leq 2\}$ есть максимальный элемент $a = \max(A)$... Потому что я считаю, что там максимума нет и ваша запись бессмысленна.

Кстати, в $\mathbb Z$ (и даже в $\{0, 1\}$) есть щели в смысле определения Someone, но оно полное.

3. Так биекции же нет! Это вам надо тогда строить отображение $\mathbb Z \times \mathbb Z \to \mathbb Q$, доказывать его сюръективность, потом доказывать, что склеиваются ровно те пары, которые склеиваются при отображении $\mathbb Z \times \mathbb Z \to A$, а потом уже проверять сохранение порядка. При том, что на $\mathbb Z \times \mathbb Z$ берётся не абы какой порядок, а предпорядок, поднятый с $A$ (и он не будет поряком!).

[mihaild]

cxzbsdhwert в сообщении #1695462 писал(а):

тогда пара $(a,b)$ - "щель", такая что $a=\max(A)$,

Так в $A$ нет максимального элемента, что такое $a$?
Вообще, элементы $\mathbb Q$ - это рациональные числа. Можете написать два (не совпадающих) рациональных числа таких, что между ними нет третьего?

Полнота и отсутствие щелей (так же называемое плотностью порядка) - разные вещи. $\mathbb Q$ неполно, но в нём нет щелей. $\mathbb Z$ полно, но в нём есть щели. $\mathbb R$ и полно, и щелей в нём нет. Общепринятых примеров, когда неполно, а щели есть, я не знаю, но строится элементарно.

cxzbsdhwert в сообщении #1695462 писал(а):

Нет, ну понятно, что это в итоге числа, и следовательно множество чисел, просто, по крайней мере, представлять его ведь можно в виде Декартового произведения

Можно, но вряд ли это поможет. С учетом того, что представление должно быть таким, чтобы разным парам из декартова произведения соответствовали разные элементы нашего множества.

[cxzbsdhwert]

dgwuqtj в сообщении #1695464 писал(а):

2. Вот теперь доказывайте, что у вашего $A = \{x \in \mathbb Q \mid x^2 \leq 2\}$ есть максимальный элемент $a = \max(A)$... Потому что я считаю, что там максимума нет и ваша запись бессмысленна.

Кстати, в $\mathbb Z$ (и даже в $\{0, 1\}$) есть щели в смысле определения Someone, но оно полное.

3. Так биекции же нет! Это вам надо тогда строить отображение $\mathbb Z \times \mathbb Z \to \mathbb Q$, доказывать его сюръективность, потом доказывать, что склеиваются ровно те пары, которые склеиваются при отображении $\mathbb Z \times \mathbb Z \to A$, а потом уже проверять сохранение порядка. При том, что на $\mathbb Z \times \mathbb Z$ берётся не абы какой порядок, а предпорядок, поднятый с $A$ (и он не будет поряком!).

2. Ну понятно в общем. "Дырки" в контексте аксиомы полноты есть, "щелей" нет.
Да, о том что на $\mathbb Z$ выполняется аксиома полноты не думал, спасибо.

3. Ну да, не подумал, что при $f: \mathbb Z \times \mathbb Z \rightarrow \mathbb Q\space = \space (m,n)\rightarrow \frac{m}{n}$, не инъекции из-за пар типа $(km,kn)$.

А что Вы буквально имеете в виду под сохранением порядка? Типо чтобы после биекции $A\rightarrow \mathbb Q$ те же элементы $A$ составляли те же классы эквивалентности заданного теперь на $\mathbb Q$ отношения порядка?

[dgwuqtj]

cxzbsdhwert в сообщении #1695470 писал(а):

А что Вы буквально имеете в виду под сохранением порядка? Типо чтобы после биекции $A\rightarrow \mathbb Q$ те же элементы $A$ составляли те же классы эквивалентности заданного теперь на $\mathbb Q$ отношения порядка?

При чём тут классы эквивалентности? По определению, отображение $f \colon X \to Y$ сохраняет порядок, если из $x_1 \leq x_2$ следует $f(x_1) \leq f(x_2)$.

[cxzbsdhwert]

dgwuqtj в сообщении #1695471 писал(а):

cxzbsdhwert в сообщении #1695470 писал(а):

А что Вы буквально имеете в виду под сохранением порядка? Типо чтобы после биекции $A\rightarrow \mathbb Q$ те же элементы $A$ составляли те же классы эквивалентности заданного теперь на $\mathbb Q$ отношения порядка?

При чём тут классы эквивалентности? По определению, отображение $f \colon X \to Y$ сохраняет порядок, если из $x_1 \leq x_2$ следует $f(x_1) \leq f(x_2)$.

Когда мы задаём отображение из множества на котором определён линейный порядок в множество, на котором также определён линейный порядок, элементы $y\in f(D(f))$ области значений отображения должны образовывать отношение порядка $(y_1, y_2)$, где $y_1=f(x_1)$ и $y_2=f(x_2)$ такие что $f(x_1)\leq f(x_2)$.

У нас такое отношение на $\mathbb Q$ после биекции из $A$. Я думал, что имеется в виду, что если мы сначала $A$ отображаем в $\mathbb Z \times \mathbb Z$, а потом уже $\mathbb Z \times \mathbb Z$ отображаем в $\mathbb Q$, то сначала на $\mathbb Z \times \mathbb Z$ должно быть отношение порядка, согласующееся с порядком $A$, и потом это отношение порядка также должно быть сохранено при переносе на $\mathbb Q$.

$A\rightarrow \mathbb Z \times \mathbb Z$. В то же время, на $A$ есть отношение порядка. Каждая пара отношения порядка $(a_1, a_2)$ на $A$, такая что $a_1\leq a_2$ отображается на пару пар отношения порядка на $\mathbb Z \times \mathbb Z$ - $((m_1,n_1),(m_2,n_2))$, такая что $(m_1,n_1)\leq(m_2,n_2)$ и между парами $(m_1,n_1)$ и $(m_2,n_2)$ в свою очередь однозначное соответствие с некоторыми $a_1$ и $a_2$ из $A$, ну и дальше это должно сохраниться на пары отношения порядка на $\mathbb Q$ по такой же логике.

То есть чтобы из пар отношения порядка на $\mathbb Q$ можно было однозначно, через $\mathbb Z \times \mathbb Z$ вернуться на пару отношений порядка на $A$.