Тогда надо доказывать, что любое число из

представляется в таком виде единственным способом. Что неправда, потому что
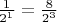
.
Там никаких степеней (кроме 1) в знаменателе нет, оно же сокращается
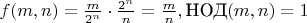
В вашем примере, где слева в равенстве к качестве прообраза (аргумента) пара

это

а справа

, равенства между их образами нет, поскольку
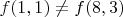
, т.к.
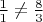
Можно так определять, чтобы более ясно было, что это функция из

.
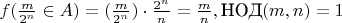
Тут в любом случае сложная функция, и внутренняя - от двух переменных.
То есть берём каждое число из

, например

или
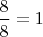
из Вашего сообщения, и множим каждое такое число из

на дробь.
Только дробь эта зависит от того, на какое число её множим. То есть не одну и ту же дробь на каждое из

умножаем, а в зависимости от того что за элемент из

.
Ну а элемент из

определяется, в свою очередь, по условию задачи, парой целых

, следовательно и множитель, в конечном итоге от

зависит и вся биекция.