Хорошо, я правильно понимаю, что мне нужно предъявить новую функцию

, аргументом которой будет

и я с этим

могу всё-что хочу в функции делать алгебраически и более обще - логически?
Именно - аргументом должно быть такое число. А не представление.
Возвращаясь к задаче, мне всё-таки видится некоторая противоречивость: ну вот например Э.Ландау "Основы математического анализа", ст.57 - "Под рациональным числом понимаем совокупность всех дробей, эквивалентных некоторой фиксированной, т.е. класс эквивалентности". Как вообще можно говорить о рациональном числе, во всяком случае нецелом ограничиваясь каким-то одним асболютным объектом?

- это "пять десятых", т.е. используются всё равно пара чисел - т.е. представление.
Значит рациональное число это всё-таки пара чисел.
1. Я вот так и не понял, не могли бы Вы объяснить верно ли сказать, что "число вида

" определяется парой чисел

? Тут проблема в том что и про рациональное число не такого вида можно сказать что оно определяется парой при чём таких же чисел, но при этом это будет другое число.
2.
приведенная
параметризация этого множества - не биективна, разным парам

могут соответствовать одинаковые элементы множества
Два рациональных числа

,

эквивалентны (равны), если

.
Вот здесь и проблема: делаем так чтобы разным парам-прообразам соответствовал один образ - не получается инъекция с точки зрения функции. Делаем разным парам-прообразам разные образы - формально функция инъективна, но в контексте того, что эти разные пары-прообразы - одно рациональное число, получаем что одно число ставится в соответствие разным числам из

. И так не так и так не так
Здесь ранее писали что для достижения инъективности нужно ограничиться рассмотрением взаимопростыми числителями и знаменателями. Но определение инъективной

это
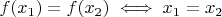
. Почему я не могу сказать что для

, где

,

мн-ва пар,
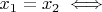
они эквивалентны, как определено выше?
3. Если первый вопрос - да, то можно ли, выбирая путь ограничения по НОД, дополнительно ограничивая

(*) задать биекцию просто
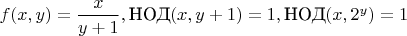
Ну или если ответ нет, то
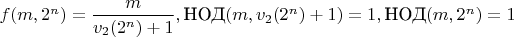
, где
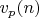
-степень, с которой простое

входит в разложение на простые множители

(ну или просто
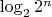
)?
(Оффтоп)
(*) мн-во чисел такого вида с такими ограничениями всё равно то же, поскольку из
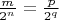
следует существование

и
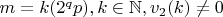
для любых

и
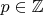
:
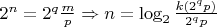
(

перенёс в знаменатель из предположения о

)