Биекция мн. чисел вида (m/2^n), m,n-Z во мн.Q возрастающая?

[cxzbsdhwert]

mihaild в сообщении #1716446 писал(а):

Докажите, что так занумеровать $\mathbb Q$ невозможно.

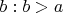
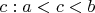
Невозможно потому что задав $b: b>a$ вторым после первого — $a$, найдётся $c:a<c<b$, которому по сюрьективности тоже нужно сопоставить натуральное число большее двух ($1$ и $2$ же уже заняты $a$ и $b$ соответственно) — того натурального числа ($2$), которому соответствует $b$, которого оно меньше. Получается что $c$ меньше $b$, но его номер больше номера $b$

mihaild в сообщении #1716446 писал(а):

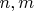
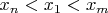
из объявленных свойств следует, что для некоторых $n, m$ выполнено $x_n < x_1 < x_m$ (докажите, что это так).

Раз там нет наименьшего (первого) элемента, то для любого элемента, в том числе того, который будет биекцией занумерован как первый, найдётся меньше его, а по причине того что нет наибольшего, найдётся и больший.

mihaild в сообщении #1716446 писал(а):

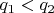
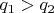
мы хотим куда-то отправить $q_2$ так, чтобы если $q_1 < q_2$, то его образ был больше $x_1$, а если $q_1 > q_2$, то меньше.

С учётом ограничений и той степени общности которую мы рассматриваем я нахожу только такой ответ:

cxzbsdhwert в сообщении #1716444 писал(а):

ставим в пару $x$ с таким $n$, что $x_n>x_1$.

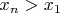
Надо по конкретнее?

-- 27.01.2026, 23:00 --

Может Вы намекаете на то что таких $x_n$ счетно, но раз их счетно, то можно выбрать наименьший, поскольку множество их номеров — подмножество натуральных чисел, а в любом подмножестве натуральных чисел есть наименьший? Но ведь не факт что наименьший по значению $x$ больший $x_1$, наименьший и по номеру среди всех икс больших $x_1$

[mihaild]

cxzbsdhwert в сообщении #1716452 писал(а):

Надо по конкретнее?

Да и так сойдет. Ну можно для очистки совести задать точно: в $x_n$ такой, что $x_n > x_1$, причем $n$ минимально (т.е. $x_k < x_1$ при $1 < k < n$).
Но это для случая $q_1 < q_2$. А для случая $q_1 > q_2$?

cxzbsdhwert в сообщении #1716452 писал(а):

Может Вы намекаете на то что таких $x_n$ счетно, но раз их счетно, то можно выбрать наименьший

Нет конечно. Как раз выбрать нельзя.

Напоминаю, что мы строим инъекцию $f: \mathbb Q \to X$. Уже определили $f(q_1) = x_1$, и почти определили $f(q_2)$ (договорите что тут нужно).
Как теперь определить $f(q_3)$? Ну и потом - пусть $f(q_1), \ldots, f(q_n)$ уже определены с сохранением порядка, как определить $f(q_{n+1})$?

[cxzbsdhwert]

mihaild в сообщении #1716456 писал(а):

Но это для случая $q_1 < q_2$. А для случая $q_1 > q_2$?

По такой же логике? $x_n$ меньший $x_1$, с наименьшим $n$ среди всех $x$ меньших $x_1$?

mihaild в сообщении #1716456 писал(а):

мы строим инъекцию $f: \mathbb Q \to X$

Если у Вас $q_n<q_{n+1}$ то мы строим инъекцию из некоторого не плотного подмножества $\mathbb Q$, или это не функция.

mihaild в сообщении #1716456 писал(а):

почти определили $f(q_2)$ (договорите что тут нужно).

$f(q_2)=x_{\min(\{n\in\mathbb N:x_n\in X>f(q_1)\})}$

mihaild в сообщении #1716456 писал(а):

Как теперь определить $f(q_3)$?

Наверное же так же

mihaild в сообщении #1716456 писал(а):

Ну и потом - пусть $f(q_1), \ldots, f(q_n)$ уже определены с сохранением порядка, как определить $f(q_{n+1})$?

Ну это так называемая полная математическая индукция, которая по одному утверждению эквивалентна существованию в любом непустом подмножестве $\mathbb N$ наименьшего. Я правда ни самой полной индукции ни доказательства утверждения не понял, как-то мутно это было объяснено, или я не придал этому значения, ну типо понимания обычной индукции мне достаточно.
$f(q_n)=x_{\min(\{n\in\mathbb N:x_n\in X>f(q_{n-1})\})}$
Ну наверное вот для такого случая нужна "полная" индукция, потому что если использовать обычную, то с учётом того что получается зависимость от предыдущего а не от следующего, то для первого было бы непонятно что.

Ну и дальше для сюръективности наверное так: поскольку $\mathbb Q$ плотно, то между $q_1$ и $q_2$ существует счетно $q$ таких что $q_1<q<q_2$, и аналогично для последующих упорядоченных пар $(q_2,q_3),...,$, $(q_n,q_{n+1})$. То есть на каждую упорядоченную пару есть счетной уникальный набор ку между ними, значит каждый из этих наборов можно занумеровать и выбрать первый из каждого. Получим снова последовательность $q_{11}<q_{12}<q_{13}<...$ (т.е. тех которые "между"). $f(q_{1n})$ тогда берём из уже заданного ранее множества для предыдущих последовательностей ку: $x_{\min(\{n\in\mathbb N:x_n\in X>f(q_{n-1})\})}$, только теперь не минимум т.е. не первые, а вторые брать.

Потом берём вторые ку и сопоставляем им третьи иксы, третьи ку и четвертые иксы ну и т.д.

[mihaild]

cxzbsdhwert в сообщении #1716493 писал(а):

Если у Вас $q_n<q_{n+1}$ то мы строим инъекцию из некоторого не плотного подмножества $\mathbb Q$, или это не функция.

У меня нет такого ограничения. Я же сказал - $q_n$ - полная нумерация всего $\mathbb Q$. В каком получится порядке.

cxzbsdhwert в сообщении #1716493 писал(а):

$f(q_n)=x_{\min(\{n\in\mathbb N:x_n\in X>f(q_{n-1})\})}$

Вы почему-то считаете, что нумерация $\mathbb Q$ монотонная. Нет, вполне может оказаться, что $q_4 < q_5 < q_3 < q_1 < q_2$, например.

cxzbsdhwert в сообщении #1716493 писал(а):

Ну наверное вот для такого случая нужна "полная" индукция

По индукции будем доказывать следующее утверждение: если существует монотонная инъекция $f: \{q_1, \ldots, q_n\} \to X$, то существует монотонная инъекция $g: \{q_1, \ldots, q_{n+1}\} \to X$, такая что $f(q_1) = g(q_1), \ldots, f(q_n) = g(q_n)$.

cxzbsdhwert в сообщении #1716493 писал(а):

Ну и дальше для сюръективности наверное так

Ничего не понятно, но подождите пока с сюръективностью.

И да, нумерация и $\mathbb Q$, и $X$ фиксирована. Менять её не понадобится.

[cxzbsdhwert]

mihaild в сообщении #1716500 писал(а):

Вы почему-то считаете, что нумерация $\mathbb Q$ монотонная

Ну сами же индексы мы возрастающе можем занумеровать, так чтобы возрастали ку? Тогда $f(q_{n_m})=x_{\min(\{n\in\mathbb N:x_n\in X>f(q_{n_{m-1}})\})}$?

mihaild в сообщении #1716500 писал(а):

По индукции будем доказывать следующее утверждение

Зачем? Это индуктивное предположение при доказательстве т.н. "шага" после доказательства "базы". Но зачем нам делать предположение о том что для произвольного $n$ инъекция существует (и из этого следует существование инъекции для $n+1$), если мы это напрямую доказали?

-- 28.01.2026, 12:41 --

пианист, написано не про возрастающую нумерацию всего $\mathbb Q$.
mihaild "как-то" занумеровал $\mathbb Q$ и предлагает рассматривать монотонную последовательность, индексы которой не обязательно монотонны, например $q_4 < q_5 < q_3 < q_1 < q_2$.
Я написал что сами индексы тогда вот так всё равно можно в порядке возрастания занумеровать же

[mihaild]

cxzbsdhwert в сообщении #1716507 писал(а):

Ну сами же индексы мы возрастающе можем занумеровать, так чтобы возрастали ку?

Не можем. Как раз потому что не существует монотонной нумерации $\mathbb Q$.

cxzbsdhwert в сообщении #1716507 писал(а):

Но зачем нам делать предположение о том что для произвольного $n$ инъекция существует (и из этого следует существование инъекции для $n+1$), если мы это напрямую доказали?

Пока не доказали. И как раз по индукции будем доказывать (и на самом деле моя формулировка имеет еще тонкий, но важный момент - существует не просто функция на первых $n+1$ элементе, но можно таким образом продолжить функцию, определенную на первых $n$ - это позволит в дальнейшем по шагам построить функцию на всех).

Вы пытаетесь сделать что-то странное и невозможное. Оно конечно потыкаться в разные стороны дело хорошее, но ИМХО Вы слишком сильно увлекаетесь. Попробуйте сделать четко по инструкции.
Определили $f(q_1) = x_1$. Теперь хотим определить $f(q_2)$ с сохранением монотонности. Рассмотрите два случая: $q_1 < q_2$ и $q_1 > q_2$.
Потом, когда определили $f(q_2)$, определите $f(q_3)$ опять же с сохранением монотонности. Какие случаи тут возможны? Что делать в каждом из них? (подсказка: $q_1$ и $q_2$ разбивают $\mathbb Q$ на три части)

[cxzbsdhwert]

mihaild в сообщении #1716522 писал(а):

Определили $f(q_1) = x_1$. Теперь хотим определить $f(q_2)$ с сохранением монотонности. Рассмотрите два случая: $q_1 < q_2$ и $q_1 > q_2$.

$f(q_{2})=x_{\min(\{n\in\mathbb N:x_n\in X>f(q_{1})\})}$ если $q_2>q_1$, или $f(q_{2})=x_{\min(\{n\in\mathbb N:x_n\in X<f(q_{1})\})}$

mihaild в сообщении #1716522 писал(а):

Потом, когда определили $f(q_2)$, определите $f(q_3)$ опять же с сохранением монотонности. Какие случаи тут возможны

Относительно чего? Ку два? Если порядок сохраняется, то есть ку три больше (меньше) ку два и ку два больше (меньше) ку один, то $f(q_{3})=x_{\min(\{n\in\mathbb N:x_n\in X>f(q_{2})\})}$ (для "меньше" аналогично).

Если порядок не сохраняется, то, если ку два больше ку один, а ку три меньше ку два, то ку три либо больше ку один либо меньше. Если больше то оно отображается в икс, который меньше того икса в который отображает ку два и больше того икса в который отображает ку один.

[mihaild]

cxzbsdhwert в сообщении #1716553 писал(а):

Относительно чего?

Что "относительно чего"? Какой порядок должен сохраняться?
И не ленитесь писать формулы, словами читать тяжело.

[cxzbsdhwert]

Я что-то запутался. Это мы что сейчас делаем? Базу полной индукции?

Для $q_4$ наверное нужно учитывать только два предыдущих (также как для $q_3$), а не всю последовательность предшествующих $q$?

Ну и дальше на шаге индукции мы показываем что если для $n>1$ первых $q$ (теперь тут уже со строго возрастающими номерами, да?) инъекция есть, то существует и для следующего (одного, то есть $n+1$ да?)

(Оффтоп)

mihaild в сообщении #1716522 писал(а):

моя формулировка имеет еще тонкий, но важный момент - существует не просто функция на первых $n+1$ элементе, но можно таким образом продолжить функцию, определенную на первых $n$

Я этого не понял. Как можно с эн плюс один "продолжить" на эн? Может наоборот?

-- 28.01.2026, 16:41 --

(Оффтоп)

mihaild в сообщении #1716563 писал(а):

И не ленитесь писать формулы, словами читать тяжело.

Мне не лень, я просто с телефона с разбитым сенсором пишу

[mihaild]

cxzbsdhwert в сообщении #1716564 писал(а):

Для $q_4$ наверное нужно учитывать только два предыдущих (также как для $q_3$), а не всю последовательность предшествующих $q$?

Всю, конечно. Нам же монотонность нужна. Вдруг $q_4 < q_1 < q_3 < q_2$, тогда надо проследить что $f(q_4) < f(q_1)$.

cxzbsdhwert в сообщении #1716564 писал(а):

Ну и дальше на шаге индукции мы показываем что если для $n>1$ первых $q$ (теперь тут уже со строго возрастающими номерами, да?) инъекция есть, то существует и для следующего (одного, то есть $n+1$ да?)

Да. Причем продолжающая инъекцию, определенную на первых $n$. Потому что в конце нам понадобится инъекции для всех $n$ соединить в одну общую.

Т.е. у нас уже определены $f(q_1), f(q_2), \ldots, f(q_n)$, причем с сохранением порядка: $q_i < q_j \iff f(q_i) < f(q_j)$ для $i, j \leq n$. Нам нужно определить $f(q_{n+1})$ тоже с сохранением порядка.

[cxzbsdhwert]

mihaild в сообщении #1716563 писал(а):

Что "относительно чего"? Какой порядок должен сохраняться?

$q_3$ должно быть больше того элемента который его меньше, и икс, соответствующий $q_3$ должен быть больше того икса, который соответствует тому элементу который меньше $q_3$.
Но элементов которых $q_3$ больше (или меньше) бесконечно и среди них могут быть $q_1$ и $q_2$. Вот я и спрашиваю — нужно обобщенно ответить, или относительно предыдущих $q$, считая что они больше или меньше?

-- 28.01.2026, 16:49 --

mihaild в сообщении #1716567 писал(а):

Всю, конечно. Нам же монотонность нужна

Так для предыдущих уже доказано. Или это логика которая должна применяться на шаге?

[mihaild]

cxzbsdhwert в сообщении #1716569 писал(а):

$q_3$ должно быть больше того элемента который его меньше

Глубокое замечание, но не очень понятно, что Вы имели в виду.

cxzbsdhwert в сообщении #1716569 писал(а):

и икс, соответствующий $q_3$ должен быть больше того икса, который соответствует тому элементу который меньше $q_3$

Это пишется так: если $q_3 > q_i$, то $f(q_3) > f(q_i)$.

cxzbsdhwert в сообщении #1716569 писал(а):

Так для предыдущих уже доказано

Я имел в виду, что при выборе значения $f(q_4)$ нам может оказаться важно значение $f(q_1)$.

Подсказываю. Мы уже определили $f(q_1), \ldots, f(q_n)$. Хотим определить $f(q_{n+1})$. Есть три варианта:
1. Для каких-то $i, j \leq n$ выполнено $q_i < q_{n+1} < q_j$.
2. Для всех $i \leq n$ выполнено $q_i < q_{n+1}$.
3. Для всех $i \leq n$ выполнено $q_i > q_{n+1}$.
Как выбрать $f(q_{n+1})$ в каждом из этих случаев?

[cxzbsdhwert]

mihaild в сообщении #1716572 писал(а):

Как выбрать $f(q_{n+1})$ в каждом из этих случаев?

Дописать $f$ и скобки вокруг $q$ которые Вы написали, а $q_{n+1}$ на искомый $x=f(q_{n+1})$ заменить:

mihaild в сообщении #1716572 писал(а):

Для каких-то $i, j \leq n$ выполнено $q_i < q_{n+1} < q_j$.

— любой $x$, такой что $f(q_i) < x<f( q_j)$
И т.д.

[cxzbsdhwert]

cxzbsdhwert в сообщении #1716576 писал(а):

— любой $x$, такой что $f(q_i) < x<f( q_j)$
И т.д.

mihaild подходит? Если да, то всё равно идей что с этим делать дальше нет. Или это сразу доказывает и сюръективность?

[mihaild]

Не бойтесь писать полные предложения, и формулы целиком.

cxzbsdhwert в сообщении #1716576 писал(а):

Дописать $f$ и скобки вокруг $q$ которые Вы написали

Что Вам мешает написать формулу вместо описания, из которого её нужно восстанавливать?

cxzbsdhwert в сообщении #1716576 писал(а):

И т.д.

А что "и т.д."?

cxzbsdhwert в сообщении #1716591 писал(а):

Или это сразу доказывает и сюръективность?

Нет конечно, таким образом легко может получиться не сюръективная функция.

Биекцию можно построить аналогичным образом, но более сложным. Давайте на $n$-м шаге, как и раньше, определим $f(q_n)$ (если она еще не определена). Но, помимо этого, определим $f(q_i) = x_n$ (если $x_n$ еще не в образе) для какого-нибудь $x_i$. Доработайте эту идею до четкого индуктивного построения - для любого $n$, если существует функция с некоторым свойством, то существует и продолжающая её функция для $n+1$ с тем же свойством.