Элементарная алгебра для отстающих

[EUgeneUS]

horda2501
Решите задачу, как умеете, без подглядывания в ответ.

[horda2501]

В этом и дело. Всё что я могу это просто подставить данные значения в формулу и получить $b(n)=\frac{2}{3} \cdot (-3)^n-1$, а откуда такие преобразования как в ответе не могу внять и близко. Далее такие же примеры с совершенно не понятными мне ответами. Я не вижу каких-то преобразований, в частности нет понимания того, откуда такие перемены в показателях степени.

[Booker48]

horda2501
Показатель степени в формуле заключайте в фигурные скобки (а всю формулу - в знаки доллара), вот так:

$a^{n-1}$

Получится $a^{n-1}$
$n-$ный член последовательности (или прогрессии) записывается вот так:

$b_n$

, это отобразится как $b_n$

[EUgeneUS]

horda2501

horda2501 в сообщении #1702645 писал(а):

и получить $b(n)=\frac{2}{3} \cdot (-3)^n-1$,

во-1х. Учимся писать степени так, чтобы они не "выпадали" сверху в строку.
Делается это так: $b(n)=\frac{2}{3} \cdot (-3)^{n-1}$

$b(n)=\frac{2}{3} \cdot (-3)^{n-1}$

т.е. с помощью фигурных скобок.

во-2х.
$b(n)=\frac{2}{3} \cdot (-3)^{n-1} = \frac{2}{3} \cdot (-1 \cdot 3)^{n-1}$

Дальше уже понятно, какими преобразованиями из Вашего ответа получить ответ из учебника?

[horda2501]

Ну этот ход мысли мне в голову приходил, мол, $-1$ взялась из-за $(-1) \cdot 3$ Но я не пойму откуда берётся $3^{n-2}$, например.

[EUgeneUS]

Хорошо, пишем дальше подробно.

$b(n)=\frac{2}{3} \cdot (-3)^{n-1} = \frac{2}{3} \cdot (-1 \cdot 3)^{n-1} = (-1)^{n-1} \cdot \frac{2}{3} \cdot 3^{n-1} = (-1)^{n-1} \cdot 2 \cdot \frac{3^{n-1}}{3}$

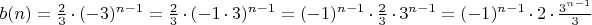
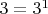
Дальше нужно вспомнить, что $3 = 3^1$ и формулу: $\frac{a^{n}}{a^m} = a^{n-m}$

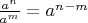
И сократить на тройку:
$b(n)= (-1)^{n-1} \cdot 2 \cdot \frac{3^{n-1}}{3} = (-1)^{n-1} \cdot 2 \cdot 3^{n-2}$

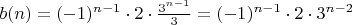Тут каждый шаг Вам нужно разобрать и понять, как он выполнялся.
Все эти преобразования являются обычными, стандартными, и должны выполняться быстро и безошибочно.

И получили в точности, как в ответе в учебнике.
-- 21.09.2025, 19:05 --

Такая запись ответа имеет свои плюсы, поэтому разберем её по частям.

1. $(-1)^{n-1}$
Этот множитель, как легко заметить, всегда по модулю равен единице (потому что $n$ - натуральное, для целых тоже справедливо). И просто меняет знак: в данном случае, для чётных $n$ - получается минус, для нечётных $n$ - получается плюс.
Это стандартная запись, когда знак выражения зависит от номера (номера в последовательности, например). И этот множитель принято писать в начале выражения, где обычно и указывается знак.

2. $2$ - некий постоянный множитель, не зависящий от номера.

3. $3^{n-2}$ - множитель, зависящий от номера.

Ваша запись (если не учитывать огрехи в записи в LaTeX) полностью эквивалентна ответу в учебнике.
Но ответ в учебнике более прозрачен и принято записывать так.

-- 21.09.2025, 19:31 --

Ещё комментарий про общепринятые варианты записей.

Например, есть выражение $-2 x \sin x$
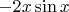
Путём перестановки множителей его можно записать кучей способов:
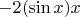
$-2 (\sin x) x$ (тут скобки обязательны, чтобы множитель $x$ "под синус" не попадал)
$2 (-1) (\sin x) x$
$(\sin x) x (-1) \cdot 2 $
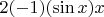
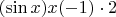
и т.д.

это будет всё тоже самое выражение, одно и то же

Но общепринятая запись (и удобная всем): $-2 x \sin x$
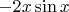
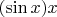
в начале знак, потом постоянный множитель, потом переменная часть. А $x \sin x$ удобнее писать, чем $(\sin x) x$, потому что скобок меньше.

Конечно, в Ваших личных промежуточных расчетах Вы можете писать эквивалентные выражения так, как Вам удобно. Но финальный ответ хорошо бы приводить к общепринятой записи.

[horda2501]

Большое спасибо! Вы всё хорошо объяснили, я всё поняла.
Вот этот момент не увидела и поэтому всё превратилось в неразрешимую задачу: $\frac{2}{3} \cdot 3^{n-1}=2 \cdot \frac{3^{n-1}}{3}$.

[horda2501]

Здравствуйте! Я добралась до учебника 10-11 Тот же коллектив авторов и, возможно, те же досадные опечатки в ответах.
Смотрите. Дана $f(x)=\frac{2x^2+3x-4}{3x+3}$ и нужно найти её значение при $f(2x^2+3x+5)$. После подстановки этого значения $x$ в числитель (в знаменателе всё сходится с ответом), я получаю с раскрытием скобок $8x^4+18x^2+25+6x^2+9x+11$. В ответе ошеломляющее меня $\frac{8x^4+24x^3+64x^2+69x+61}{6x^2+9x+18}$. Первые вопросы без ответов: откуда $x^3$ и такие большие числовые коэффициенты?

[Booker48]

horda2501 в сообщении #1703715 писал(а):

Первые вопросы без ответов: откуда $x^3$ и такие большие числовые коэффициенты?

А как Вы считали-то? Посмотрел, свободный член совпадает с тем, что и в ответе учебника.

-- 29.09.2025, 15:49 --

horda2501 в сообщении #1703715 писал(а):

откуда $x^3$

Ну, когда Вы вместо $x$ в дробь подставите $2x^2+3x+5$, то при возведении этого выражения в квадрат и появятся кубы.

[horda2501]

Видимо, я чего-то не понимаю. $(2x^2+3x+5)^2=(2)^2(x^2)^2+(3)^2x^2+5^2$ Разве не так? Я что-то делаю не так значит. Поясните кто-нибудь, что именно, пожалуйста.

[Null]

horda2501 в сообщении #1703734 писал(а):

$(2x^2+3x+5)^2=(2)^2(x^2)^2+(3)^2x^2+5^2$

$(2x^2+3x+5)^2=(2x^2+3x+5)(2x^2+3x+5)$ раскрываете скорбки.

[horda2501]

Всё, поняла с этим выражением, спасибо ( ).
Теперь не смогла понять вот это: та же функция, но $f(\frac{1}{x})$. Получается выражение: $\frac{2(\frac{1}{x})^2+3(\frac{1}{x})-4}{3(\frac{1}{x})+3}=\frac{\frac{2}{x^2}+\frac{3}{x}-4}{\frac{3}{x}+3}$. По крайней мере, такое выражение получается у меня А вот в ответе: $\frac{2+3x-4x^2}{3x+3x^2}$. Каким образом получается такое завершение?

[svv]

Умножьте числитель и знаменатель на $x^2$. Это не изменит значения дроби, но она упростится.

[wrest]

horda2501 в сообщении #1703734 писал(а):

Видимо, я чего-то не понимаю. $(2x^2+3x+5)^2=(2)^2(x^2)^2+(3)^2x^2+5^2$ Разве не так?

Пусть $x=1$ Тогда ваша левая часть $(2x^2+3x+5)^2=(2+3+5)^2=11^2=121$ а ваша правая часть $(2)^2(x^2)^2+(3)^2x^2+5^2=2^2+3^2 +5^2=4+9+25=38$
Явно что-то не так, да.
Спросите себя, почему вы не догадались такую проверку провести?

[realeugene]

horda2501 в сообщении #1703734 писал(а):

Разве не так?

Вам ещё рано изучать поля характеристики 2. Нет, с обычными числами не так.

Вы в каком классе учитесь? Вспомните бином Ньютона. Его должно быть изучают гораздо раньше. Его формулу нужно зазубрить так, чтобы помнить спросонья.