Элементарная алгебра для отстающих

[horda2501]

Хм, это настолько фундаментальная тема? Хорошо, буду прилежно разбираться в таком случае
Однако, я по прежнему решительно ничего не понимаю. Допустим, я заменила $x$ на $y$. Получилось $x=\frac{y+1}{2y-3}$. Что с этим нужно делать далее? Извините, пожалуйста, если я задаю совсем глупые вопросы. Однако, в учебнике объяснения были на простейших линейных функциях и уравнениях параболы, там ничего подобного не рассматривалось, отсюда и полнейшая беспомощность.

[Dedekind]

horda2501 в сообщении #1704835 писал(а):

Что с этим нужно делать далее?

Выразить $y$ через $x$. То есть, преобразовать выражение так, чтобы слева был $y$, а все остальное - справа. Но важнее не что делать, а зачем делать. Сначала нужно хорошо уяснить в чем суть понятия "обратная функция" и зачем она нужна (в математическом, а не практическом плане).

[horda2501]

Оба этих момента мне не ясны. Во-первых, зачем сначала переставлять переменные местами, а затем выражать одну через другую? (И как это сделать в данном случае для алгебраической дроби тоже не могу сходу вспомнить). Во-вторых, в чём суть этого понятия в нормальном объяснении понимающего для чего это будет нужно далее ума? В учебнике всё максимально банально было, мол, обратимая функция это функция, где каждому аргументу соответствует одно значение функции. Ну и что не каждая обратимая функция монотонна, а каждая монотонная обратимая. А обратную, мол, выражением $y=3x-5$ на $x=\frac{y+5}{3}$ получаете и идите далее по курсу. А в заданиях (отдельная книга к этому же учебнику) вот эти примеры с дробями, где всё в конце также через $y$.

[Dedekind]

horda2501
Функция - это машина, которой на вход мы скармливаем число, она что-то там у себя внутре с этим числом делает, и выплевывает нам на выход какое-то другое число. Так вот, представьте, что мы соединили две такие машины вход к выходу: первая принимает на вход число 2 и выплевывает число 5. Вторая принимает у нее это число 5 и выплевывает 2 (то самое, начальное). Так вот, если это повторяется для ВСЕХ возможных чисел, которые можно подавать на вход первой машины, то тогда вторая машина называется "обратная функция".

Если это понятно, то возьмите выход функции

horda2501 в сообщении #1704840 писал(а):

$y=3x-5$

(то есть, $y$) и подайте на вход функции

horda2501 в сообщении #1704840 писал(а):

$x=\frac{y+5}{3}$

. Напишите сюда результат (с ходом решения).

[miflin]

horda2501
Переобозначение Х на У связано с тем, чтобы привести выражение к стандартному виду: У - это функция, а Х - независимая переменная.
Вам ведь понятно, например, что возведение в квадрат и извлечение квадратного корня - взаимно-обратные операции.
Вот и получите $y=\sqrt{x}$ из $y=x^2$ по вышеприведенной методике.

[gefest_md]

horda2501
Если всё так плохо с обратными функциями, попробуйте представить себе функцию как множество пар чисел, где первое число - аргумент функции, второе - её значение. Ваш пример можно изобразить так.

Функция: $f=\left\{(x,y)\mid y=\frac{x+1}{2x-3}\right\}.$

Обратная функция: $f^{-1}=\left\{(y,x)\mid y=\frac{x+1}{2x-3}\right\}.$

Та же обратная функция: $f^{-1}=\left\{(y,x)\mid x=\frac{3y+1}{2y-1}\right\}.$

То же самое, но как в ответе: $f^{-1}=\left\{(x,y)\mid y=\frac{3x+1}{2x-1}\right\}.$

[miflin]

miflin в сообщении #1704855 писал(а):

Вам ведь понятно, например, что возведение в квадрат и извлечение квадратного корня - взаимно-обратные операции.

Тут, правда, возникает нюанс со знаками, но не будем о грустном.
Как подход к снаряду - годится.

[wrest]

horda2501 в сообщении #1704832 писал(а):

Если кого-либо не затруднит, скажите, а в каких случаях используется на практике нечто подобное?

Смотря что за практика. В повседневной жизни не пригодится, скорее всего.

[horda2501]

gefest_md в сообщении #1704862 писал(а):

horda2501
Если всё так плохо с обратными функциями, попробуйте представить себе функцию как множество пар чисел, где первое число - аргумент функции, второе - её значение. Ваш пример можно изобразить так.

Функция: $f=\left\{(x,y)\mid y=\frac{x+1}{2x-3}\right\}.$

Обратная функция: $f^{-1}=\left\{(y,x)\mid y=\frac{x+1}{2x-3}\right\}.$

Та же обратная функция: $f^{-1}=\left\{(y,x)\mid x=\frac{3y+1}{2y-1}\right\}.$

То же самое, но как в ответе: $f^{-1}=\left\{(x,y)\mid y=\frac{3x+1}{2x-1}\right\}.$

К сожалению, я ничего не смогла понять Каким образом всё это трансформируется? Возможно, мне нужны какие-то другие аналогии или примеры. Почему сначала просто меняются буквы местами, а потом уже и всё само выражение и каким именно образом оно меняется, по каким правилам? Я сейчас функцию воспринимаю для себя так (это предложено в определении 9 и начала 10 класса). Мол, функция определяется правилом по которому меняется значение аргумента. По какому правилу из начального $y=\frac{x+1}{2x-1}$ получается $f^{-1}=\left\{(x,y)\mid y=\frac{3x+1}{2x-1}\right\}.$
То есть, совершаются же некие алгебраические действия, так? Но какие я не могу понять.

Вот смотрите, по моей логике лица, прочитавшего объяснение к параграфу, ход решения. Я просто пытаюсь взять $x$ их числителя, мол, $5=\frac{10}{2}$, значит $x+1=y(2x-3)-1$. Ну и далее как-либо свести это к выражению через $x$ как и объяснятся на примере простейшей линейной функции $y=3x-5$ будет обратная функция $x=\frac{y+5}{3}$. Понимаете ход моего мышления? Я совершенно не осознаю откуда все эти преобразования с дробью берутся путём простой перестановки функции и аргумента местами.

[wrest]

horda2501 в сообщении #1704871 писал(а):

К сожалению, я ничего не смогла понять

Отложите, потом нагоните, в спокойном режиме.

horda2501 в сообщении #1704840 писал(а):

Во-вторых, в чём суть этого понятия в нормальном объяснении понимающего для чего это будет нужно далее ума?

Ну может вам поможет кортинко (по идее такое должно быть в вашем учебнике как иллюстрация):

зеленым цветом функция $y=\dfrac{x+1}{2x-3}$, а синим цветом -- обратная ей функция $y=\dfrac{3x+1}{2x-1}$
Красным пунктиром показана прямая $y=x$ и можно заметить (ведь можно же, да?) что синяя и зеленая кривые симметричны друг другу относительно красного пунктира (как будто взяли и поменяли местами координатные оси $x$ и $y$)

[gefest_md]

horda2501
Пример:
Зададим функцию из множества букв $\{a,b,c\}$ в множество чисел $\{1,2,3\}$ по следующему правилу: $g=\{(a,1),\ (b,2),\ (c,3)\}.$ Это правило, потому что, например, букве $a$ мы могли бы поставить в соответствие не $1,$ а $2.$ Тогда обратной для $g$ будет, по определению, функция $g^{-1}=\{(1,a),\ (2,b),\ (3,c)\}.$

Попробуйте поупражняться, находя какие пары принадлежат $f,$ и какие $f^{-1}.$ Например, $\left(0,-\frac{1}{3}\right)$ принадлежит $f.$

[horda2501]

wrest, да, совершенно верно! Есть в учебнике такое объяснение с прямой $y=x$ и симметричностью. Но оно довольно запутанное, а в чём его польза было совершенно не понятно. Теперь буду разбираться, конечно. Очень хорошо, что мне дали понять насколько эта тема важна.

[wrest]

horda2501 в сообщении #1704890 писал(а):

Очень хорошо, что мне дали понять насколько эта тема важна.

Тема как тема, обычная...
Ну само умениемвыразить одну переменную через другую бывает полезно, да.

[provincialka]

В этой теме делаются две вещи. Одна -- выразить аргумент через значение. Другая -- записать зависимость в привычном виде. Первое более важно, мне кажется.

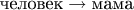
Вот давайте отойдём от математики и посмотрим на другие зависимости. Например, что означает функция "мама"? Каждому человеку ставится в соответствие его мама, $\text{человек}\to\text{мама}$. У обратной функции стрелка пойдёт в обратную сторону, $\text{мама}\to\text{человек}$.

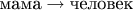
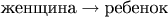
Теперь эту функцию можно записать более естественно. Мама, сама по себе -- просто женщина. А человек, который ей соотвествует -- это ее ребенок. Значит, обратным к функции "мама" будет соответствие "ребенок", $\text{женщина}\to\text{ребенок}$. Видите, мы поменяли обозначения переменных. Так же можно поменять обозначения $x$ и $y$.

У этой функции есть область определения: она применима только к женщинам, имеющим детей.

Правда, обратное соответствие уже не будет функцией, так как у одной женщины может быть несколько детей. Это как с функцией "квадрат", у которой обратное соотношение имеет, вообще говоря, два значения (корень и корень с минусом).

Другие примеры: обратным к понятию "брат" будет "сиблинг" (то есть брат или сестра). На каком множестве задано обратное соотношение? Однозначно ли оно?

Обратным к "начальник" будет "подчиненный".

А какое понятие будет обратным к понятию "муж"?

-- 08.10.2025, 06:59 --

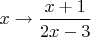
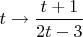
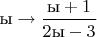
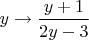
Вернемся теперь к математическому примеру. Вообще говоря, вашу функцию можно записать с помощью одной переменной, например, так: $x\to\dfrac{x+1}{2x-3}$. Или скажем, $t\to\dfrac{t+1}{2t-3}$; или $\text {ы}\to\dfrac{\text {ы}+1}{2\text {ы}-3}$ и даже $y\to\dfrac{y+1}{2y-3}$. Это всё одна и та же функция, так как важна не переменная, важна формула.

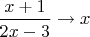
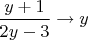
Тогда обратная функция будет иметь вид $\dfrac{x+1}{2x-3}\to x$ (ну, или $\dfrac{y+1}{2y-3}\to y$, как вам больше понравится). Вот только пользоваться такой записью неудобно. Например, зададим исходное значение $\dfrac{x+1}{2x-3}=2$.

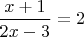
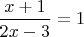
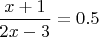
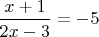
Чему будет равна праваz часть, то есть $x$? Чтобы узнать это, надо решить уравнение. И так же для других аргументов, например, $\dfrac{x+1}{2x-3}=1$, $\dfrac{x+1}{2x-3}=0.5$, $\dfrac{x+1}{2x-3}=-5$ и т.д., и т.д., и т.д....Немного утомительно, правда?

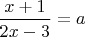
Вот поэтому лучше использовать вместо $2$, $1$, $0.5$, $-5$ какую-нибудь букву и решить уравнение в общем виде. Например, из $\dfrac{x+1}{2x-3}=a$ найти $x$ через $a$.

(второй шаг -- переобозначение переменных)