Элементарная алгебра для отстающих

[wrest]

(Даёшь бурбакизацию в школьную программу?)

ozheredov в сообщении #1712845 писал(а):

Именно: нужно сразу объяснять, что математика абстрактная наука, не имеющая ни малейшего отношения к калькуляторам, яблокам у Саши и Маши и прочим предметам из "объективной реальности" (с).

Сразу в школе? Категорически не согласен, и продолжать здесь дискуссию отказываюсь.

[Лукомор]

horda2501 в [сообщении #1712812 писал(а):

Где ошибка в понимании?

Ошибка в том, что не пройдена, либо пройдена но напрочь забыта, либо пройдена, но не понята
(нужное - подчеркнуть, ненужное - зачеркнуть) -
ТЕМА : "Порядок действий"!
Глядя на алгебраическое выражение, нужно понимать, какие действия выполняются в первую очередь, какие после них, и так далее...
Пока Вы не усвоите эту тему, будут постоянно вылезать все эти
$2+2\cdot 2 = 8$, $(2+3)^2= 13$ , $\sin x + \sin x = \sin 2x$ и прочие несуразности...

[Лукомор]

В данном конкретном случае я бы посоветовал расставлять в выражении все скобки, в том числе и те, которые опускаются обычно ввиду очевидности порядка действий.
То-есть, вместо $y = \sin x + \sin x$,
записать это выражение так:
$y = (\sin x) + (\sin x)$, что, в принципе, одно и то же самое, но дополнительные скобки хорошо сдерживают буйную фантазию, поскольку действия внутри скобок положено выполнять раньше, чем действия между скобками. Может быть это как-то поможет в понимании...

-- Сб дек 20, 2025 04:25:10 --

Аналогично, если расписать выражение $(a + b)^2$, в виде:
$(a + b) \cdot (a + b) = a \cdot (a + b) + b \cdot (a + b)$, то становится очевидным, что результат содержит не два слагаемых, а четыре, причем два слагаемых одинаковые, их можно сложить, и в итоговой формуле, получится три слагаемых, а не два.

-- Сб дек 20, 2025 04:55:18 --

horda2501 в сообщении #1712792 писал(а):

Вопрос посерьёзнее: почему же $\sin sin x + \sin x= \sin 2x$ неверное равенство, если ответ из него правильный получается?

Попробуйте самостоятельно объяснить, почему не верно равенство: $0 = \cos x - \cos x =\cos (x -x) = \cos 0 = 1$, для произвольного значения аргумента $x$.

[horda2501]

Dedekind в сообщении #1712832 писал(а):

horda2501
Это просто приоритет выполнения операций. Когда записано $x^2 + x^2$, сначала нужно возвести $x$ в квадрат, потом еще раз, и только потом сложить. А не сначала сложить, а потом возвести в квадрат. В результате получается $2x^2$, а не $(2x)^2$. С синусами $\sin x + \sin x$ то же самое: сначала вычисляется один синус, потом второй, потом результат складывается. В результате получается $2\sin x$, а не $\sin (2x)$.

Так более-менее ясно. Нужно сначала посчитать сколько действий $\sin$ будет выполняться для одинаковых $x$. Я не могу привыкнуть к этим действиям из тригонометрии, они кажутся непонятными по природе, в отличие от "простых" (вычитаний, умножений и т.д.). Нужно больше опыта Пойду решать это упражнение.

[Dedekind]

horda2501 в сообщении #1712919 писал(а):

Я не могу привыкнуть к этим действиям из тригонометрии, они кажутся непонятными по природе

Тут нужно хорошо освоить общее понятие "функция". Тогда для Вас не будет разницы, какое действие выполнять. Функция $f(x) = x^2$ ничем не лучше и не хуже функции $g(x) = \sin x$.

[Лукомор]

horda2501 в сообщении #1712919 писал(а):

не могу привыкнуть к этим действиям из тригонометрии, они кажутся непонятными по природе, в отличие от "простых" (вычитаний, умножений и т.д.). Нужно больше опыта

То-есть, Вам кажется, что к $2 + 2 \cdot 2 = 6 $ вы уже привыкли?

[sydorov]

horda2501,
чтобы не возвращаться к школьным учебникам за младшие классы, что откровенно скучно, напомню Вам упоминаемый выше порядок действий (приоритет операций)

Порядок действий. Надо запомнить - это важнее таблицы умножения

1) В первую очередь выполняются:

- возведение в степень;

- извлечение корней;

- вычисление функций (о функциях подробнее см. п. 4).

2) Во вторую очередь выполняются:

- умножение;

- деление.

3) В третью очередь выполняются:

- сложение;

- вычитание.

4) Перед вычислением функции необходимо вычислить её аргумент, если он задан выражением, по тому же порядку действий: 1)-2)-3).

Как изменить порядок действий?

С помощью скобок:
круглых $( ),$ квадратных $[ ]$ и фигурных $\{ \}.$

В этом случае вводится пункт 0) - он имеет наивысший приоритет.

0) Если в выражении есть скобки, то в первую очередь вычисляется выражение в скобках по порядку: 4)-1)-2)-3).

5) Если скобки вложены друг в друга, то сначала вычисляется выражение во внутренних скобках, затем - во внешних. Порядок действий остаётся тем же.


Для тренировки:
А. Составьте несколько простых примеров, иллюстрирующих все пункты этого правила.
Б. Из сборника конкурсных задач под редакцией М.И. Сканави решите 10 упражений из главы 1 и 20 упражнений из главы 2. Ответы для проверки присутствуют.

[Ende]

Вопросы Neznajka_ отделены в тему «О сложении синусов»

[horda2501]

Здравствуйте! Тема: "График функции $y=f(kx)$".
Я построила график $y=\sin\frac{x}{3}$ и долго радовалась тому, что теперь могу управлять этой волной Однако, построение графика $y=\sin 3x$ меня огорчило, что особенно досадно перед праздником. Дело в том, что я не могу понять как сжимать с точки зрения оси абсцисс, так как просто-напросто не хватает точек для того чтобы так сжать. Вообще не понятно как быть. Даже если использовать точку $\frac{\pi}{4}$. (Прикрепляю фото с иллюстрацией моего затруднения, очевидно, что и график $y=\sin\frac{x}{3}$ тоже неправильный из-за отсутствия $\frac{\pi}{4}$).
https://postimg.cc/68rkM8nr

[ozheredov]

horda2501
Первое, что нужно сделать - это освоить ЯЗЫК. Не для того, чтобы текстуально следовать терминологии, а чтобы отличать общепринятые понятия от не-таковых и объяснять, что, дьявол его дери, имеется в виду в каждом конкретном случае. Например:

horda2501 в сообщении #1713753 писал(а):

Я построила график $y=\sin\frac{x}{3}$ и долго радовалась тому, что теперь могу управлять этой волной

Как можно УПРАВЛЯТЬ непараметризованной хвункцией? Надо было написать: управлять = подставлять вместо 3 произвольное число и радоваться тому, как гармошка сжимается/распрямляется. Далее:

horda2501 в сообщении #1713753 писал(а):

Дело в том, что я не могу понять как сжимать с точки зрения оси абсцисс

Я всё понял, но оборот "с точки зрения оси абсцисс" способен так резануть по глазам, что из Вашей темы убегут. А вот тут уже катастрофический <пневмослон>:

horda2501 в сообщении #1713753 писал(а):

так как просто-напросто не хватает точек для того чтобы так сжать

Здесь можно только вставить видео известного мема из рекламы "Курсы иностранных языков в Балашихе": Чего, @#^&+??? Теперь по теме: представьте, что график любой вменяемой функции $g(x)$ состоит из таких забавных цветных кружочков, являющихся решениями уравнения $g(x)=c$ для всевозможных $c$. Допустим, решения уравнения $f(x)=c$ известны. Как ведут себя решения $f(kx)=c$?

[horda2501]

Я думаю, что вполне понятно, что у меня сейчас уровень освоения темы "2+3" То есть, всё очень просто, что можно увидеть на картинке. Поясню. Например, я растягиваю график с коэффициентом растяжения $3$. Это значит, что второе (после начала координат) "касание" волны оттаскивается с $\pi$ до $\3pi$. Таким образом, все остальные точки тоже на 3 шага съезжают вправо. Эти шаги - деления на оси абсцисс. Ранее я пользовалась (по примерам из учебника, упрощённым максимально) делениями по 30 градусов. То есть, отсутствовало между 0 и $\frac{\pi}{2}$ деление $\frac{\pi}{4}$. Это можно видеть на картинке, там цена деления это одна клетка. С этой точки зрения мой график вроде как правильный. Однако, в следующем упражнении на сжатие с коэффициентом $3$ это уже не работает. Я "подключила" деление $\frac{\pi}{4}$ между этими клетками, ну и всё. Очевидно, что это не работает, так как некуда сжать всё равно с таким ходом мысли. Более того, что будет если коэффициент будет ещё больше, например, $5$? Здесь у меня не хватает какого-то общего понимания, как работать с этими делениями на оси абсцисс, наверное. Вообщем нужна помощь.

[wrest]

horda2501 в сообщении #1713753 писал(а):

Дело в том, что я не могу понять как сжимать с точки зрения оси абсцисс, так как просто-напросто не хватает точек для того чтобы так сжать.

Дарю вам точек побольше (откроется по клику)

Вертикальные линии потолще проведены через $0,1 \pi$ а линии потоньше через $0,02 \pi$
Если захотите ещё сильнее сжимать, дайте знать - пришлю вам точек ещё почаще.

[ozheredov]

horda2501

График существует только в тех точках $x$, в которых заданы деления, или между делениями тоже какая-то движуха происходит?

[wrest]

horda2501 в сообщении #1713759 писал(а):

Более того, что будет если коэффициент будет ещё больше, например, $5$?

При таком большом коэффициенте уже может понадобиться зрительная лупа, а дальше, возможно, и микроскоп.
Для таких вот подробных работ делают специальную бумагу, называется "миллиметровка".

Например на озоне можно купить 5 метров длиной и 87см высотой рулон за 200 руб., см. тут:
Бумага миллиметровая масштабно-координатная для выкроек и черчения, рулон 88 см*5 м, Айрис
https://ozon.ru/t/mzYlwGE

[horda2501]

ozheredov в сообщении #1713762 писал(а):

horda2501

График существует только в тех точках $x$, в которых заданы деления, или между делениями тоже какая-то движуха происходит?

Подобные вопросы на данный момент не затрагивались в тексте учебника. Там даны лишь "удобные" для объяснения абсолютным новичкам, вроде меня, примеры, которые не позволяют об этом задуматься без заданий из другой части учебника (упражнения). К сожалению, я не могу сама понять как это работает.

Изначально за основу дана числовая окружность, на ней в каждой четверти три деления с $\pi$ (30, 45, 60 градусов). Далее всё это из каждой четверти переносится на ось абсцисс в числовой системе координат. Потом предлагается на этих делениях сжимать или растягивать волну в зависимости от коэффициента. Но теперь из этого ничего не выходит, так как не хватает этих делений, а коэффициент может быть сколько угодно большой. Я понятно изложила что вызывает у меня затруднения?

Вопрос: исходя из чего нужно назначать эти деления и как они связаны с коэффициентом? Как всегда проще на конкретном примере. Вот мне нужно сжать синус с коэффициентом $3$. Как я должна работать? Пошаговые мысли, алгоритм, то есть. В примере в учебнике была функция $y=\cos 2x$ и там волна просто сжималась от плюс-минус $\frac{\pi}{2}$ до $\frac{\pi}{4}$ в зависимости от конца. То есть, делался "шаг" по числовой прямой (если справа на налево) $\frac{\pi}{2}-\frac{\pi}{3}-\frac{\pi}{4}-\frac{\pi}{6}-0$. 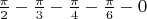Числовой коэффициент $2$ значит два шага и ты попадаешь в $\frac{\pi}{4}$. Остальные точки смещаются симметрично. Что делать в случае, если коэффициент функции превышает число этих делений? То есть, как на графике в моей картинке. Я смещаю на три шага до $\frac{\pi}{3}$, если слева направо от 0. Этому будет соответствовать на оси ординат $\frac{1}{2}$. А для деления $\frac{\sqrt{3}}{2}$ уже ничего и не остаётся. Если коэффициент сжатия $5$ и более это уже и не волна, а фонтан. Вобщем, не ясно каким образом можно решать такие задачи на данном этапе. Если вводить какие-то новые деления, то не ясно как именно и как они на двух осях будут коррелировать.