Практика не может быть критерием истины напрямую в абстрактных науках, только косвенно через применение знаний из абстрактных наук в эмпирических науках и прикладной деятельности.
С этим я не спорю.
И уж конечно у большинства наук нет никакой общечеловеческой пользы и это совсем не только философии касается: демографы занимаются демографией и population studies не ради какой-то общечеловеческой пользы, а практическая польза демографии существенно ограничена - например, стимулирующая (пронаталистская) и дестимулирующая (антинаталистская) политика в области рождаемости по сути не работает на уровне реальных поколений.
Сложно сформулировать термин "общечеловеческая польза", я про него не говорил. Речь идет об общечеловеческой потребности в практической пользе, а практическая польза может пониматься по-разному. И если говорить про практическую пользу демографии, то не думаю,что с вашим личным мнением ее почти полного отсутствия согласится значимое сообщество демографов.
И в этом вопросе я не стал бы отделять науку от общества. Наука - это все-таки общественное явление. Если определенный социум, нерелевантный с вашими исследованиями, платит деньги за исследования или использует какую-либо другую систему стимуляции, то предполагается, что, как минимум, практическую пользу вы приносили ранее или принесете в будущем. Критерием разделения здесь опять же является практика - если продолжительное время никакой предполагаемой пользы не удается получить, то и исследования сворачиваются.
Что касается философии, то верифицировать ее пользу через транформацию идей в что-то практическое почти невозможно. Там всегда неформальные рассуждения, которые часто сложно отличить от языковых галлюцинаций ИИ. Да, в неизвестной области такие неформальные абстрактные рассуждения иногда помогают нащупать что-то интересное, и когда они приобретают форму (если таковое случается), то становятся наукой (точным знанием). Но в истоках своих - это преднаука.
-- Чт сен 11, 2025 18:45:45 --Точки зрения «мирской науки» и «науки священной» несовместимы и даже противоречат друг другу.
Г. Харди тоже так думал: "Я никогда не делал чего-нибудь «полезного». Ни одно моё открытие не принесло и не могло бы принести, явно или неявно, к добру или ко злу, ни малейшего изменения в благоустройстве этого мира."
-- Чт сен 11, 2025 18:56:21 --Нет, не об этом. Натуральные числа можно очень по-разному определять. В лямбда исчислении 3 можно определить как
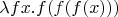
. Это один из способов введения натуральных чисел ("нумералы Черча"). Причем даже в рамках этого способа то же умножение можно ввести разными способами, например, как
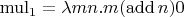
, где
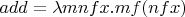
. Или
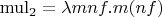
. То есть у нас уже 2 разных определения натуральных чисел и, соответственно, два разных числа 3. Кроме нумералов Черча есть еще способы. Это я пока про бестиповое лямбда исчисление говорил. А этих лямбда исчислений выше крыши. Даже если определить натуральные числа точно так же (как нумералы Черча), но в каком-нибудь из типизированных лямбда исчислений (например, в просто типизированном) - это уже будут другие натуральные числа и другое число 3. Есть куча формальных систем, созданных под натуральные числа: PA1, PA2, Пресбургера, Робинсона и тд. В каждой из них число 3 - это разные объекты. Далее, можно рассмотреть несколько теорий множеств: ZF, ZFC, MK, TG, NBG и определить в них натуральные числа - и это все будут разные натуральные числа. Да даже в рамках одно теории множеств, например, ZFC, можно ввести натуральные числа несколькими способами: минимальное индуктивное множество, конечные ординалы, конечные кардиналы. Тоже все разные натуральные числа. И еще. Вы же сказали просто "число 3", а не "натуральное число 3". Тогда еще подойдет куча смыслов, связанных с тем, что под "3" можно понимать и целое, и рациональное, и действительное, и комплексное, и Леви-Чивита, и кучу еще разных троек. В общем, в классе "число 3" сильно больше, чем 10 представителей (формально - вообще бесконечно много, т.к. даже в одном только бестиповом лямбда исчислении можно напридумывать кучу формально различных определений натуральных чисел, навешивая на нумералы Черча какие-нибудь бесполезные самосокращающиеся метки).
Не вижу никакого противоречия. Есть сущность со вполне определенными свойствами, которую в разных теория можно по-разному назвать, обозначить.