Zeros po |sz| Sum|sz| sred
1 10000 139195 900276363 90028
10 10000 171368 1331232484 133123
10^2 10000 183015 1604809531 160481
10^3 10000 166673 1700134166 170013
10^4 10000 194864 1721360182 172136
10^5 10000 197800 1724177191 172418
10^6 10000 195003 1724961362 172496
1 70000 16765 6301573748 90022
10 70000 57569 9320493824 133150
10^2 70000 1695 11247383712 160677
10^3 70000 118036 11885628527 169795
10^4 70000 124984 12043964310 172057
10^5 70000 143606 12073168359 172474
10^6 70000 146850 12078135936 172545
1 100000 122815 9002293421 90023
10 100000 161541 13315241559 133152
10^2 100000 334696 16068596690 160686
10^3 100000 301317 16983028632 169830
10^4 100000 327975 17205014312 172050
10^5 100000 315867 17245888382 172459
1 125000 136494 11252862408 90023
10 125000 268568 16647124366 133177
10^2 125000 146573 20073991102 160592
10^3 125000 154253 21228909304 169831
10^4 125000 228757 21502748259 172022
10^5 125000 240968 21556755412 172454
1 250000 75603 22505673238 90023
10 250000 226428 33292989782 133172
10^2 250000 189964 40150003553 160600
10^3 250000 325828 42407717991 169631
10^4 250000 257542 42948901721 171796
1 400000 115936 36009052749 90023
10 400000 228743 53257052847 133143
10^2 400000 230202 64213154241 160533
10^3 400000 220369 67868537694 169671
10^4 400000 204832 68739019920 171848
1 500000 129842 45011347142 90023
10 500000 173535 66572561594 133145
10^2 500000 83187 80252871814 160506
10^3 500000 25828 84815012483 169630
1 1000000 99362 90022571971 90023
10 1000000 178442 133152447455 133152
10^2 1000000 373457 160511604562 160512
10^3 1000000 447390 169659558631 169660





 являются слабо зависимыми случайными величинами и их среднее, на основании Закона больших чисел, стремится к мат. ожиданию при неограниченном увеличении числа нулей.
являются слабо зависимыми случайными величинами и их среднее, на основании Закона больших чисел, стремится к мат. ожиданию при неограниченном увеличении числа нулей. понятно какая, но знак-то непонятен.
понятно какая, но знак-то непонятен. ? Номер нуля? Кстати, на всякий случай проверил разные знаки. Множитель при
? Номер нуля? Кстати, на всякий случай проверил разные знаки. Множитель при  :
: слева, увеличивая
слева, увеличивая  скажем с шагом
скажем с шагом  , каждый раз перевычисляя первую строку, то есть
, каждый раз перевычисляя первую строку, то есть  с точностью до тысячных. Сначала
с точностью до тысячных. Сначала  , затем примерно в точке
, затем примерно в точке  начинает раскачиваться, методично оказываясь по обе стороны от нуля, со всё возрастающей амплитудой.
начинает раскачиваться, методично оказываясь по обе стороны от нуля, со всё возрастающей амплитудой. . В точке
. В точке  значение как раз
значение как раз  , но теперь уже оно не возвращается к
, но теперь уже оно не возвращается к  происходит устаканивание — значение
происходит устаканивание — значение  .
. сумма по дзета-нулям вновь почувствует простое число и начнёт колебаться, методично оказываясь по обе стороны теперь уже от единички, со всё возрастающей амплитудой. Длина волны при этом при этом снова постоянная, но уже гораздо больше — примерно
сумма по дзета-нулям вновь почувствует простое число и начнёт колебаться, методично оказываясь по обе стороны теперь уже от единички, со всё возрастающей амплитудой. Длина волны при этом при этом снова постоянная, но уже гораздо больше — примерно  .
. значение как раз
значение как раз  , но теперь уже оно не возвращается к
, но теперь уже оно не возвращается к  происходит устаканивание — значение
происходит устаканивание — значение  .
. . 6-ка не является простой степенью, поэтому
. 6-ка не является простой степенью, поэтому  почти на всём пути от 5 до 7, начиная колебаться только вблизи этих чисел.
почти на всём пути от 5 до 7, начиная колебаться только вблизи этих чисел. . То есть брал ровно миллион первых нулей.
. То есть брал ровно миллион первых нулей. ,
,  и
и  — для них
— для них  — не ловится.
— не ловится. используя
используя  предвычисленных нулей дзета-функции Римана.
предвычисленных нулей дзета-функции Римана. имея предвычисленный массив из
имея предвычисленный массив из  нетривиальных нулей дзета-функции и сейчас все крутится вокруг
нетривиальных нулей дзета-функции и сейчас все крутится вокруг  : вот Платт точно посчитал
: вот Платт точно посчитал  имея
имея  нулей дзета-функции (
нулей дзета-функции (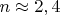 ),
),