Точное количество кортежей из простых чисел в интервале

[vicvolf]

Yadryara в сообщении #1688792 писал(а):

vicvolf в сообщении #1688787 писал(а):

А зачем Вы инфу из постов дублируете??

Бывает, лапухнулся

[Yadryara]

Yadryara в сообщении #1688758 писал(а):

Планирую продолжать: исследовать сумму теперь уже по трём первым нулям.

Да, это как задача трёх тел. С двумя нулями закономерность видна и подтверждается, я её ещё дальше проверил, а с 3 нулями уже ничего понять невозможно. Ну или надо очень долго исследовать.

Вот 41 точка в интервале 1e1 — 1e4:

Используется синтаксис Text

Для этих x сумма по 3 первым дзета-нулям обращается в ноль.

                 x   posl/pred
1           11.579 
2           14.859     1.283
3           17.688     1.190
4           20.833     1.178
5           23.688     1.137
6           25.420     1.073    *
7           29.527     1.162
8           34.934     1.183
9           42.312     1.211
10          53.950     1.275
11          66.135     1.226
12          70.233     1.062    *
13          72.441     1.031    *
14          88.326     1.219
15         104.423     1.182
16         123.017     1.178
17         140.514     1.142
18         148.196     1.055    *
19         173.337     1.170
20         206.972     1.194
21         258.810     1.250
22         314.973     1.217
23         373.599     1.186
24         406.377     1.088    *
25         443.615     1.092    *
26         522.848     1.179
27         617.113     1.180
28         731.445     1.185
29        1009.874     1.381
30        1236.213     1.224
31        1553.130     1.256
32        1851.367     1.192
33        2174.967     1.175
34        2392.590     1.100    *
35        2633.170     1.101    *
36        3087.830     1.173
37        3652.841     1.183  
38        4425.961     1.212
39        5801.336     1.311
40        7616.924     1.313
41        9225.637     1.211
 

Можно и дальше посчитать эти точки, например до 1e30, они конечно могут пригодиться, так как для них оценка $\pi(x)$ ещё точнее.

Ещё есть смутная идея вероятностные методы попробовать.

[wrest]

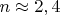Я правильно понимаю, что примерная цель в этой теме -- определить можно ли вычислить $\pi(x)$ имея предвычисленный массив из $x^{1/n}$ нетривиальных нулей дзета-функции и сейчас все крутится вокруг $n=2$: вот Платт точно посчитал $\pi(10^{24})$ имея $7\cdot 10^{10}$ нулей дзета-функции ($n\approx 2,4$), но хотелось бы $n$ увеличить, хотя бы до 3 и если крупно повзёт (т.е. вы сделаете большое открытие), то до 6.
При этом, как я понимаю, у вас там речь об $x \approx 10^{24}$

[vicvolf]

Yadryara в сообщении #1688702 писал(а):

Ну то бишь считали максимум по 176-й ноль, который равен 359.7437549531144487992919859769902 ?

Да, вот подробнее:
J(500.0) ≈ 101.3814519367412386560931
Использовано пар нулей: 176 (всего нулей: 352)
Последний учтенный ноль: ρ = 0.5 + 359.743754953114448799292i
Мнимая часть последнего нуля: |γ| = 359.743754953114448799292

Дополнительно:
Li(x) = 101.7938724886266594879964
Сумма по нулям = 0.2807266286745244775138909
Поправочный интеграл ≈ 0 (пренебрежимо мал)

Точность уменьшил до 25 знаков.

[Yadryara]

wrest, нет неправильно. Ведь в заголовке темы есть слово "кортежей".

Задача-максимум, которая выглядит нереально — найти точную формулу хотя бы для какого-нибудь простейшего кортежа. А для этого нужно понимать как, например, считал Платт сотоварищи. Вы понимаете?

Более реалистичная вроде бы задача: отыскание способа, который бы оценивал количество кортежей в интервале лучше чем HL1, а это пока наилучший известный способ.

Пример из практики. Для первого интервала матожидание знаменитого кортежа было 0.51 штуки, а для второго интервала — 0.33 штуки. Но он нашёлся во втором интервале, а не в первом.

Почему? Таковы флуктуации. А кто за них отвечает? Те самые нули дзета-функции. Правильно понимаю?

[Dmitriy40]

Yadryara в сообщении #1688857 писал(а):

найти точную формулу хотя бы для какого-нибудь простейшего кортежа. А для этого нужно понимать как, например, считал Платт сотоварищи.

Почему Вы думаете что второе связано и чем-то поможет с первым?
При том что первое по значимости ИМХО сравнимо с ВТФ.

[Yadryara]

Dmitriy40 в сообщении #1688887 писал(а):

Почему Вы думаете что второе связано и чем-то поможет с первым?

До тех пор пока не пойму как посчитано у Платта, воздержусь от ответа.

Dmitriy40 в сообщении #1688887 писал(а):

При том что первое по значимости ИМХО сравнимо с ВТФ.

Странно. Вы сами говорили, что ни разу не математик. И как Вы можете себе представлять обе эти значимости

[vicvolf]

Yadryara в сообщении #1688912 писал(а):

До тех пор пока не пойму как посчитано у Платта, воздержусь от ответа.

Давайте вернемся в тему topic160103-15.html

[Yadryara]

vicvolf, кто ж против-то. И Вы наконец-то нормальным русским языком объясните как у Платта посчитано? Именно как посчитано, а не как обосновано? Не будете отсылать книжки читать?

Вы видели как мы терпеливо объясняли Evgeniy101 на численных примерах? Я и с одной и с другой стороны заходил, пытался понять где же он теряет нить. А он её терял даже тогда когда уже вроде бы научился считать разрешённые остатки. Предположил, что он не понимает что в периоде должны встретиться именно все возможные комбинации этих самых разрешённых остатков. Объяснил, расписал подробно на простейшем примере. И только тогда, наконец, произошёл прорыв.

Заметьте, мы его не отправляли книжки читать, потому что это было необязательно. Я подозреваю, что и в случае с Платтом необязательно. Хотите начать издалека, извольте, я внимательно слушаю. Даже если Вам так уж хочется знать моё мнение почему кортеж 3, 5, 7 единственный, отвечу.

Хотя я бы предпочел остаться здесь, стоит ли по темам скакать.

[vicvolf]

Yadryara в сообщении #1688946 писал(а):

vicvolf, кто ж против-то. И Вы наконец-то нормальным русским языком объясните как у Платта посчитано? Именно как посчитано, а не как обосновано? Не будете отсылать книжки читать?

Ну уж как умею. Вы же про одержимость читали. Теперь пытаетесь Платта понять. Надо уровень постепенно поднимать!

Вот какие вычислительные ресурсы использовал Платт:

Система: Кластер Bluecrystal Phase II (Университет Бристоля).

Время: 63 000 CPU-часов (~7.2 года на одном ядре).

Параллелизация: Распределение вычислений суммы по нулям и просеивания.

[Yadryara]

vicvolf в сообщении #1688964 писал(а):

Ну уж как умею.

Тут не в умении дело, а в открытости.

Вот же я спросил:

Yadryara в сообщении #1688285 писал(а):

Вот они взяли полосу $ 10^{24}\pm 6\cdot10^{15}$ Что они дальше делали?

Почему не ответили по существу? Что трудно сказать прямо: "я не знаю" или "я не понимаю"?

[vicvolf]

https://www.cambridge.org/core/services ... ervals.pdf

vicvolf в сообщении #1689604 писал(а):

При условии справедливости HL1 расстояние между простыми кортежами имеет экспоненциальное распределение с параметром $C/\ln^k(N)$
https://ru.wikipedia.org/wiki/%D0%AD%D0 ... 0%B8%D0%B5
Теорема Галлахера (1976):
При условии гипотезы Харди-Литтлвуда, количества простых в непересекающихся интервалах асимптотически независимы и распределены по Пуассону. Это влечёт экспоненциальность расстояний.

[vicvolf]

Yadryara Помню Вы писали, что Вас не устроила точность предсказания появления кортежа, что реальное значение было значительно меньше среднего значения подсчитанного по HL1.
На основании сказанного выше расстояния между простыми кортежами имеют экспоненциальное распределение. Данное распределение справа от среднего имеет длинный хвост, а слева - обрезано. Поэтому вероятность, что расстояние между простыми кортежами не превосходит среднее больше вероятности, чем не превосходит.
Вот доказательство этого факта.

Пусть $X$ — случайная величина с экспоненциальным распределением с параметром $\lambda > 0$. Тогда:

Среднее значение (математическое ожидание):

$\mathrm{E}[X] = \frac{1}{\lambda}$

Функция распределения:

$F(x) = P(X \leq x) = 1 - e^{-\lambda x}, \quad x \ge 0$

Найдем вероятность того, что $X$ не превосходит своё среднее, то есть

$P\left(X \leq \mathrm{E}[X]\right) = P\left(X \leq \frac{1}{\lambda}\right)$

Подставим в формулу:

$P\left(X \leq \frac{1}{\lambda}\right) = 1 - e^{-\lambda \cdot \frac{1}{\lambda}} = 1 - e^{-1} \approx 1 - 0.3679 = 0.6321$

То есть вероятность, что случайная величина с экспоненциальным распределением не превысит своё среднее значение, примерно равна 63.2%.

Это объясняет, что реальное значение было меньше среднего значения подсчитанного по HL1.

[Yadryara]

vicvolf в сообщении #1689953 писал(а):

Yadryara Помню Вы писали, что Вас не устроила точность предсказания появления кортежа, что реальное значение было значительно меньше среднего значения подсчитанного по HL1.

Неплохо бы цитату. Вот я совсем недавно сравнивал предсказания по HL1 с фактами:

Yadryara в сообщении #1685688 писал(а):

А вот и сравнение с Базами:

№     Паттерн    Прогноз   Факт
1.   13-168          262    252
2.   13-180-1        279    282
3.   13-180-2        415    447
4.   13-180-3        727    696
5.   13-180-4        568    544
6.   13-180-5        185    195
7.   13-180-6        594    622
8.   13-180-7        686    737
9.   13-180-8        533    519
10.  13-180-9        693    673
11.  13-180-10       503    523
12.  13-192-1        226    232
13.  13-192-2        195    214
14.  13-192-3        124    103    17 %
15.  13-192-4        158    145
16.  13-192-5        246    250
17.  13-192-6        276    285
18.  13-204-1        126    132
19.  13-204-2        173    171
20.  13-204-3        283    282
21.  13-204-4        208    180
_______________________________
                    7462   7484   0.3 %

HL1 по-прежнему прекрасно предсказывает. Вот бы ещё понять как учесть нули дзета-функции Римана, чтобы предсказывать ещё точнее...

vicvolf в сообщении #1689953 писал(а):

Поэтому вероятность, что расстояние между простыми кортежами не превосходит среднее больше вероятности, чем не превосходит.

У Вас оба раза написано: не превосходит.

vicvolf в сообщении #1689953 писал(а):

$P\left(X \leq \frac{1}{\lambda}\right) = 1 - e^{-\lambda \cdot \frac{1}{\lambda}} = 1 - e^{-1} \approx 1 - 0.3679 = 0.6321$

Спасибо, хотя эту формулу я знал.

[vicvolf]

Yadryara в сообщении #1689963 писал(а):

Неплохо бы цитату. Вот я совсем недавно сравнивал предсказания по HL1 с фактами:.....

Я имел в виду другую:

Yadryara в сообщении #1688857 писал(а):

Пример из практики. Для первого интервала матожидание знаменитого кортежа было 0.51 штуки, а для второго интервала — 0.33 штуки. Но он нашёлся во втором интервале, а не в первом. Почему? Таковы флуктуации. А кто за них отвечает?

Я объяснил почему 0,51 и 0,33, т.е. меньше мат. ожидания выше в теме.