Точное количество кортежей из простых чисел в интервале

[Yadryara]

Yadryara в сообщении #1691826 писал(а):

Что мешает считать простое число кортежем длиной 1 и диаметром 0?

Здесь я имел в виду что эту тему можно считать более общей, включающей ту тему в качестве частного случая.

vicvolf в сообщении #1691842 писал(а):

При совместном предположении Х-Л и расширенной гипотезы Римана действительно существует возможность получить оценки для количества простых кортежей с явным остаточным членом, выраженным через сумму по нулям дзета-функции Римана. Это является нетривиальным обобщением классической формулы Римана для простых чисел.

Обрадовали. Разумеется для практических целей обе гипотезы надо полагать верными, поскольку не известно ни одного контрпримера.

[Yadryara]

Запишу в привычной упрощённой форме для кристаллов длиной до 3-х:

$$\pi(x)\approx\operatorname{C0}_1\int\limits_{2}^{x}\frac{dt}{\ln{t}}$$

$$\pi_2(x)\approx\operatorname{C0}_2\int\limits_{2}^{x}\frac{dt}{\ln^2{t}}$$

$$\pi_3(x)\approx\operatorname{C0}_3\int\limits_{2}^{x}\frac{dt}{\ln^3{t}}$$

Чтобы равенство стало точным добавлю так называемый остаточный член:

$$\pi(x)=\operatorname{C0}_1\int\limits_{2}^{x}\frac{dt}{\ln{t}}+Z_1$$

$$\pi_2(x)=\operatorname{C0}_2\int\limits_{2}^{x}\frac{dt}{\ln^2{t}}+Z_2$$

Для кортежей длиной $1$ $\operatorname{C0}_1=1$ и остаточный член состоит из множества слагаемых, самым важным из которых является сумма по дзета-нулям $sz$:

$$\pi(x)=\int\limits_{2}^{x}\frac{dt}{\ln{t}}+sz+z$$

Вот я и предлагаю пока понять как оценивать величину $sz$.

[vicvolf]

Yadryara в сообщении #1691949 писал(а):

$$\pi(x)=\int\limits_{2}^{x}\frac{dt}{\ln{t}}+sz+z$$

Вот я и предлагаю пока понять как оценивать величину $sz$.

Если гипотеза Римана верна, то для всех x⩾ 2657 выполняется $|\pi(x)-\int_2^x \frac {dt}{\ln(t)}| < \frac {x^{1/2}\ln(x)}{8\pi}$.

[Yadryara]

Да, это есть здесь: Prime-counting_function.

То бишь

$$|sz + z| < \frac {\sqrt{x}\ln{x}}{8\pi}$$

Вспоминаем что $sz ={\sum\limits_{i=1}^{\infty} \operatorname{li}(x^{\rho_i})$

Тогда можно ли записать, что

$$|sz| < \frac {\sqrt{x}}{\ln{x}}$$

для всех $2\leqslant{x}<10^{316}$ ?

[vicvolf]

Yadryara в сообщении #1691989 писал(а):

для всех $2\leqslant{x}<10^{316}$ ?

Там же модуль, поэтому сверху нет ограничений. Формулу, которую я привел дается с учетом все нетривиальный нулей. Если известно ограниченное количество нулей, то оценка ухудшается.

[Yadryara]

vicvolf в сообщении #1692011 писал(а):

Там же модуль, поэтому сверху нет ограничений.

Опять на разных языках говорим? Вблизи $1.4\cdot10^{316}$ (первое?) Литлвудово нарушение, там предположительно

$$|sz|>1.019\frac{\sqrt{x}}{\ln{x}}$$

[vicvolf]

Yadryara в сообщении #1692021 писал(а):

Вблизи $1.4\cdot10^{316}$ (первое?) Литлвудово нарушение, там предположительно

$$|sz|>1.019\frac{\sqrt{x}}{\ln{x}}$$

Литлвудово нарушение - это когда $\pi(x) \geq Li(x)$, т.е. меняется знак остатка, но на модуль остатка это не влияет.

[Yadryara]

Точно на разных языках разговариваем. Вроде всё просто и обозначения говорящие. Остаточный член разделил на две части: $sz$ (Sum of Zeroes) плюс $z$

Чтобы Литлвудово нарушение здесь произошло нужно чтобы $sz$ была очень большой и положительной.

Как раз такой очень большой она в этой области и является, потому что среднее значение по последним данным

$$|sz|\approx0.1726\frac{\sqrt{x}}{\ln{x}}<< 1.019\frac{\sqrt{x}}{\ln{x}}$$

Нули здесь входят в резонанс.

[vicvolf]

Yadryara в сообщении #1692067 писал(а):

Остаточный член разделил на две части: $sz$ (Sum of Zeroes) плюс $z$

А что такое z?

[Yadryara]

Надеялся что это очевидно: все остальные слагаемые. Я конечно опять могу отослать к 409-й бумажной странице Дербишира, но чувствую лучше будет не полениться и таблицу нарисовать.

[Yadryara]

Давайте посчитаем по точной формуле Римана, сколько имеется простых чисел не превышающих 100:

$\tikz[scale=.09]{ \fill[green!30!blue!20] ( 0,50) rectangle ( 20,60); \fill[green!30!grey!40] (20,50) rectangle ( 40,60); \fill[green!90!blue!50] (80, 0) rectangle (100,10); \draw[step=20cm] (0,0) grid +(100,60); \draw (0,10) -- (100,10); \draw (0,30) -- (100,30); \draw (0,50) -- (100,50); \node at (10,55){\text{30.126}}; \node at (10,45){\text{-3.083}}; \node at (10,35){\text{-1.136}}; \node at (10,25){\text{-0.336}}; \node at (10,15){\text{0.209}}; \node at (30,55){\text{-0.900}}; \node at (30,45){\text{0.070}}; \node at (30,35){\text{0.075}}; \node at (30,25){\text{0.011}}; \node at (30,15){\text{0.055}}; \node at (50,55){\text{-0.693}}; \node at (50,45){\text{0.347}}; \node at (50,35){\text{0.231}}; \node at (50,25){\text{0.139}}; \node at (50,15){\text{-0.116}}; \node at (70,55){\text{0.000}}; \node at (70,45){\text{-0.001}}; \node at (70,35){\text{-0.004}}; \node at (70,25){\text{-0.013}}; \node at (70,15){\text{0.018}}; \node at (90,55){\textbf{28.533}}; \node at (90,45){\textbf{-2.667}}; \node at (90,35){\textbf{-0.834}}; \node at (90,25){\textbf{-0.199}}; \node at (90,15){\textbf{0.166}}; \node at (10,5){\textbf{25.780}}; \node at (30,5){\textbf{-0.689}}; \node at (50,5){\textbf{-0.092}}; \node at (70,5){\textbf{0.000}}; \node at (90,5){\textbf{24.999}}; }$

Интегральный логарифм от 100 у нас в левом верхнем углу, а $sz$ (сумма по дзета-нулям) от 100 чуть правее. Они выделены цветом, как и итоговый результат. Суммы по строкам и столбцам выделены болдом.

Батороев, vicvolf, wrest, gris, ... спрашивайте, если непонятно как посчитано хотя бы одно число в этой таблице.

Дмитрию, надеюсь, понятно всё. Ибо книгу довольно внимательно читал.

vicvolf в сообщении #1692118 писал(а):

А что такое z?

$z$ это сумма всех остальных 18 чисел обычным шрифтом в таблице.

Правда, надо ещё учесть отличие в 1.045 между интегральным логарифмом и сдвинутым им же.

[vicvolf]

С расчетом понятно, а теперь немного аналитики.

Стандартная формула (см. Davenport, "Multiplicative Number Theory", Ch. 17; Ingham, "The Distribution of Prime Numbers", Ch. IV) выглядит так:

$\pi(x) = \operatorname{li}(x) - \sum_{\rho} \operatorname{li}(x^{\rho}) - \log 2 + \int_{x}^{\infty} \frac{dt}{t(t^2-1) \log t} + \text{малые вклады от простых степеней}.$

Разберем каждый компонент:

1. $ \log 2 \approx 0.693147. $

2. Интегральный член: $\int_{x}^{\infty} \frac{dt}{t(t^2-1) \log t}$
Асимптотическая оценка:
$ \int_{x}^{\infty} \frac{dt}{t(t^2-1) \log t} = O\left( \frac{1}{x \log x} \right). $

3. Вклады от простых степеней (prime powers)
- Если $\pi(x)$ считает только простые числа (без степеней), то явная формула требует учета поправок через функцию Мангольдта и обращение Мёбиуса.
Главный член:
$ \pi(x) = \sum_{n=1}^{\infty} \frac{\mu(n)}{n} J(x^{1/n}), \quad \text{где} \quad J(y) = \operatorname{li}(y) - \sum_{\rho} \operatorname{li}(y^{\rho}) - \log 2 + \dots $
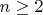
Здесь $\mu(n)$ — функция Мёбиуса. Слагаемые для $n \geq 2$ оцениваются как:
$ \sum_{n \geq 2} \frac{\mu(n)}{n} J(x^{1/n}) \ll \frac{\sqrt{x}}{\log x}. $

4. Сумма по нулям
Главный вклад в отклонение $\pi(x) - \operatorname{li}(x)$ дают нули $\rho$:
- При выполнении гипотезы Римана $\left(\operatorname{Re} \rho = \frac{1}{2}\right)$:
$ \sum_{\rho} \operatorname{li}(x^{\rho}) \ll \sqrt{x} \log x. $

Поправочные члены (константа и интеграл) имеют порядок $O(1)$, что много меньше, чем вклад нулей ($\sim \sqrt{x} \log x$).

[Yadryara]

vicvolf в сообщении #1692178 писал(а):

Поправочные члены (константа и интеграл) имеют порядок $O(1)$, что много меньше, чем вклад нулей ($\sim \sqrt{x} \log x$).

А реальный вклад нулей гораздо меньше — как уже говорил, не умножать надо на логарифм, а делить и потом умножать примерно на $0.1726$, то есть в среднем ещё почти в 6 раз меньше.

[Dmitriy40]

vicvolf
Практика показывает что главный вклад вносят $\sum_{n=1}^\infty \frac{\mu(n)}{n}\operatorname{li}(\sqrt[n]{x})$ для нескольких малых $n$, а вовсе не сумма по нулям. Посмотрите хоть на таблицу Yadryara чуть выше, даже для $x=100$ вклад первых трёх членов с li больше по абсолютной величине всего суммарного вклада суммы по нулям.

[vicvolf]

Yadryara в сообщении #1692182 писал(а):

vicvolf в сообщении #1692178 писал(а):

Поправочные члены (константа и интеграл) имеют порядок $O(1)$, что много меньше, чем вклад нулей ($\sim \sqrt{x} \log x$).

А реальный вклад нулей гораздо меньше — как уже говорил, не умножать надо на логарифм, а делить и потом умножать примерно на $0.1726$, то есть в среднем ещё почти в 6 раз меньше.

Оценка нетривиальных нулей дзета функции при условии выполнения гипотезы Римана - это теоретическая оценка в общем случае при учете всех нулей. При реальных вычислениях на каких-то интервалах оценка может значительно сильнее, как у Вас.
Помните гипотезу Мертенса - $M(n)$ ограничена $-\sqrt(n),+\sqrt(n)$. На самом деле при сравнительно небольших $n$ значения $|M(n)|$ значительно меньше, а потом вдруг скачок.....
https://ru.wikipedia.org/wiki/%D0%93%D0 ... 1%81%D0%B0