Проблема в том, что "непосредственно" эта задача смысла не имеет. Действительно, в такой наивной постановке нам следовало бы минимизировать энергию
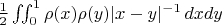
при условии
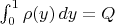
, что должно бы привести к задаче о постоянстве потенциала
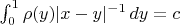
. К сожалению, все одномерные интегралы содержащие
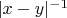
расходятся логарифмически при

. Тогда, если мы рассмотрим задачу как предел трехмерной (или двумерной) с толщиной порядка
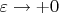
то регуляризованная таким образом энергия будет
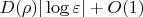
с
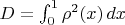
причём вне зависимости от формы тела (лишь бы оно сохраняло её утончаясь). Тогда естественно стараться минимизировать
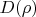
и стараться доказать что результат сходится именно к этому. Но здесь действительно минимайзером
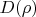
при
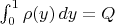
будет
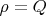
Вот резюме статьи Джексона (вообще, он же писал в том же журнале на ту тему раньше, и другие тоже).
Цитата:
The question of the equilibrium linear charge density on a charged straight conducting “wire” of finite length as its cross-sectional dimension becomes vanishingly small relative to the length is revisited in our didactic presentation. We first consider the wire as the limit of a prolate spheroidal conductor with semi-minor axis a and semi-major axis c when a/c<<1. We then treat an azimuthally symmetric straight conductor of length 2c and variable radius r(z) whose scale is defined by a parameter a. A procedure is developed to find the linear charge densityλ(z) as an expansion in powers of 1/Λ, where Λ≡ln(4c2/a2), beginning with a uniform line charge densityλ0. We show, for this rather general wire, that in the limit Λ>>1 the linear charge density becomes essentially uniform, but that the tiny nonuniformity (of order 1/Λ) is sufficient to produce a tangential electric field (of order Λ0) that cancels the zeroth-order field that naively seems to belie equilibrium. We specialize to a right circular cylinder and obtain the linear charge density explicitly, correct to order 1/Λ2 inclusive, and also the capacitance of a long isolated charged cylinder, a result anticipated in the published literature 37 years ago. The results for the cylinder are compared with published numerical computations. The second-order correction to the charge density is calculated numerically for a sampling of other shapes to show that the details of the distribution for finite 1/Λ vary with the shape, even though density becomes constant in the limit Λ→∞. We give a second method of finding the charge distribution on the cylinder, one that approximates the charge density by a finite polynomial in z2 and requires the solution of a coupled set of linear algebraic equations. Perhaps the most striking general observation is that the approach to uniformity as a/c→0 is extremely slow.