lasta:
Проверено для каких интервалов чисел?
Для любых (проще говоря - для всех чисел от - до + бесконечности)
Для уравнения

при увеличении
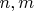
растет и к. "Ближайшие" к интересующему нас значению

(более "не приближается" а только отдаляются в одну и другую сторону) значения

и

. Трехмерные графики я приводил в своей теме "И вновь о соседних кубах..."
-- 17.06.2015, 11:21 --Добавлю, пожалуй, чтобы понятнее было:
если рассматривать просто любое число

в уравнении

, то оно действительно будет периодически и "догонять" и "перегонять"...