И ладно бы арифметический корень (имеется в виду с любым показателем) был бы всегда определен только для положительных чисел (как у Фихтенгольца например).
Я видел литературу, в которой используется как первый подход (изучаются только арифметические корни и только положительные основания дробных степеней, например, трехтомник Фихтенгольца 2003 г)
Издания 2003 г. у меня нет. Но существенных изменений в поздних изданиях быть не должно. В первом томе «Курса дифференциального и интегрального исчисления» (1947, 1962) п. 48
Цитата:
Степенная функция.
Так называется функция вида
где

— любое постоянное вещественное число. При целом

получается рациональная функция. При

дробном мы имеем радикал. Например, пусть

— натуральное число и
эта функция определена для всех значений

, если

— нечётное, и лишь для неотрицательных значений — при

четном (в этом случае мы имеем в виду арифметическое значение радикала.) Наконец, если

— иррациональное число, мы будем предполагать
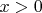
(

допускается лишь при

).
Условие положительности основания при иррациональном показателе принято во всех известных мне курсах начал анализа. Также во всех известных мне курсах при нечетном

область определения радикала — все действительные числа. Дробные степени с положительным основанием нужны при определении показательной функции. Поэтому они также есть в любом подробном курсе начал анализа. Дробные степени с отрицательным основанием — по вкусу: можно использовать суперпозицию корня и степени. Но включение дробных степеней для отрицательных значений много к объёму материала не добавляет. (Это важно только на экзаменах, но тут просто надо не ловить на мелочах студентов.
bot в
post54001.html#p54001 в этом духе писал. Ну, мелочи это всё. )
Более того, в первой теме даже понятие уравнения трактуется по разному.
Пусть дано ур-е

. Если следовать правилам равносильности и идти через

,

, то получаем корень между 1 и 2. Однако, это уравнение имеет и корень

, так как по определению корня он превращает ур-е в верное равенство. Как быть с такой "равносильностью". Может быть это в институте проходят?
Имхо,
решение уравнения с одним неизвестным — число, которое при подстановке в уравнение вместо неизвестной величины превращает уравнение в (верное) равенство. В данном случае действительное число.
При  входящие в уравнение операции (функции) определены
входящие в уравнение операции (функции) определены (опечатка). При

входящие в уравнение операции (функции) определены. Следовательно,

— решение уравнения. Как-то так. Никогда не задумывался над формализацией, может быть что-то тонкое не вижу.
Левая часть является степеннопоказательной функцией и по определению её основание положительно.
Для иррациональных показателей положительно. (Предполагаю, в связи с тем, что на первом курсе в большинстве заданий по анализу основание положительно, многие на автомате скажут, что

.)
Может быть, речь идёт о следующей процедуре "сложения":
До такого варианта я не додумался. :) Спасибо!