Цепочки близнецов
Ранее было показано (тема"Цепочки простых чисел"), что максимальное число простых чисел,
составляющих арифметические прогрессии с разностью

в общем случае не превышает

,
k некратно

.
Смысл ограничения заключается в том, что члены таких прогрессий являются вычетами ПСВ
(приведенная система вычетов) по модулю

, т.е. предыдущее цепочке число и следующее
после цепочки число будут кратны

Цепочки близнецов надо рассматривать как суперпозицию двух классов вычетов по модулю

с разностью между вычетами

и

Поэтому условимся считать разность между близнецами в цепочке с одной стороны как разность,
между вычетами суперпозиции. т.е.

и

и с другой стороны как модуль классов

.
Переходя к цепочкам близнецов необходимо учитывать, что в суперпозиции отдельные цепочки
простых чисел каждого класса не могут совпадать, поэтому совершенно очевидно, что длина
цепочек близнецов меньше длины цепочек простых чисел и при самом лучшем раскладе эти цепочки
могут не совпадать на один модуль. В этом случае цепочки близнецов будут состоять из

пар.
Пример, при
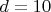
(модуль 12)

число пар в цепочке


Но цепочки с разностью

(модуль 24 - 2) число пар только 2.
Здесь мы имеем несовпадение отдельных цепочек простых чисел на два модуля.
Поэтому надо рассматривать каждый модуль цепочек отдельно.
Следует заметить, что цепочка

исключение, т.к.
первая пара имеет простое число 5 и в дальнейшем на этом месте будут числа, кратные 5.
С другой стороны цепочки близнецов надо рассматривать как группы (кортежи) вычетов
с числом вычетов в два раза большим, чем у групп (кортежей) простых чисел отдельных
классов по модулю 6к, что накладывает ограничения на проходимость таких групп (кортежей) в ПСВ.
Почему критерием существования групп (кортежей) простых чисел в натуральном ряду
является ПСВ (приведенная система вычетов) по модулю

Потому, что если данная группа не существует в ПСВ, то ее не может быть и в интервале простых
чисел этой ПСВ.
Пример 1: проверим группу из 3-х близнецов с разностью

(24 - 2)
Приведенная группа (0, 2, 24, 26, 48, 50)

Проходимость по модулю

по модулю

Таких групп нет в ПСВ и среди простых чисел.
Пример 2: при разности

возможное число пар близнецов

,
но общее число вычетов группы

т.е. проходимость такой группы надо проверять до модуля

.
Приведенная группа (0, 2, 30, 32, 60, 62, 90, 92, 120, 122)
Проходимости 1) по модулю

2) по модулю

3) по модулю

Группа (кортеж) из 5-ти пар близнецов с разностью 30 существует в любой ПСВ и среди простых чисел.
