Предположим, что на множестве

заданы две бинарные операции, которые будем называть сложением (обозначаем

) и умножением (обозначаем
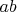
). Об этих операциях предполагаем следующее:
1)

(коммутативность сложения);
2)

(ассоциативность сложения);
3) существует такой элемент

, что

для любого

(

-
нулевой элемент);
4) для каждого

существует такой

, что

(
противоположный элемент);
5)

и

(дистрибутивность умножения относительно сложения; предполагается стандартное соглашение о порядке выполнения операций).
Множество

с такими операциями называется кольцом.
Здесь последовательно доказываем ряд утверждений.
I. Нулевой элемент единственен.Доказательство. Пусть

и

- два нулевых элемента. Тогда

.
 II. Противоположный элемент единственен.Доказательство.
II. Противоположный элемент единственен.Доказательство. Пусть

и

- два противоположных элемента для

. Тогда

.

Поскольку элемент, противоположный заданному элементу

, единственен, целесообразно ввести для него специальное обозначение:

. Таким образом,

. Поскольку в силу коммутативности

, то

.
III. Уравнение  имеет решение, и это решение единственно.Доказательство. Существование решения.
имеет решение, и это решение единственно.Доказательство. Существование решения. Проверим, что

является решением. Подставляя его в уравнение, получим

,

,

,

,

,

- верное равенство.
Единственность решения. Пусть
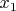
и
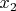
- два решения, то есть,

и

. Тогда

. Прибавляя к обеим частям равенства

слева, получим

,

,

,

,

,

.

Решение уравнения

называется
разностью элементов

и

и обозначается

. Как мы видели,

. В частности,

.
IV. Законы дистрибутивности выполняются и для разности:  и
и  .Доказательство.
.Доказательство. По определению разности,

. Умножая обе части равенства слева на

, получим

,

,
откуда, опять по определению разности,

. Аналогично доказывается второе равенство.
 V.
V.  для любого элемента
для любого элемента  .Доказательство.
.Доказательство. Пусть

. Тогда

.
Аналогично доказывается, что

.

По аналогии с вычитанием определяется и деление. Если рассматривать произвольные кольца, для которых выполняются только перечисленные выше пять аксиом, можно определить только деление слева и деление справа как решение уравнений

и

при условии, что соответствующее решение существует и единственно (мы же хотим, чтобы операция деления - пусть их даже две - давала определённый результат).
Однако, если кольцо

имеет больше одного элемента, то мы столкнёмся с тем, что уравнения

и

при

вообще не могут иметь решений, а при

имеют более одного решения. Поэтому деление на ноль оказывается невозможным, если мы хотим, чтобы оно было однозначным.
 и
и  .Доказательство.
.Доказательство. 
, поэтому

. Аналогично и

. Наконец,

.
Элемент

(соответственно,

) кольца

называется
левой единицей (соответственно,
правой единицей), если

(соответственно,

) для любого элемента

.
По аксиоме 3), кольцо обязано содержать элемент

. Других элементов оно может и не содержать.
VII. Если кольцо содержит больше одного элемента и имеет левую (правую) единицу, то эта единица не совпадает с нулём.Доказательство. Пусть

(такой элемент существует по условию),

- левая единица. Тогда

, то есть,

, откуда

. Аналогично - для правой единицы.
 VIII. Если в кольце есть и левая, и правая единицы, то они совпадают.Доказательство.
VIII. Если в кольце есть и левая, и правая единицы, то они совпадают.Доказательство. Пусть

- левая, а

- правая единица. Тогда

.

Заметим, что в этом доказательстве

- любая левая, а

- любая правая единица. Поэтому предыдущее утверждение означает, что любая левая единица совпадает с любой правой (если они существуют). Однако в кольце может быть несколько левых единиц и ни одной правой, или наоборот.
Элемент кольца называется
единицей, если он является и левой, и правой единицей.
IX. В кольце с единицей единица единственна.Доказательство. Это утверждение сразу следует из предыдущего замечания, но можно доказать и непосредственно. Пусть

и

- две единицы. Тогда

.

Тело, в дополнение к перечисленным выше аксиомам кольца, имеет ещё следующие аксиомы:
6)

(ассоциативность умножения);
7) существует такой элемент

,

, что

и

для любого

(

-
единичный элемент);
8) для каждого

,

, существует такой

, что

(
обратный элемент).
Пусть

- тело.
X. Если элемент  является обратным элементу
является обратным элементу  , то элемент
, то элемент  является обратным элементу
является обратным элементу  .Доказательство.
.Доказательство. Нам нужно доказать, что

.
Так как

, то

, поэтому по аксиоме 8) элемент

имеет обратный элемент

. Тогда

.
 XI. Обратный элемент является единственным.Доказательство.
XI. Обратный элемент является единственным.Доказательство. Пусть некоторый элемент

имеет два обратных -

и

. Тогда

.

Поскольку для заданного элемента

обратный элемент является единственным, имеет смысл ввести для него специальное обозначение:

. Таким образом,

; как только что доказано,

и

.
XII. Если  , то уравнения
, то уравнения  и
и  имеют решения, причём, эти решения единственны.Доказательство.
имеют решения, причём, эти решения единственны.Доказательство. Рассмотрим уравнение

.
Существование решения. Проверим, что

является решением. Подставляя его в уравнение, получим

,

,

,

- верное равенство.
Единственность решения. Пусть
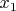
и
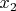
- два решения, то есть,

и

, то

. Умножая обе части этого равенства слева на

, получим

,

,

,

.
Аналогично существование и единственность решения доказываются для уравнения

. Для него получается

.

Как видим из доказательства, решения уравнений

и

при

даются формулами

и

. Это даёт для тела две операции деления на элементы, не равные

: деление слева

и деление справа

.
Наконец, поле имеет ещё одну аксиому:
9)

(коммутативность умножения).
Из этой аксиомы следует, что приведённые выше решения уравнений

и

совпадают:

. Это позволяет ввести для поля операцию деления на элементы, не равные

.
Кольцо может состоять из одного нулевого элемента, тогда он же будет и единичным. В теле и поле по аксиоме 7)

. Это требование формулируется для того, чтобы не считать полем кольцо, состоящее из одного элемента. Можно было бы потребовать, чтобы тело (поле) содержало больше одного элемента, тогда неравенство

было бы доказуемым.