Двойственность в булевой алгебре и не только

[Свободный Художник]

Профессор Снэйп писал(а):

Свободный Художник писал(а):

Так что арифметика рациональных чисел вполне может рассматриваться как раздел Computer Science

Думаю, к этому выводу можно было прийти и более простыми средствами

Это не вывод, а просто сопутствующее замечание.
Определенная выше система $\mathbf{SQ^+_{\, 0,\: \infty}}$ позволяет записывать в виде первопорядковых предложений те утверждения о системе $\mathbf{Q^+_{\, 0,\: \infty}}$, которые касаются манипуляций со строками $\varphi$ в алфавите $\{V, H\}$.
Например, следующее вспомогательное утверждение о связи операций $\blacksquare$ арифметического и $\square$ гармонического средних, которое понадобиться при дальнейшем обсуждении.

Утверждение касается связи значений операций $\blacksquare$ и $\square$, вычисленных на концах интервала, ассоциированного с данным положительным рациональным числом $x$:
$\forall \varphi \forall \psi \{\,[\varphi(1) = \psi(0) \,\blacksquare\, \psi(\infty)] \,\Rightarrow\, [\varphi(0) = \psi(0) \,\square\, \psi(\infty)]\, \}$.

По поводу “интервала, ассоциированного с данным положительным рациональным числом $x$”:

Свободный Художник писал(а):

Чтобы при формулировке “любопытного факта” не апеллировать к диаграмме с изображением Stern-Brocot Tree, можно ввести в системе $\mathbf{Q^+_{\, 0,\: \infty}}$ понятие “интервала, ассоциированного с данным положительным рациональным числом $x$”.
С интуитивной точки зрения, это – интервал, который определяется двумя числами, между которыми на соответствующем уровне дерева вставляется положительное рациональное число $x$ при своем “возникновении”.
Например, для $x = 1/3$ ассоциированный интервал будет $(0, 1/2)$; для $x = 4/7$ – интервал $(1/2, 3/5)$; для $x = 5/1$ – интервал $(4/1, \infty)$ и т. д.

Формально этот интервал можно определить следующим образом. Пусть $\varphi$ будет произвольной строкой из символов $V$ и $H$ и пусть выражение $\varphi(x)$ будет обозначать соответствующий терм, составленный из символов операций $V$ и $H$; например, выражение $VHV(x)$ будет обозначать терм $V(H(V(x))$.
Каждому положительному рациональному числу $x$ соответствует единственная строка $\varphi$, определяемая из соотношения $x = \varphi(1)$. Если длина строки $\varphi$ равна $n$, то число $x$ возникает на $n$ - ом уровне дерева, вставляясь при этом, как можно показать, между числами $\varphi(0)$ и $\varphi(\infty)$, которые и определяют “интервал $(\varphi(0), \varphi(\infty))$, ассоциированный с данным положительным рациональным числом $x$”.

При вычислении выражений $\varphi(0)$ и $\varphi(\infty)$ можно использовать следующие соотношения:
$H(0) = 1, H(\infty) = \infty, V(0) = 0, V(\infty) = 1.$

juna писал(а):

О дереве Штерна-Брока написано также в "Конкретной математике", и пока мы почти не выходим за пределы описанного там. Мне бы было интересно построить это дерево на все $\mathbb Q$.

juna, на Ваше предложение я чуть позже отвечу.

[Свободный Художник]

juna писал(а):

О дереве Штерна-Брока написано также в "Конкретной математике", и пока мы почти не выходим за пределы описанного там. Мне бы было интересно построить это дерево на все $\mathbb Q$.

Меня Stern-Brocot Tree интересует как один из способов построения рациональных точек проективной шкалы. Примерно в том духе, как описано у Ефимов Н.В. Высшая геометрия. М.: Наука, 1971, сс. 271 – 290.
http://eqworld.ipmnet.ru/ru/library/mathematics/angeometry.htm

Рисунок с первыми шагами построения этой шкалы можно посмотреть здесь:
http://lib.e-science.ru/book/143/page/279.html
(качество, правда, неважное). При построении шкалы стартуют с тройки точек $0, 1, \infty $. Поэтому меня и интересуют те “законы роста” для Stern-Brocot Tree, о которых я писал выше, ибо каждый такой закон представляет собой построение новой точки шкалы при помощи тернарной операции “построения 4-ой гармонической к данной тройке чисел”. Самая первая такая “данная тройка чисел” – это тройка $0, 1, \infty $.
Поскольку в проективной шкале строятся и отрицательные рациональные числа, то я не вижу принципиальных трудностей для обобщения Дерева на все $\mathbb Q$.
По-видимому, это будут два дерева. Одно для положительных, а другое – для отрицательных чисел. Т. е. небольшой такой лес.

Добавлено спустя 12 минут 9 секунд:

Кстати говоря, материал по Дереву имеется и здесь:
М. Айгнер, Г. Циглер.
Доказательства из Книги. Лучшие доказательства со времен Евклида до наших дней, сс. 106 -- 110.
http://dxdy.ru/topic7433-30.html

[juna]

Свободный Художник в сообщении #174852 писал(а):

Поскольку в проективной шкале строятся и отрицательные рациональные числа, то я не вижу принципиальных трудностей для обобщения Дерева на все .
По-видимому, это будут два дерева. Одно для положительных, а другое – для отрицательных чисел. Т. е. небольшой такой лес.

Мой интерес связан с установлением на множетсве $\mathbb Q$ не совсем естественного порядка. см.
http://dxdy.ru/topic18777.html
http://dxdy.ru/topic7682.html
Пусть $a$ предшествует $b$, если $\frac{-1}{a}<\frac{-1}{b}$.
Из этого определения следует, что положительные числа предшествуют отрицательным, т.е. в некотором смысле $0$ - самое минимальное число, $-1$ - самое максимальное.
Если принять это определение, то при построении дерева Штерна-Брока не будет никакого леса:
$\frac{0}{1}------------------------\frac{1}{-1}$
$\frac{0}{1}------------\frac{1}{0}-----------\frac{1}{-1}$
$\frac{0}{1}-----\frac{1}{1}------\frac{1}{0}------\frac{2}{-1}----\frac{1}{-1}$
$\frac{0}{1}--\frac{1}{2}--\frac{1}{1}---\frac{2}{1}--\frac{1}{0}---\frac{3}{-1}--\frac{2}{-1}--\frac{3}{-2}-\frac{1}{-1}$
и т.д.
Таким образом, слева восстанавливается стандартное дерево Штерна-Брока для $\mathbb Q^+$, а справа получаем его для $\mathbb Q^-$, но с дырами.

[Свободный Художник]

juna писал(а):

Пусть $a$ предшествует $b$, если $\frac{-1}{a}<\frac{-1}{b}$.
Из этого определения следует, что положительные числа предшествуют отрицательным, т.е. в некотором смысле $0$ - самое минимальное число, $-1$ - самое максимальное.
Если принять это определение, то при построении дерева Штерна-Брока не будет никакого леса:

Да, интересное упорядочение. Я подумаю. Одна мысль по его поводу вертится, но сегодня поздно уже.

[juna]

Интересного пока мало потому, что правая половина с дырами. Лучше стандартное построение на трех листах
$\frac{-1}{0}---\frac{0}{1}---\frac{1}{0}$
или нестандартное, но тоже на трех листах:
$\frac{0}{1}---\frac{1}{-1}---\frac{0}{-1}$

[Свободный Художник]

Свободный Художник писал(а):

juna писал(а):

О дереве Штерна-Брока написано также в "Конкретной математике", и пока мы почти не выходим за пределы описанного там. Мне бы было интересно построить это дерево на все $\mathbb Q$.

Кстати говоря, материал по Дереву имеется и здесь:
М. Айгнер, Г. Циглер.
Доказательства из Книги. Лучшие доказательства со времен Евклида до наших дней, сс. 106 -- 110.
http://dxdy.ru/topic7433-30.html

Вообще, с деревьями хорошо бы не запутаться.
Например, в “Конкретной математике”:
Грэхем Р., Кнут Д., Паташник О.
Конкретная математика. Основание информатики, М., Мир, 1998
на с. 141 в качестве Stern-Brocot Tree приведено то же самое дерево, что и по ссылкам:
http://mathworld.wolfram.com/Stern-BrocotTree.html
http://www.cut-the-knot.org/blue/Stern.shtml
http://en.wikipedia.org/wiki/Stern-Brocot_tree

Тогда как у М. Айгнер, Г. Циглер. Доказательства из Книги. Лучшие доказательства со времен Евклида до наших дней, на с. 106 в контексте обсуждения одной работы Мориса Абрахама Штерна приведено уже другое дерево.
Понятно, что оба эти дерева (в “Конкретной математике” и у Айгнера) тесно связаны друг с другом, но все же это – разные деревья.
Чтобы различать их, я предлагаю называть то дерево, что у Айгнера – “поверхностным”, поскольку оно самым непосредственным образом индуцируется операторами $V$ и $H$:

Свободный Художник писал(а):

Свободный Художник в сообщении #144875 писал(а):

Например, для $\mathbf{Q^+}$ являются справедливыми, очевидно, следующие два утверждения:
(1) Существует элемент, удовлетворяющий условию $\overline{x} = x$;
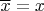
(2) Такой элемент единственен.
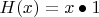
Положив этому элементу естественное имя 1, мы можем определить две двойственные друг по отношению к другу унарные операции: $H(x) = x \bullet 1$ и $V(x) = x \circ 1$.
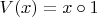
Затем при помощи этих двух унарных операций H и V, примененных в различных комбинациях к 1, мы, как можно показать, можем получить все положительные рациональныечисла, причем разным комбинациям будут соответствовать разные числа.
Например, $V(H(H(1))) = 3/4$

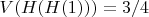
Кстати говоря, система с двумя унарными операциями $V$ и $H$, основанная на системе $\mathbf{Q^+}$, также весьма интересна (обозначим ее $\mathbf{SBT}$):
$\mathbf{SBT} =\: <\! \mathrm{SBT}, V, H, 1>$,
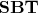
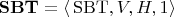
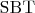
где $\mathrm{SBT}$ есть снова множество положительных рациональных чисел;
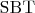
$V$ и $H$ есть унарные операции на множестве $\mathrm{SBT}$, определяемые как указано выше;
$1$ есть выделенный элемент во множестве $\mathrm{SBT}$.

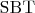
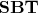
Во-первых, $\mathbf{SBT}$ есть абсолютно свободная алгебра с двумя унарными операциями и одним выделенным элементом;
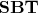
во-вторых, система $\mathbf{SBT}$ может служить основой для анализа различных соотношений, возникающих в контексте Stern-Brocot Tree
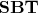
(аббревиатура $\mathbf{SBT}$ для системы выбрана в честь этого деревца).

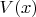
Т. е., если некоторая вершина “поверхностного” дерева помечена положительным рациональным числом $x$, то левый сын этой вершины будет помечен числом $V(x)$, а правый сын будет помечен числом $H(x)$.

То дерево, которое приведено в “Конкретной математике” на с. 141 связано с операторами $V$ и $H$ более опосредованным образом, поэтому я предлагаю называть его “глубинным” или просто “Stern-Brocot Tree”. В контексте определенной выше системы $\mathbf{SQ^+_{\, 0,\: \infty}}$ эту связь можно описать следующим образом:

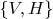
пусть некоторая вершина Stern-Brocot Tree помечена положительным рациональным числом $x$ и пусть $\varphi$ будет строкой в алфавите $\{V, H\}$, определяемой из соотношения $x = \varphi(1)$. Тогда левый сын этой вершины будет помечен числом $(\varphi V)(x)$, а правый сын будет помечен числом $(\varphi H)(x)$.
На странице:
http://www.px-pict.com/10/4/4/5.html
оба дерева (дорощенные до 4-го уровня) нарисованы рядышком, чтобы было удобнее их сравнивать.

[Свободный Художник]

Свободный Художник писал(а):

... естественно расширить систему $\mathbf{Q^+_{\, 0,\: \infty}}$, заставив действовать на ее множестве-носителе $\mathrm{Q^+_{\, 0,\: \infty}} = \mathrm{Q^+} \cup \{0, \infty \}$ свободную полугруппу строк
$\mathbf{S_{\, V,\: H}} =\: <\!\{V, H\}^+,\, \cdot >$,
где $\{V, H\}^+$ есть множество всех строк в алфавите $\{V, H\}$,
$\cdot$ есть операция конкатенации строк (которую при записи термов будем, как правило, опускать).

Т. е. расширить систему $\mathbf{Q^+_{\, 0,\: \infty}}$ до системы
$\mathbf{SQ^+_{\, 0,\: \infty}} =\: <\!\mathbf{S_{\, V,\: H}} \,,\: \mathbf{Q^+_{\, 0,\: \infty}}\,, \: *\, >$,
где $*$ есть операция “действия”:
для любых чисел $x, y$, принадлежащих $\mathrm{Q^+_{\, 0,\: \infty}}$ и для любой строки $\varphi$, принадлежащей $\{V, H\}^+$,
запись $y = \varphi * x$ означает, что число $y$ является результатом действия строки $\varphi$ на число $x$.

Смысл операции $*$ действия определяется смыслом определенных в предыдущих постах операторов $V$ и $H$; например, если $x = 2/3$ и $\varphi = HV$, то $\varphi * x = HV*(2/3) = H(V(2/3)) = 7/5$.
Далее вместо $y = \varphi * x$ будем также писать $y = \varphi(x)$.

Двойственность в системе $\mathbf{SQ^+_{\, 0,\: \infty}}$ (или в системе $\mathbf{SR^+_{\, 0,\: \infty}}$) естественно связать с двойственностью в электротехнике:
http://en.wikipedia.org/wiki/Duality_(electrical_circuits),
поскольку система $\mathbf{SQ^+_{\, 0,\: \infty}}$ (или $\mathbf{SR^+_{\, 0,\: \infty}}$) допускает естественную “электротехническую” интерпретацию.

Действительно, отметим прежде всего, что система $\mathbf{SQ^+_{\, 0,\: \infty}}$ -- это “двухсортная” система, в которой имеются объекты двух сортов: строки символов в алфавите $\{V, H\}$ и числа из $\mathrm{Q^+_{\, 0,\: \infty}} = \mathrm{Q^+} \cup \{0, \infty \}$ (аналогично тому, как в векторных пространствах имеются объекты двух сортов: скаляры и векторы).

При электротехнической интерпретации мы интерпретируем строки символов в алфавите $\{V, H\}$ как “четырехполюники”, а числа из $\mathrm{Q^+_{\, 0,\: \infty}} = \mathrm{Q^+} \cup \{0, \infty \}$ -- как “двухполюсники” (число $x$ из $\mathrm{Q^+_{\, 0,\: \infty}}$ интерпретируется как сопротивление соответствующего двухполюсника, в частности, $0$ интерпретируется как двухполюсник короткого замыкания, а $\infty$ -- как двухполюсник холостого хода).

Операция $\bullet$ интерпретируется как операция последовательного соединения двухполюсников,
операция $\circ$ интерпретируется как операция параллельного соединения двухполюсников,

выражение $\varphi * x = \varphi(x)$ с фундаментальной для системы $\mathbf{SQ^+_{\, 0,\: \infty}}$ операцией $*$ “действия” интерпретируется как четырехполюсник $\varphi$, нагруженный на сопротивление $x$;
в частности $\varphi(0)$ обозначает четырехполюсник $\varphi$ в режиме короткого замыкания, а выражение $\varphi(\infty)$ -- четырехполюсник $\varphi$ в режиме холостого хода.
-------------------------------

Оказывается, такого рода “алгебры двухполюсников и четырехполюсников” активно изучались:

Шестаков В. И. Алгебра двухполюсных схем, построенных исключительно из двухполюсников (алгебра А-схем)//Автоматика и телемеханика, 1941, № 2. — С. 15-24.
(об этой работе см.. в Бажанов В. А.
В.И. Шестаков и К. Шеннон. Разные судьбы творцов одной красивой идеи // Вопросы истории естествознания и техники, 2005, № 2. С. 112—121:
http://www.ulsu.ru/staff/homepages/bazhanov/russian/Viet_Shes05.pdf)

Телешев Юрий Владимирович
Алгебры пассивных двухполюсников:
http://ito.edu.ru/2000/II/3/391.html

[Свободный Художник]

Свободный Художник писал(а):

Оказывается, такого рода “алгебры двухполюсников и четырехполюсников” активно изучались:
Шестаков В. И. Алгебра двухполюсных схем, построенных исключительно из двухполюсников (алгебра А-схем)//Автоматика и телемеханика, 1941, № 2. — С. 15-24.
(об этой работе см.. в Бажанов В. А.
В.И. Шестаков и К. Шеннон. Разные судьбы творцов одной красивой идеи // Вопросы истории естествознания и техники, 2005, № 2. С. 112—121:
http://www.ulsu.ru/staff/homepages/bazhanov/russian/Viet_Shes05.pdf)

Телешев Юрий Владимирович
Алгебры пассивных двухполюсников:
http://ito.edu.ru/2000/II/3/391.html

В цитированной работе Бажанова В. А. на сс. 92 – 94 (сс. 3 – 5 pdf-файла) приводится информация об “алгебре двухполюсных схем” В. И. Шестакова. Как я понял, эта алгебра изоморфна обсуждавшейся выше системе $\mathbf{Q^+_{\, 0,\: \infty}}$:

Свободный Художник писал(а):

вздымщик Цыпа писал(а):

Предлагаю пополнить $\mathrm{Q^+}$ ($\mathrm{R^+}$) элементами $0$ и $\overline{0}$
$x \bullet 0 = x$
$x \circ 0 = 0$
$x \circ \overline{0} = x$
$x \bullet \overline{0} = \overline{0}$

Уж лучше вместо $\overline{0}$ ввести новый выделенный элемент $\infty$. Красивше будет.
Да и по смыслу подходит.
$x \bullet 0 = x\,, \; x \circ \infty = x \,;$
$x \bullet \infty = \infty\,, \; x \circ 0 = 0 \,;$
$\overline{0} = \infty\,, \; \overline{\infty} = 0\,;$
$\overline{1} = 1\,.$
$0$ двойственен $\infty$. $1$ самодвойственна.

Свободный Художник писал(а):

... элементы $0$ и $\infty$ -– не определимы в $\mathbf{Q^+}$, поэтому, если мы хотим говорить о них, то должны явно добавить их в сигнатуру системы, что, пользуясь случаем, я и делаю:

$\mathbf{Q^+_{\, 0,\: \infty}} =\: <\! \mathrm{Q^+}, \bullet\,, \circ\,, \overline{\phantom{a}}\,, 0\,, \infty >$

И, естественно, добавить еще аксиомы вида:
$x \bullet 0 = x\,, \; x \circ \infty = x \,;$
$x \bullet \infty = \infty\,, \; x \circ 0 = 0 \,;$
$\overline{0} = \infty\,, \; \overline{\infty} = 0\,;$
Здесь мы действительно добавили “новое” в $\mathbf{Q^+}$, поэтому и $\mathbf{Q^+_{\, 0,\: \infty}}$ -- новая система по отношению к $\mathbf{Q^+}$.

[juna]

Кстати, в этой статье рассматриваются такие законы дистрибутивности:
$x\circ (y\bullet z)\leqslant (x\circ y)\bullet (x \circ z)$
$x\bullet (y\circ z)\geqslant (x\bullet y)\circ (x \bullet z)$
и отмечается, что сама операция $\circ$ не является самостоятельной, т.к. вводится через инверсию:
$x\circ y=\overline\left (\overline x \bullet \overline y \right )$.
Т.е. по сути мы изучаем свойства алгебры с одной унарной и одной бинарной операцией.
P.S. интересно было бы взглянуть на работы Волгина Л.И., чтобы не изобретать велосипед.

[Свободный Художник]

juna писал(а):

Кстати, в этой статье рассматриваются такие законы дистрибутивности:
$x\circ (y\bullet z)\leqslant (x\circ y)\bullet (x \circ z)$
$x\bullet (y\circ z)\geqslant (x\bullet y)\circ (x \bullet z)$
и отмечается, что сама операция $\circ$ не является самостоятельной, т.к. вводится через инверсию:
$x\circ y=\overline\left (\overline x \bullet \overline y \right )$.
Т.е. по сути мы изучаем свойства алгебры с одной унарной и одной бинарной операцией.
P.S. интересно было бы взглянуть на работы Волгина Л.И., чтобы не изобретать велосипед.

Да, согласен.
Вы меня опередили с постом про дистрибутивность.
Но раз уж написал, то приведу.

Профессор Снэйп писал(а):

Забавная алгебраическая система, я раньше с подобным не встречался.

Боюсь, что тождества $\overline{x \bullet y} = \overline{x} \circ \overline{y}$, $\overline{x \circ y} = \overline{x} \bullet \overline{y}$ и $\overline{\overline{x}} = x$ --- это единственное, что есть общего у полученной системы с алгеброй множеств (не считая довольно часто встречающихся коммутативности и ассоциативности бинарных операций). Прежде всего нет идемпотентности, то есть $x \bullet x \neq x \neq x \circ x$, а идемпотентность --- одно из самых характерных свойств теоретико-множественных операций, задающее их уникальную специфику. Далее, отсутствуют нейтральные элементы, то есть ни для какого $e \in \mathrm{Q^+}$ не выполняются тождества $x \bullet e = x$, $x \circ e = x$. Наконец, не выполняется ни одно из тождеств дистрибутивности: $x \circ (y \bullet z) = (x \circ y) \bullet (x \circ z)$, $x \bullet (y \circ z) = (x \bullet y) \circ (x \bullet z)$. Так что с утверждением

Свободный Художник писал(а):

...в системе $\mathbf{Q^+}$ будут справедливы многие законы, имеющие место быть в булевой алгебре...

я, пожалуй, не соглашусь. Больше всего мне здесь не нравится слово "многие"

В. А. Бажанов (с. 4 pdf-файла) утверждает, что в “алгебре двухполюсных схем” В. И. Шестакова справедливы “субдистрибутивный” и “супрадистрибутивный” законы, которые в нашей нотации запишутся следующим образом:
$x\circ (y\bullet z) \le (x\circ y) \bullet (x\circ z)$ -- субдистрибутивный закон;
$x\bullet (y\circ z) \ge (x\bullet y) \circ (x\bullet z)$ -- супрадистрибутивный закон.

Я проверил субдистрибутивный закон. Выполняется.

[juna]

На $\mathbb Q^+$ выполняются оба.
Нагуглил:
www.zstu.zaporizhzhe.ua/base/news2005/9 ... 00_2_2.pdf

[Свободный Художник]

juna писал(а):

P.S. интересно было бы взглянуть на работы Волгина Л.И., чтобы не изобретать велосипед.

Просмотрел работы:

Шестаков В. И. Алгебра двухполюсных схем, построенных исключительно из двухполюсников (алгебра А-схем)// Журнал техн. физики, 1941, Т.11, № 6. — С. 532—549.
Волгин Л. И. Определение сопротивлений и проводимостей двухполюсников логико-алгебраическим методом// Электричество, 1998, № 7. — сс. 64—69.
Волгин Л. И. Субдистрибутивный и супрадистрибутивный законы логики исчисления иммитансов электрических двухполюсников// Электричество, 2001, № 2. — сс. 66—67.

Основные выводы следующие.
В работе Шестакова В. И. определяется алгебраическая система, изоморфная рассматриваемой здесь системе $\mathbf{Q^+_{\, 0,\: \infty}}$. Относительно нее устанавливаются только самые элементарные законы типа ассоциативности и коммутативности операций $\bullet$ и $\circ$, инволютивность операции обращения, законы де Моргана и связь операций $\bullet$ и $\circ$, с элементами $\{0, \infty \}$.
Формулируется также принцип двойственности и устанавливается, что подсистема системы $\mathbf{Q^+_{\, 0,\: \infty}}$, порожденная элементами $\{0, \infty \}$ изоморфна двухэлементной булевой алгебре.

В работах Волгина Л. И. единственное существенное новшество по сравнению с работой Шестакова В. И. я усматриваю в доказательстве для системы $\mathbf{Q^+_{\, 0,\: \infty}}$ субдистрибутивного и супрадистрибутивного законов:
$x\circ (y\bullet z) \le (x\circ y) \bullet (x\circ z)$ -- субдистрибутивный закон;
$x\bullet (y\circ z) \ge (x\bullet y) \circ (x\bullet z)$ -- супрадистрибутивный закон.
Кроме того, в последней работе Волгина Л. И. операция $\circ$ ошибочно соотнесена с операцией гармонического среднего.

Добавлено спустя 2 часа 13 минут 4 секунды:

Свободный Художник писал(а):

Итак, будем считать, что умножение в $\mathbf{Q^+}$ мы определили. Теперь мы в состоянии определить в $\mathbf{Q^+}$ еще две двойственные операции, которые ранее пробовались на роль основных (я буду писать $\blacksquare$ вместо $\bullet$ и $\square$ вместо $\circ$):

Профессор Снэйп писал(а):

juna писал(а):

Вы правы, так будет даже идемпотентность
$x \bullet y=\frac{x+y}{2}$

Да, при

$$ x \bullet y = \frac{x+y}{2} \text{ и } x \circ y = \frac{2xy}{x+y} $$

идемпотентность будет. Но дистрибутивности всё равно не будет

$x \,\blacksquare\, y = (x \bullet y) \cdot V(1)$;
$x \,\square\, y = (x \circ y) \cdot H(1)$.

$\blacksquare$ и $\square$ -- хорошие такие операции (арифметическое и гармоническое средние), которые, как мы видим, являются двойственными друг по отношению к другу в системе $\mathbf{Q^+}$.

Кажется, для операций $\blacksquare$ и $\square$ арифметического и гармонического средних субдистрибутивный и супрадистрибутивный законы в системе $\mathbf{Q^+_{\, 0,\: \infty}}$ также выполняются.
$x\,\square\, (y\,\blacksquare\, z) \le (x\,\square\, y)\, \blacksquare\, (x\,\square\, z)$ -- субдистрибутивный закон;
$x\,\blacksquare\, (y\,\square\, z) \ge (x\,\blacksquare\, y)\, \square\, (x\,\blacksquare\, z)$ -- супрадистрибутивный закон.

В системе $\mathbf{Q^+}$ эти законы точно выполняются.
Жаль, что операции $\blacksquare$ и $\square$ не ассоциативны. Ведь в противном случае, с учетом их идемпотентности, почти дистрибутивная решетка получалась бы.

[Свободный Художник]

Свободный Художник писал(а):

В работах Волгина Л. И. единственное существенное новшество по сравнению с работой Шестакова В. И. я усматриваю в доказательстве для системы $\mathbf{Q^+_{\, 0,\: \infty}}$ субдистрибутивного и супрадистрибутивного законов:
$x\circ (y\bullet z) \le (x\circ y) \bullet (x\circ z)$ -- субдистрибутивный закон;
$x\bullet (y\circ z) \ge (x\bullet y) \circ (x\bullet z)$ -- супрадистрибутивный закон.

Мы могли бы назвать справедливые в системе $\mathbf{Q^+_{\, 0,\: \infty}}$ субдистрибутивный и супрадистрибутивный законы “квазидистрибутивными законами”, поскольку в них вместо равенств используются отношения $\le$ и $\ge$.
Но ведь в системе $\mathbf{Q^+_{\, 0,\: \infty}}$ для операций $\bullet$ и $\circ$ справедливы также и “квазиидемпотентные законы”:
$x \le x\bullet x$ -- квазиидемпотентный закон для $\bullet$;
$x \ge x\circ x$ -- квазиидемпотентный закон для $\circ$.
-----------------------

Быть может, этих “квази” законов (вместо “полноценных” законов с равенством) булет уже достаточно для того, чтобы доказать “теорему о представлении” для системы $\mathbf{Q^+_{\, 0,\: \infty}}$, которая была бы аналогична “теореме о представлении” для булевых алгебр?

В булевой алгебре точками ее пространства представления можно считать ее двузначные гомоморфизмы, поскольку они находятся во взаимно-однозначном соответствии с ее максимальными идеалами (равно как и с ее максимальными фильтрами).
(Сикорский Р. Булевы алгебры, Мир, 1969, с. 32, с. 40).

Что из себя представляют двузначные гомоморфизмы системы $\mathbf{Q^+_{\, 0,\: \infty}}$? Определим двухэлементную булеву алгебру $\mathbf{B_2}$ в виде:
$\mathbf{B_2} =\: <\! \{0, \infty \}, \bullet\,, \circ\,, \overline{\phantom{a}}\,, 0\,, \infty >$
(очевидно, здесь $\bullet$ играет роль операции объединения, а $\circ$ играет роль операции пересечения).

$\mathbf{Q^+_{\, 0,\: \infty}}$ и $\mathbf{B_2}$ имеют одну и ту же сигнатуру, следовательно, можно говорить о гомоморфизмах из $\mathbf{Q^+_{\, 0,\: \infty}}$ в $\mathbf{B_2}$, которые и будем называть двузначными гомоморфизмами системы $\mathbf{Q^+_{\, 0,\: \infty}}$.

Теперь для каждого двузначного гомоморфизма системы $\mathbf{Q^+_{\, 0,\: \infty}}$ хотелось бы определить ассоциированные с ним максимальный идеал и максимальный фильтр системы $\mathbf{Q^+_{\, 0,\: \infty}}$.

Добавлено спустя 1 час 11 минут 55 секунд:

Нет, не получится.
Слишком мало в $\mathbf{Q^+_{\, 0,\: \infty}}$ будет двузначных гомоморфизмов.
Нетривиальных только два – в зависимости от того, куда гомоморфизм переводит $1$: в $0$ или в $\infty $.

[juna]

Свободный Художник писал(а):

Понятно, что оба эти дерева (в “Конкретной математике” и у Айгнера) тесно связаны друг с другом, но все же это – разные деревья.

Для дерева из Айгнера есть название Calkin-Wilf Tree

[Свободный Художник]

juna писал(а):

Для дерева из Айгнера есть название Calkin-Wilf Tree

OK. Принял к сведению.
Однако, чтобы получить “граф состояний автомата”, ассоциированный с системой $\mathbf{SQ^+_{\, 0,\: \infty}}$ (рассматриваемой как некоторый “автомат”), нужно к Calkin-Wilf Tree дорисовать еще две вершины и четыре дуги.
http://www.px-pict.com/10/4/4/7.html

Т. е. этот автомат не является “моногенным” по терминологии Лаллеман Ж.
Полугруппы и комбинаторные приложения. М., Мир, 1985, сc. 174 — 177.
http://www.px-pict.com/9/5/2/3/1.html

На самом деле для автомата $\mathbf{SQ^+_{\, 0,\: \infty}}$ важны все три “выделенные” состояния: $0 = 0/1,\; 1 = 1/1,\; \infty = 1/0$, поскольку многие важные предложения о системе $\mathbf{SQ^+_{\, 0,\: \infty}}$ предполагают какое-то соотнесение между собой состояний, достижимых из каждого “выделенного” состояния.
В качестве простого примера такого предложения можно привести следующее:
$\forall \varphi \{\,[\varphi(0) < \varphi(1)]\, \& \,[\varphi(1) < \varphi(\infty)]\, \}$
(оно легко доказывается индукцией по длине цепочки $\varphi$).