Доказать несчётность отрезка теоремой Бэра

[cxzbsdhwert]

warlock66613 в сообщении #1713456 писал(а):

Один и тот же интервал в пересечении с одним и тем же отрезком имеет ровно одну точку пересечения и в то же время не меньше двух точек пересечения. Это противоречие.

А на основании чего сделан вывод "и в то же время не меньше двух точек пересечения"?

[skobar]

cxzbsdhwert в сообщении #1713459 писал(а):

А на основании чего сделан вывод "и в то же время не меньше двух точек пересечения"?

Ура! Появился осмысленный вопрос :)
Попробуйте попересекать (замкнутый) отрезок $[a,b]$ c (открытым) интервалом $(c,d)$. Вы быстро убедитесь, что если пересечение непусто, то в нем будет бесконечно много точек (о чем вам и вещал лектор).

[warlock66613]

cxzbsdhwert в сообщении #1713459 писал(а):

А на основании чего сделан вывод "и в то же время не меньше двух точек пересечения"?

Предополагается, что это очевидное свойство отрезка. Его легко доказать рассмотрев, например, все различные взаиморасположения отрезка и интервала. Например, если левый край отрезка левее правого края интервала, то правый край отрезка должен быть правее левого края интервала -- иначе они вообще не будут пересекаться. И тогда любая точка между левым краем интервала и правым краем отрезка будет точкой пересечения.

[cxzbsdhwert]

skobar в сообщении #1713372 писал(а):

Пусть отрезок $[a,b], a<b$ счётен, тогда $[a,b]=\cup_{n} \{x_n\}$, то есть отрезок представлен в виде объединения счетного числа одноточечных множеств.

Перечитал ещё раз Ваше первое сообщение, я понял в чём проблема.

В основе Вашего и Лектора рассуждения лежит импликация - если множество $X$ нбчс, то оно равно, подчёркиваю - РАВНО, объединению нбчс набора одноточечных множеств $X_1,X_2,...$, где $X_n$ - одноточечное множество.
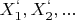
$X$ также равно объединению нбчс набора неодноточечных множеств $X^{`}_{1},X^{`}_{2},...$. Все эти объединения между собой равны.
То есть получается эдакое отношение эквивалентности между наборами, но, внимание - по критерию равенства их объединения некоторому $X$.

Если необходимо что-то доказать опираясь на эквивалентность по критерию равенства объединений, то действительно достаточно доказать утверждение используя, например однточечный набор, потому что с точки зрения объединения остальные набора эквивалентны одноточечному.
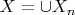
Например, если нужно доказать что $X=\emptyset$, зная что $X=\cup X_n$, то достаточно доказать для $\cup X_N$.

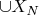
Но нас интересует другое отношение эквивалентности.
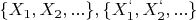
Объединения наборов $\{X_1,X_2,...\},\{X^{`}_{1},X^{`}_{2},...\}$ равны.
Нас, по теореме Бэра, интересует не объединения наборов, а сами наборы.
Нас интересует есть ли такой набор, что объединение его элементов, разумеется, равно $X$, И пересечение некоторого интервала с $X$, состоящее из более одной точки принадлежит элементу $X_n$ такого набора.
И с этой точки зрения, эквивалентность по критерию равенства объединения такого набора, если мы его нашли, объединению другого, не означает эквивалентности по критерию иметь такое $X_n$, чтобы пересечение интервала лежало в нём и имело более одной точки.

skobar в сообщении #1713372 писал(а):

Пусть отрезок $[a,b], a<b$ счётен, тогда $[a,b]=\cup_{n} \{x_n\}$, то есть отрезок представлен в виде объединения счетного числа одноточечных множеств.

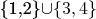
И тогда из верной импликации: "если множество нбчс, то равно объединению нбчс набора одноточечных", сделана неверная импликация: "то есть отрезок представлен в виде объединения счетного числа одноточечных множеств", то есть "если множество нбчс, то оно представлено в виде объединения нбчс набора одноточечных" - это ложная импликация. Контрпример: \{1,2\}\cup\{3,4\}$, - нбчс, но оно не представлено в виде объединения одноточечных.

Таким образом нбчс множество одновременно равно И объединению нбчс набора одноточечных И объединению нбчс набора не одноточечных.
Но, нбчс множество не представимо одновременно И в виде объединения нбчс набора одноточечных И в виде объединения нбчс набора не одноточечных.
Одно нбчс множество представимо ИЛИ в виде объединения нбчс набора одноточечных ИЛИ в виде объединения нбчс набора не одноточечных.

warlock66613 в сообщении #1713456 писал(а):

Один и тот же интервал в пересечении с одним и тем же отрезком имеет ровно одну точку пересечения и в то же время не меньше двух точек пересечения. Это противоречие.

Поэтому один и тот же интервал не с одним и тем же отрезком имеет разное количество пересечений, а, и не с одним, а с разными элементами его представлений. А с самим отрезком, как и с каждым из объединений этих разных представлений, он имеет одно и то же количество пересечений. У разных элементов разных представлений разное количество пересечений, а не у самих представлений (объединения этих элементов). И никаких тут противоречий не выходит.

Таким образом - пересечение интервала с отрезком состоит из более одной точки. Полагая отрезок нбчс - существует такой нбчс набор нбчс множеств, что объединение такого набора равно отрезку, и одно из множеств этого набора содержит пересечение с отрезком в количестве более одной точки. Тот факт, что существует другое представление не приводит к противоречиям, потому что это другое представление, потому что его элементы (множества) отличаются от элементов этого представления. Это разные наборы множеств, объединение которых, тем не менее, одинаковые.


А противоречие, рассуждая что отрезок нбчс, не в том что по теореме Бэра отрезок не представим в виде такого объединения нбчс набора $F_n$, чтобы в одном из них лежало пересечение интервала с более чем одной точкой - потому что это не так - отрезок в таком виде представим.
Противоречие в том, что такое пересечение, полностью лежащее в $F_n$ более чем с одной точкой, тем не менее, не содержит иррациональных точек, а следовательно и $F_n$ их не содержит, а следовательно объединение таких $F_n$ не будет в полной мере равно отрезку, потому что отрезок по определению это все числа из $\mathbb R$, включая иррациональные, лежащие в некотором промежутке.

[Mikhail_K]

cxzbsdhwert в сообщении #1713468 писал(а):

то есть "если множество нбчс, то оно представлено в виде объединения нбчс набора одноточечных" - это ложная импликация.

Нет, это верная импликация. Разве что, вместо слова "представлено" следует использовать слово "представимо". Я об этом уже говорил вот здесь:

Mikhail_K в сообщении #1713419 писал(а):

Не более чем счётные множества - это в точности то же самое, что объединения не более чем счётных наборов одноточечных множеств. Если $M$ не более чем счётно, то оно $M=\bigcup\limits_{x\in M}\{x\}$ есть не более чем счётное объединение одноточечных.

cxzbsdhwert в сообщении #1713468 писал(а):

Контрпример: $\{1,2\}\cup\{3,4\}$, - нбчс, но оно не представлено в виде объединения одноточечных.

Не представлено, но представимо: $\{1,2\}\cup\{3,4\}=\{1,2,3,4\}=\{1\}\cup\{2\}\cup\{3\}\cup\{4\}$. Вообще, "представлено" - это непонятно что такое, ведь для математического объекта неважно, как мы его записываем; а "представимо" - это понятно что такое.

Можно вместо слова "представимо" использовать слово "является". Ваше множество $\{1,2\}\cup\{3,4\}$ является объединением некоторого нбсч набора одноточечных - а именно $\{1\}\cup\{2\}\cup\{3\}\cup\{4\}$ - а как это Ваше множество исходно было записано, совсем неважно.

[skobar]

cxzbsdhwert в сообщении #1713468 писал(а):

если множество $X$ нбчс, то оно равно, подчёркиваю - РАВНО, объединению нбчс набора одноточечных множеств $X_1,X_2,...$, где $X_n$ - одноточечное множество.

Совершенно верно.

cxzbsdhwert в сообщении #1713468 писал(а):

$X$ также равно объединению нбчс набора неодноточечных множеств $X^{`}_{1},X^{`}_{2},...$.

Возможно, но это нас совершенно не касается, и это нам не нужно для доказательства.

cxzbsdhwert в сообщении #1713468 писал(а):

То есть получается эдакое отношение эквивалентности между наборами, но, внимание - по критерию равенства их объединения некоторому $X$.

Напридумывать можно много чего, но, ещё раз, это совершенно лишнее. Зачем вы пытаетесь встроить в доказательство что-то совершенно ненужное?

[cxzbsdhwert]

skobar в сообщении #1713471 писал(а):

Напридумывать можно много чего, но, ещё раз, это совершенно лишнее. Зачем вы пытаетесь встроить в доказательство что-то совершенно ненужное?

Не лишнее и не ненужное. Почему - написано дальше в сообщении. Давайте будем более конструктивны. Если в моём сообщении, показывающем противоречие в Ваших рассуждениях, есть противоречие, пожалуйста укажите на него, и докажите что и чему оно противоречит.

[warlock66613]

cxzbsdhwert в сообщении #1713468 писал(а):

Поэтому

Нет, никаких "поэтому". Мы конкретно доказываем, что некоторый отрезок и некоторый интервал имеют ровно одну точку пересечения. Это утверждение о самом отрезке, никаких "представлений" и "элементов представлений" в нём не упоминается.

[cxzbsdhwert]

Mikhail_K в сообщении #1713470 писал(а):

следует использовать слово "представимо"

Вот здесь полностью с Вами согласен. Как я уже писал, логику систематически я не изучал, но предположу что это называется "квантор".
Давайте тогда определимся что это за квантор такой "представимо" (не я его ввёл).
Представление в данном узком смысле - равное $F$, объединение набора множеств. Если набор множеств разный, то это разное представление, но одного и того же $F$. И тогда "представимо" значит что есть такой набор, что его объединение равно.

Mikhail_K в сообщении #1713470 писал(а):

Можно вместо слова "представимо" использовать слово "является"

А вот это снова не правильно. $\{1,2\}\cup\{3,4\}$ - представимо в виде объединения одноточечных, но не является таковым.

Mikhail_K в сообщении #1713470 писал(а):

как Ваше множество исходно было записано, совсем неважно.

Да в том то и дело что по теореме Бэра важно, потому что в теореме Бэра как раз учитывается представление $F$. Составные $F_n$ разных представлений, объединения которых, тем не менее одинаковы, имеют разное количество точек пересечений с одним и тем же отрезком.
А полагать это не важным приводит к логической ошибке которую уже допустили:

warlock66613 в сообщении #1713456 писал(а):

Один и тот же интервал в пересечении с одним и тем же отрезком имеет ровно одну точку пересечения и в то же время не меньше двух точек пересечения. Это противоречие.

Не отрезок имеет одновременно одну и не одну точку пересечения, а разные $F_n$ из разных представлений отрезка.

-- 28.12.2025, 15:40 --

warlock66613 в сообщении #1713473 писал(а):

cxzbsdhwert в сообщении #1713468 писал(а):

Поэтому

Нет, никаких "поэтому". Мы конкретно доказываем, что некоторый отрезок и некоторый интервал имеют ровно одну точку пересечения. Это утверждение о самом отрезке, никаких "представлений" и "элементов представлений" в нём не упоминается.

А вот это уже не так. Вы ранее заявили, что я не правильно воспроизвёл доказательство, и привели дословно правильное:

warlock66613 в сообщении #1713451 писал(а):

Вот обсуждаемое доказательство:

skobar в сообщении #1713372 писал(а):

1.Пусть отрезок $[a,b], a<b$ счётен, тогда $[a,b]=\cup_{n} \{x_n\}$, то есть отрезок представлен в виде объединения счетного числа одноточечных множеств. Напомним, что всякое одноточечное множество на вещественной прямой замкнуто.
2. По следствию из теоремы Бэра найдется интервал, пересекающийся с нашим отрезком $[a,b]$ такой, что его пересечение с отрезком целиком лежит в каком-то одноточечном множестве $\{x_n\}$
3. Но, как правильно говорит лектор, "пересечение интервала с отрезком состоит уж по крайней мере из двух точек" (если оно непусто, а оно непусто)
4. Получили, что какое-то одноточечное множество $\{x_n\}$ содержит в качестве подмножества множество, в котором по крайне мере две точки (на самом деле, конечно, бесконечно много точек). Противоречие.

Как видите про представления здесь речь более чем идёт. Иронично, что в моей "неправильной", по Вашему мнению, формулировке слово "представление" не содержится.
Дело тем не мене, конечно не в слове "представление", оно вполне корректно, а в смысле которое оно отображает. Описал всё подробно выше.

[warlock66613]

cxzbsdhwert в сообщении #1713474 писал(а):

Не отрезок имеет одновременно одну и не одну точку пересечения, а разные $F_n$ из разных представлений отрезка.

Нет, именно отрезок:

skobar в сообщении #1713372 писал(а):

интервал, пересекающийся с нашим отрезком $[a,b]$ такой, что его пересечение с отрезком

-- 28.12.2025, 17:48 --

cxzbsdhwert в сообщении #1713474 писал(а):

А вот это снова не правильно.

Это правильно. Два множества равны (это синоним слома "является"), если содержат одинаковые элементы. Множество $\{1,2\}\cup\{3,4\}$ является объединением четырёх одноэлементных множеств, поскольку содержит те же четыре элемента, что и это самое объединение. И хоть как вы его записывайте, оно всё равно будет тем же самым множеством и потому будет являться объединением одноэлементных множеств.

[cxzbsdhwert]

warlock66613 в сообщении #1713456 писал(а):

Один и тот же интервал в пересечении с одним и тем же отрезком имеет ровно одну точку пересечения и в то же время не меньше двух точек пересечения. Это противоречие.

Предъявите пожалуйста из Ваших следствий один и тот же отрезок и тот же интервал, такие что интервал одновременно одну и не одну точку пересечения с одним отрезком имеет.
Не сможете. И это вообще с доказательством несчётности отрезка не связано.

Вы перепутали отрезок $F$ и объединения $F_n$, которые ему равны. Один и тот же отрезок с одним и тем же интервалом имеет одно и то же число точек пересечения. Разное число точек пересечения с одним и тем же интервалом имеют разные $F_n$, из разных наборов $\{F_1, F_2, ...\}, \{F^{`}_1,F^{`}_2,...\}, ...$, объединения каждого из которых равно одному и тому же $F$.

Обращаю внимание, что данное противоречие в Вашем рассуждении я показал без использования слов "представления", которое Вам не понравилось.

[warlock66613]

cxzbsdhwert в сообщении #1713477 писал(а):

Предъявите пожалуйста из Ваших следствий один и тот же отрезок и тот же интервал, такие что интервал одновременно одну и не одну точку пересечения с одним отрезком имеет.

Пусть существует отрезок, который является не более чем счётным множеством. $\leftarrow$ Вот я предъявляю вам отрезок.

Тогда этот отрезок можно представить в виде объединения одноэлементных множеств: $\{x_1\} \cup \{x_2\} \cup \{x_3\} \cup \ldots$. Тогда по теореме Бэра существует пересекающийся с отрезком интервал, пересечение которого с этим отрезком содержится ($\subseteq$) в некотором $\{x_i\}$. $\leftarrow$ Вот я предъявляю интервал.

Раз пересечение отрезка и интервала содержится в одноэлементном множестве, то оно состоит ровно из одной точки. $\leftarrow$ Вот я доказал что пересечение отрезка и интервала состоит из одной точки.

В то же время, верно, что любой отрезок и любой интервал, если только пересекаются, то пересекаются как минимум в двух точках. Значит и наши конкретные отрезок и интервал пересекаются минимум в двух точках. $\leftarrow$ Вот я доказал, что пересечение всё того же отрезка и всё того же интервала состоит минимум из двух точек.

Получаем противоречие.

[cxzbsdhwert]

warlock66613 в сообщении #1713478 писал(а):

cxzbsdhwert в сообщении #1713477 писал(а):

Предъявите пожалуйста из Ваших следствий один и тот же отрезок и тот же интервал, такие что интервал одновременно одну и не одну точку пересечения с одним отрезком имеет.

Пусть существует отрезок, который является не более чем счётным множеством. <- Вот я предъявляю вам отрезок. Тогда его можно представить в виде объединения одноэлементных множеств: $\{x_1\} \cup \{x_2\} \cup \{x_3\} \cup \ldots$. Тогда по теореме Бэра существует пересекающийся с отрезком интервал, пересечение которого с этим отрезком содержится ($\subseteq$) в некотором $\{x_i\}$. <- Вот я предъявляю интервал. Раз пересечение отрезка и интервала содержится в одноэлементном множестве, то оно состоит ровно из одной точки. <- Вот я доказал что пересечение отрезка и интервала состоит из одной точки. В то же время, верно, что любой отрезок и любой интервал, если только пересекаются, то пересекаются как минимум в двух точках. Значит инаши конкретные отрезок и интервал пересекаются минимум в двух точках. <- Вот я доказал, что пересечение всё того же отрезка и всё того же интервала состоит минимум из двух точек. Получаем противоречие.

А вот это то, о чём я писал с самого начала...

А на каком основании, доказывая от противного, то бишь полагая отрезок не более чем счётным, Вы и Лектор задействуете утверждение о том что пересечение должно быть больше чем из двух точек?
Мы можем предъявить нбчс множество, даже в виде объединения одноточечных если хотите, и интервал, так, чтобы его пересечение с множеством состояло из одной точки. Ну Вы собственно это и сделали.
Аксиомы полноты всякие, тут же уже не применишь.

Понятно, что по определению отрезка $[a,b]$ это упорядоченное множество всех вещественных чисел больших либо равных $a$ и меньше либо равных $b$, ну и исходя из полноты $\mathbb R$ в любой окрестности например $a$ будет точка из отрезка, соответственно подобрать такой интервал, чтобы он "захватил" только $a$ не получится.
Но мы же полагая от обратного наверное всё-таки по другому смотрим на природу отрезка.

[warlock66613]

cxzbsdhwert в сообщении #1713479 писал(а):

А на каком основании, доказывая от противного, то бишь полагая отрезок не более чем счётным, Вы и Лектор задействуете утверждение о том что пересечение должно быть больше чем из двух точек?

Это утверждение верно для любых пар отрезок/интервал. Значит оно верно и для не более чем счётного отрезка и рассматриваемого интервала.

-- 28.12.2025, 18:22 --

cxzbsdhwert в сообщении #1713479 писал(а):

Аксиомы полноты всякие, тут же уже не применишь.

Применишь конечно.

[cxzbsdhwert]

warlock66613 в сообщении #1713480 писал(а):

Это утверждение верно для любых пар отрезок/интервал

Конечно, если они оба несчётны. Ну почти. Это наверное верно и для рационального интервала.