Э, решайте-ка за себя, товарищ революционер.
Аа, за меня уже решили давно Кострикин с Маниным и Дьедонне, господин реакционер. Они на моей стороне, не нашлось места в их учебниках вычислениям определителей разложением по строке.
Просто берем учебники по линейной алгебре (Воеводин, Тыртышников, Беклемишев) и смотрим, как там излагаются эти вопросы. Авторы этих учебников известные люди именно в прикладной линейной алгебре. И после этого соотносим свои революционные идеи с реальностью.
"Известные люди именно в прикладной линейной алгебре" прекрасно понимали бессмысленность вычисления определителя разложением по строке с прикладной точки зрения, но надо принимать во внимание, что в советское время учебники, особенно для младших курсов, должны были строго следовать программе, утвержденной министерством образования СССР. Поэтому и появлялись такие темы в учебниках, написанных прикладниками. Мех-мату позволялись вольности, отдельно взятым личностям, в результате появлялись такие инновационные учебники, как Кострикина-Манина, Зорича, Арнольда и др.
Как уже написали, из правила Крамера следует весьма полезное утверждение: Если

удовлетворяет системе

, где
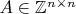
,
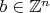
, то
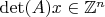
. И явная формула через определители бывает полезна для оценки величины решения.
А из явной формулы для обратной матрицы следует важный факт, что целочисленная квадратная матрица имеет целочисленную обратную тогда и только тогда, когда её определитель равен

.
Записываем её решения, как решения некоей системы линейных уравнений, показываем (через разложение), что определитель, стоящий в знаменателе, может быть один или минус один, а в числителе определитель целочисленной матрицы (соответственно, целое число), и понимаем, что целочисленность у нас получается без дополнительных усилий.
Теория чисел, целочисленное программирование, что-то дискретное, и если еще матрицы разреженные (содержат много нулей), то да, возможно будет какая-то польза от формулы Крамера. В теории графов, наверняка, может быть подобная ситуация.
Однако, вопрос стоял надо ли знать это всем. В вышеуказанных учебниках нет этих тем (у Дьедонне, правда, есть формула Крамера). Аспирант или специалист, работающие в этих областях, могут освоить всю эту технику за 1-2 дня, при условии, что до того ничего не знали про это.
А чтобы понять, что собственных значений n, надо воспользоваться правилом Крамера и расписать определитель.
При приведении матрицы к Жорданновой форме это получается даром, и даже больше.
Заморочно. Пара лишних действий.
В уме легче посчитать (на лекции, или читая учебник) определитель, чем выражать, а потом подставлять.
В уме прикинул, выписать определители, перемножить диагонали, вычесть одно из другого, заменить два раза столбец определителя, повторить, разделить определители на определитель.
Итого у меня получилось 12 флопсов, предел возможности человеческой оперативной памяти. В тоже время, решая подстановкой, тратим только 6 флопсов, т.е. в 2 раза меньше.