eprosСпасибо.
Хочу удостовериться, что все правильно понял.
Дело не в функциях.

означает то же самое, что

. Просто если Вы используете символы из разных наборов, читатель может оказаться в недоумении по поводу того, что Вы хотели этим сказать. Это могло бы быть оправданным, если бы Вы хотели этим подчеркнуть, что не хотите использовать символ из алфавита теории, поскольку высказываете метатеоретическое утверждение.
Вроде понятно. Символы

и

изпользуются для одного и того же, поэтому формально смешивать (в одном и том же изложении) нельзя, в алфавите вычисления высказываний для этого только один символ.
Далее буду использовать только

.
Выражение

корректно и может быть истинным или ложным в зависимости от значений пропозициональных переменных.
Если хотите сказать о равносильности, просто напишите

. Это утверждение - тавтология, что и означает равносильность его левой и правой частей.
Ок. Отдельного значка аналогичному

для обозначения тождественности формул не существует.
На этой роли достаточно использовать

(см. ниже).
Знак

это двуместный булевой оператор (предикат), полностью аналогичный

,

, с таблицы истинности

если оба булевых аргумента одинаковы, и

если разные.
Его, точно как и

,

можно вставлять между любыми формулами/переменными/константами и получим новую синтактически правильную формулу (чье значение будет вычисляться в зависимости от значений переменных):




Эквивалентность (тождественность) двух формул можно выразить через новую формулу, просто вставив

между ними, как здесь:

При такой "вставки"

между двух формул, в общем случае значение новой формулы будет зависеть от значений переменных. Но может получиться и так, что новая формула окажется константой, и ее значение не зависит от значения переменных (

- "тавтология",

- "противоречие").
Первый случай - тавтология (новая формула равна тождественно

вне зависимости от значений переменных) - это и значит что формулы по обоих сторон тождественны, потому и отдельный значок (аналогичный

) не нужен.
Все верно?
Контрольный вопрос, такая формула (с множеством

) синтактически правильна?:

(я полагаю, да).
А это вообще синтаксически некорректно. Равенство ставится между термами, а не между формулами. В исчислении высказываний равенства вообще нет.
В вычислении высказываний нет значка равенства (его "роль" в каком-то "смысле" выполняется

, если этого символа у нас есть рядом с

,

).
Понятия "терма" тоже нет (по меньшей мере
здесь такое понятие отсутствует).
Т.е. записи типа

,

частью языка не являются (зато мы можем строить формулы через

:

,

)
Теперь про

и

.
Насколько я понимаю, все что сказано выше про роль

и

, полностью аналогично относится и к

и

.
Только разумеется, таблица истинности

соответственно другая.
Все верно?
-- 03.03.2024, 18:49 --и, соответственно, четыре обозначения:

,

,

,
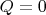
. Мои обозначения проще:

,

,

,

, -- и с ними проще работать, например, если надо записать конъюнкцию первого и третьего фактов, то у вас (пишу "вас" с маленькой буквы, потому что отвечаю сразу двоим) будет:

, -- а у меня:

.
Нет.
Коньюнкцию ваших двух фактов достаточно записать как

.
Она будет принимать значение

если обe утверждения

и

принимают значения

, и иметь значение

во всех остальных случаев значений

и

.
"Малые буковки"

совершенно ненужны! Нужна только одна пара буковок ("переменных") -на каждого из двух утверждений - и каждая из этих буковок ("переменных") может принимать значения

или

в зависимости верности или нет соответного утверждения.
Если нужно записать "верность" утверждения

- можно писать только

- значение этого выражения будет

если

верно, и

если неверно.
Точно также как пишем просто "x делится на 2" (что может быть как истиной, так и ложью), а не избыточно "то, что х делится на 2 - верно" (что будет истиной или ложью в тех же самых случаев).
Писать

или

конечно тоже можно, но избыточно. (запись

как выяснилось строго говоря некоректна, знак

не часть алфавита вычисления высказываний).