Решим уравнение в натуральных числах

Перенесём всё в одну сторону и сгруппируем

Отсюда сразу видно, что

поскольку
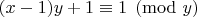
. А значит, два взаимно простых множителя

и

дают четвёртую степень

, то есть оба они сами — четвёртые степени:


для некоторых натуральных

и

. Тогда из
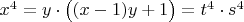
получаем

Кроме того,
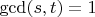
.
Подставляя

и

во второе равенство, получаем ключевое диофантово уравнение
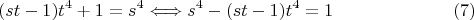
1) Случай

. Тогда из

имеем

. Отсюда

и

.
2) Случай

. Из

получаем

Отсюда сразу следует неравенство
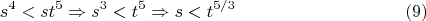
Кроме того, так как

, то
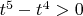
, и потому
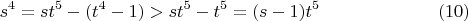
а значит при


Итак, при

и

имеем «зажатость»

Далее разберём чётность

.
2a)

нечётно (
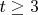
). Тогда

нечётно и из разложения
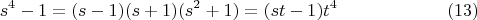
видно, что нечётный множитель

целиком сидит в одном из взаимно простых нечётных множителей
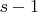
,

,
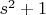
.
Но из (9) имеем

(так как
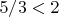
), следовательно


а из (9) также следует

(поскольку
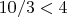
), то есть

Значит, ни один из трёх множителей
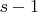
,

,
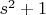
не может быть кратен

— противоречие. Следовательно, нечёткий

невозможен, и при

остаётся только чётный

.
2b)

чётно. Пусть
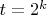
с

. Тогда из

получаем

Так как

чётный, то

чётно и

нечётно; отсюда

обязан быть нечётным (иначе левая часть была бы чётной). Для нечётного

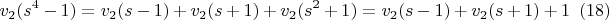
причём ровно один из
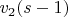
и
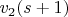
равен

, а другой

.
Поскольку
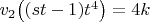
и

нечётно, имеем

Значит,

то есть «большая» из двух оценок
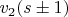
равна
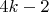
.
Минимально это возможно при
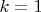
, когда
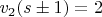
; при

пришлось бы иметь

(то есть
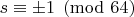
).
Теперь посмотрим на само уравнение при фиксированном

:
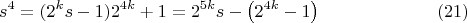
Левая часть растёт как

, правая — линейно по

.
Из (12) для
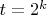
(и

) имеем
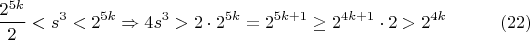
Следовательно, разность соседних четвёртых степеней

строго больше длины «коридора» по правой части (21), равной

. Поэтому при

равенство (21) не может выполниться ни при каком целочисленном

: между двумя соседними четвёртыми степенями интервал слишком широк, чтобы точное линейное значение

попало в

. Отсюда остаётся единственный чётный случай —
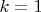
, то есть

.
При

уравнение (7) даёт

Лёгкая проверка показывает, что единственный натуральный корень —

(для
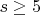
левая часть уже положительна и строго возрастает). Тогда
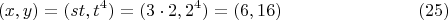
Итак, единственные решения в натуральных числах:

