Проверка способности LLM решать математические задачи

[Klein]

Wolfram Mathematica, Matlab, Python/sympy не смогли вычислить интеграл. Пишут Maple хорош с символическими вычислениями. Не проверял.

$\int \frac{(x^2-1)}{(x^2+1)\sqrt{x^4+1}}\,dx$


ChatGPT успешно справился. Интересно каким образом ? Если не через Питон/sympy.

[nnosipov]

Klein
Если вычислять этот интеграл как неопределенный

int((x^2-1)/(x^2+1)/sqrt(x^4+1),x);

то Maple выдает ответ в спец. функциях. Но если набрать

int((x^2-1)/(x^2+1)/sqrt(x^4+1),x=a..b);

то получается коротенький ответ в элементарных функциях, откуда легко извлечь первообразную:

$$\frac{1}{\sqrt{2}}\arctg{\frac{\sqrt{x^4+1}}{\sqrt{2}x}}.$$

Проверка дифференцированием показывает, что это правда.

-- Вт ноя 25, 2025 10:51:37 --

Klein в сообщении #1710551 писал(а):

ChatGPT успешно справился. Интересно каким образом ?

Просто натыкал правильную последовательность ходов. Попробуйте скормить ему что-нибудь типа

$$\int\sqrt{\pm 1+\sqrt{1+x^4}}\,dx$$

[Klein]

Установил Maple, и Maple посчитал

[nnosipov]

Klein
Не загружается картинка, не могу посмотреть.

[Klein]

nnosipov в сообщении #1710676 писал(а):

Klein
Не загружается картинка, не могу посмотреть.

https://i.imgur.com/RZ5ulSr.png

[nnosipov]

Вот теперь посмотрел, спасибо. Значит, стало лучше, я вычислял в Maple 2021.

[mihaild]

«Рабочее доказательство Задачи Тысячелетия - Гипотезы Римана» - Gemini 3 после двух подпинываний (изначально в PDF перепутало $p_m - 1$ и $p_{m - 1}$) сумело правильно найти ошибку.

(Ответ)

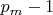
Even if we fix the typo by assuming the exponent is $p_m - 1$ (consistent with the context), the proof still fails.
While correcting the variable name fixes the transcription error in Equation (9), a fatal algebraic error occurs immediately after in the transition to Equation (10).
Here is the step-by-step mathematical reconstruction:

1. The Corrected Inequality (Eq 9)

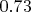
Fixing the typo in Equation (9) 1and using the established lower bound of $0.73$ from Corollary 2.12, the inequality becomes:

$$0.73 \cdot p_m^{\frac{1}{p_m-1}} < 1 + \frac{0.006788}{\log p_m}$$

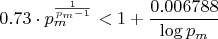
2. The Algebraic Error (Eq 10)

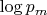
The author attempts to isolate $\log p_m$ to generate a contradiction. Let's perform the rearrangement carefully:
Subtract 1 from both sides:

$$0.73 \cdot p_m^{\frac{1}{p_m-1}} - 1 < \frac{0.006788}{\log p_m}$$

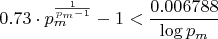
Analyze the Sign of the Left Side:
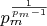
The term $p_m^{\frac{1}{p_m-1}}$ decreases towards 1 as $p_m$ increases. For $p_m \ge 8$, $p_m^{\frac{1}{p_m-1}} \approx 1$.
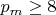
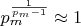
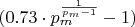
Consequently, the term $(0.73 \cdot p_m^{\frac{1}{p_m-1}} - 1)$ is negative (approximately $0.73(1) - 1 = -0.27$).
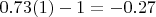
Isolate $\log p_m$:
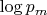
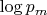
To isolate $\log p_m$, we must divide by the term $(0.73 \cdot p_m^{\frac{1}{p_m-1}} - 1)$.
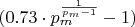
Crucially, when dividing an inequality by a negative number, the direction of the inequality must flip.
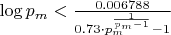
The Paper's Claim (Eq 10): $\log p_m < \frac{0.006788}{0.73 \cdot p_m^{\frac{1}{p_m-1}} - 1}$ 3


The Correct Algebra: $\log p_m > \frac{0.006788}{0.73 \cdot p_m^{\frac{1}{p_m-1}} - 1}$

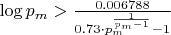
3. The Collapse of the Contradiction

The author's intended contradiction relies on Equation (10) being an upper bound ($\log p_m < X$).
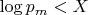
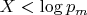
Lemma 2.3 gives the lower bound: $X < \log p_m$4.


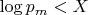
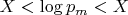
If Equation (10) were correct ($\log p_m < X$), we would have $X < \log p_m < X$, which is a contradiction.
However, because the sign flips, the corrected derivation yields:

$$\log p_m > X$$

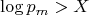
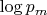
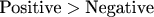
Since $X$ is a negative number (numerator positive / denominator negative) and $\log p_m$ is a positive number, this statement ($\text{Positive} > \text{Negative}$) is trivially true. It is consistent with Lemma 2.3 and does not produce a contradiction.
Conclusion: The proof relies on a sign error in elementary algebra. Correcting the typo in the exponent does not salvage the proof.
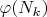
Next Step: Since the proof appears invalid, would you like me to identify if there are any known valid bounds for $\varphi(N_k)$ that are close to what the author was attempting to prove?

[MoonWatcher]

С Телеграм-канала Data Secrets:

ИИ-математик Aristotle доказал одну из нерешенных проблем из списка Эрдеша (но с оговоркой)

Если вы в первый раз слышите про Aristotle, рассказываем: это система от стартапа Harmonic, основанного в 2023 году. Ребята занимаются ИИ в математике, уже получили немало инвестиций, и продукт у них довольно интересный.

Он отличается тем, что генерирует не просто текст доказательства: вместо этого Aristotle пишет формальное доказательство в среде Lean, то есть сочетает в себе formal verification и informal reasoning + search.

Ну так вот. На днях создатели объявили о том, что модель решила проблему Эрдеша номер 124. Эта задача впервые была выдвинута в статье «Полные последовательности множеств целых степеней» в журнале Acta Arithmetica почти 30 лет назад и с тех пор считается открытой.

Aristotle же потратил на задачу 6 часов и решил ее абсолютно без участия человека. Потрясающе? Потрясающе.

Вот только оказалось, что версия задачи, которую решил Aristotle, отличается – это упрощенный вариант. Оригинальная формулировка была несколько другой и допускает увеличение степени только начиная с определенной, не включая единичную. В той формулировке задача остается нерешенной. И хотя результат действительно крутой, прорыва (сюрприз-сюрприз) снова не произошло.

Все это в который раз доказывает: да, какую-то новую математику модельки уже способны доказывать. Но это, что называется, «низко висящие плоды» – то есть довольно простые по меркам академии утверждения уровня среднего аспиранта или олимпиадника. До гипотезы Римана им еще как пешком до Китая.

-- 01.12.2025, 13:59 --

MoonWatcher в сообщении #1711319 писал(а):

До гипотезы Римана им еще как пешком до Китая

Интересно что по этому поводу думают в Китае...

[Rasool]

Ради интереса я задал бесплатной версии ChatGPT следующую вступительную задачку в ЗФТШ:

Цитата:

Можно ли разместить семь точек в пространстве так, чтобы любые три из них являлись вершинами равнобедренного треугольника?

Получил следующий неправильный ответ:

Цитата:

Короткий ответ: **Нельзя**. Максимальное число таких точек в евклидовом пространстве — **5**. Я приведу конструкцию для 5 и короткое доказательство невозможности 6 (и тем более 7).

**Конструкция для 5.** Возьмём правильный тетраэдр (4 вершины) и его центр (точка, равноудалённая от всех 4 вершин). Любая тройка вершин тетраэдра даёт равносторонний (=> равнобедренный) треугольник; любая тройка, содержащая центр и две вершины, даёт треугольник, у которого две стороны (от центра к вершинам) равны. Значит все треугольники из этих 5 точек — равнобедренные.

**Почему 6 точек невозможно (краткая схема доказательства).**

1. Пусть (S) — такое множество точек, предположим (|S|\ge6). Выберем пару (A,B\in S) на минимальном расстоянии (d=\overline{AB}) (т.е. никакие два точки не ближе друг к другу). Рассмотрим произвольную третью точку (X\in S\setminus{A,B}). По условию треугольник (ABX) равнобедренный, значит одна из равенств длин выполняется:

* (AX=d), или
* (BX=d), или
* (AX=BX).

Но (d) — минимальное расстояние, поэтому нельзя иметь (AX<d) или (BX<d); потому для каждой точки (X) действительно выполняется ровно одна из трёх перечисленных возможностей (в частности, если ни (AX) ни (BX) не равны (d), то обязательно (AX=BX)).

2. Разобьём остальные точки (вне (A,B)) на три классовые множества:

* (U) — точки на расстоянии (d) от (A) (включая (B)),
* (V) — точки на расстоянии (d) от (B) (включая (A)),
* (W) — точки, которые одинаково удалены от (A) и от (B) (т. е. лежат на перпендикулярной биссектрисе/многообразии середины отрезка (AB)).

Из пункта 1 видно, что каждую точку (кроме (A,B)) приходится относить в один из этих трёх классов.

3. Теперь основные ограничения:

* Точки из (U) и (V) не могут быть «сколь угодно многочисленными»: если в (U) есть хотя бы две точки (C,D) (обе на расстоянии (d) от (A)), то треугольник (BCD) (где (B) — другая вершина, с (\overline{AB}=d)) должен быть равнобедренным, что накладывает сильные симметрии на расположение таких точек. Аналогично для (V).
* Точки из (W) лежат на перпендикулярной биссектрисе отрезка (AB) (в трёхмерном пространстве — на соответствующей плоскости/окружности при фиксированных расстояниях). Для любых трёх точек из (W) треугольник между ними тоже должен быть равнобедренным, и это резко ограничивает возможное расположение: на одном круге/плоскости нельзя иметь больше трёх взаимоисключающих точек так, чтобы все треугольники между ними были равнобедренными (в простейшем разборе: если на окружности взять четыре различные точки, треугольник, составленный из трёх некоторым образом выбранных, обычно не будет равнобедренным; чтобы все треугольники на них были равнобедренными, точки должны вести себя как вершины правильного многоугольника малого размера — а это даёт очень малое число точек).

4. Из детального рассмотрения случаев (сколько точек может лежать в (U,V,W) одновременно и как они взаимодействуют) выходит, что помимо самих (A,B) суммарное число других точек не может превышать 3. Итого максимум (|S|=2+3=5).

(Другими словами: взяв пару на минимальном расстоянии, все остальные точки либо лежат на одном из двух шаров радиуса (d) с центрами в этих двух точках, либо на перпендикулярной биссектрисе; совместное требование «каждая тройка даёт равнобедренный треугольник» даёт противоречия при попытке иметь более трёх дополнительных точек.)

Если хотите, могу развернуть этот набросок в полностью строгий шаг-за-шаг доказательный вариант (с геометрическими выкладками и рассмотрением всех возможных конфигураций (U,V,W)), или показать другие конструкции максимального множества из 5 точек. Хотите — распишу детально.

[rockclimber]

Я спросил у платной версии 5.1. Она доказала, что на плоскости можно разместить 6 точек таким образом, а потом методом от противного доказала, что 7 точка уже не влезает, и многозначительно заключила, что "7 точек с требуемым свойством не существует ни на плоскости, ни в пространстве.".

[mihaild]

Gemini 3 Pro писал(а):

Да, разместить семь точек в пространстве так, чтобы любые три из них являлись вершинами равнобедренного треугольника, можно.

В евклидовом пространстве $\mathbb{R}^3$ максимальное количество точек, обладающих свойством, что любые три из них образуют равнобедренный треугольник, равно 8. Следовательно, конфигурация из 7 точек также существует.

Формальное доказательство (Конструкция)

Существование доказывается предъявлением конкретной конфигурации точек. Рассмотрим множество точек $S \subset \mathbb{R}^3$, состоящее из вершин правильного пятиугольника, его центра и точки, расположенной на перпендикуляре к плоскости пятиугольника, проходящем через центр.

Пусть $R > 0$. Определим координаты семи точек следующим образом:

1. Центр:
   
   $$P_0 = (0, 0, 0)$$
   
   
2. Вершины правильного пятиугольника в плоскости $z=0$ (радиус описанной окружности $R$):
   
   $$P_k = \left( R \cos \frac{2\pi k}{5}, R \sin \frac{2\pi k}{5}, 0 \right), \quad \text{для } k = 1, \dots, 5$$
   
   
3. Вершина на оси $z$ (на высоте $h=R$):
   
   $$P_6 = (0, 0, R)$$

Проверка условия:
Любая тройка точек из множества $\{P_0, \dots, P_6\}$ образует равнобедренный треугольник. Рассмотрим возможные типы троек:

• Тройка $\{P_i, P_j, P_k\}$ (где $1 \le i,j,k \le 5$):
  Любые три вершины правильного пятиугольника образуют равнобедренный треугольник в силу симметрии.
  
• Тройка $\{P_0, P_i, P_j\}$ (центр и две вершины пятиугольника):
  $|P_0 P_i| = |P_0 P_j| = R$. Треугольник равнобедренный.
  
• Тройка $\{P_6, P_0, P_i\}$ (вершина на оси, центр, вершина пятиугольника):
  $|P_6 P_0| = R$ и $|P_0 P_i| = R$. Треугольник равнобедренный (прямоугольный с катетами $R$).
  
• Тройка $\{P_6, P_i, P_j\}$ (вершина на оси и две вершины пятиугольника):
  В силу вращательной симметрии, расстояния от точки $P_6$ до любой вершины пятиугольника $P_k$ равны:
  
  $$|P_6 P_k| = \sqrt{R^2 + R^2} = R\sqrt{2}$$
  
  Следовательно, $|P_6 P_i| = |P_6 P_j| = R\sqrt{2}$. Треугольник равнобедренный.

Ссылка
Данный результат является частным случаем задачи об isosceles sets (равнобедренных множествах). Максимальная мощность такого множества в $\mathbb{R}^3$ была установлена Крофтом:

• Croft, H. T. (1962). "9-point and 7-point configurations in 3-space". Proceedings of the London Mathematical Society.

Для $\mathbb{R}^3$ верхняя грань равна 8 (добавляется точка $P_7 = (0,0,-R)$).

[nnosipov]

Цитата:

Таким образом, кажется, что мой первоначальный подход был ошибочным. В свете этого, возможно, решение использует более изощренные методы.

Я сдаюсь. Может, есть другой способ.

Это deepseek в очередной раз пытался доказать, что уравнение $x(y^3-2x^3)=y^2-1$ неразрешимо в натуральных числах. Первый раз наблюдаю, как он сдается. (Правда, я его полчаса мариновал, указывая на разные косяки в рассуждениях.)

[mihaild]

nnosipov
Посмотрите, пожалуйста. Я, по крайней мере, ошибок не нашел. Концептуальных точно не вижу, арифметических вроде тоже (и они уже давно у Pro модели встречаются редко).

(Gemini 3 Deep Think)

To find all solutions of the equation $x(y^3 - 2x^3) = y^2 - 1$ in natural numbers, we denote the set of natural numbers as $\mathbb{N}_0 = \{0, 1, 2, \dots\}$.
1. Analysis of Trivial Cases
Case 1: $x = 0$
Substituting $x = 0$ into the equation:

$$0 \cdot (y^3 - 0) = y^2 - 1 \implies 0 = y^2 - 1 \implies y^2 = 1$$

Since $y \ge 0$, we have $y = 1$.
Thus, $(0, 1)$ is a solution.
Case 2: $x = 1$
Substituting $x = 1$ into the equation:

$$1 \cdot (y^3 - 2) = y^2 - 1 \implies y^3 - y^2 - 1 = 0$$

For $y = 1$, $1 - 1 - 1 = -1 \neq 0$.
For $y \ge 2$, $y^3 - y^2 - 1 = y^2(y - 1) - 1 \ge 4(1) - 1 = 3 > 0$.
Thus, there are no solutions for $x = 1$.
2. Analysis for $x \ge 2$
We rearrange the original equation to isolate terms:

$$x y^3 - 2x^4 = y^2 - 1$$

$$x y^3 - y^2 = 2x^4 - 1$$

$$y^2(xy - 1) = 2x^4 - 1$$

Step A: Establishing Bounds
We determine the range of $y$ relative to $x$.
Lower Bound: Suppose $y \le x$.
Then $y^2(xy - 1) \le x^2(x^2 - 1) = x^4 - x^2$.
For $x \ge 2$, $x^4 - x^2 < 2x^4 - 1$ (equivalent to $x^4 + x^2 - 1 > 0$), so the LHS is strictly less than the RHS.
Thus, $y > x$.
Upper Bound: Suppose $y \ge 2x$.
Then $y^2(xy - 1) \ge (2x)^2(2x^2 - 1) = 4x^2(2x^2 - 1) = 8x^4 - 4x^2$.
For $x \ge 2$, $8x^4 - 4x^2 > 2x^4 - 1$ (equivalent to $6x^4 - 4x^2 + 1 > 0$), so the LHS is strictly greater than the RHS.
Thus, $y < 2x$.
So, any solution must satisfy $x < y < 2x$.
Step B: Divisibility and Modular Constraint
From the equation $y^2(xy - 1) = 2x^4 - 1$, we see that $xy - 1$ divides $2x^4 - 1$.

$$2x^4 - 1 \equiv 0 \pmod{xy - 1}$$

Consider the term $y^2 - 2x^2$. We multiply by $x^2$ to relate it to the known congruence:

$$x^2(y^2 - 2x^2) = (xy)^2 - 2x^4$$

Since $xy \equiv 1 \pmod{xy - 1}$:

$$x^2(y^2 - 2x^2) \equiv 1^2 - 2x^4 = 1 - 2x^4 \equiv -(2x^4 - 1) \equiv 0 \pmod{xy - 1}$$

Since $\gcd(x, xy - 1) = 1$, $x^2$ is invertible modulo $xy - 1$, allowing us to cancel it:

$$y^2 - 2x^2 \equiv 0 \pmod{xy - 1}$$

This implies that $y^2 - 2x^2 = k(xy - 1)$ for some integer $k$.
Step C: Determining the Value of $k$
We verify if $k$ can be non-zero by examining the possible values of the product $k(xy-1) = y^2 - 2x^2$.
Case $k \ge 1$: This implies $y^2 - 2x^2 \ge xy - 1$, or $y^2 - xy - 2x^2 + 1 \ge 0$.
Factoring the quadratic part: $(y - 2x)(y + x) + 1 \ge 0$.
Since $y < 2x$ and $y, x \ge 1$, we have $y - 2x \le -1$ and $y + x \ge 3$.
Thus, $(y - 2x)(y + x) \le -3$.
Adding 1 gives $\le -2$, which contradicts the condition $\ge 0$.
So, $k$ cannot be $\ge 1$.
Case $k \le -1$: This implies $y^2 - 2x^2 \le -(xy - 1)$, or $y^2 + xy - 2x^2 - 1 \le 0$.
Factoring the quadratic part: $(y + 2x)(y - x) - 1 \le 0$.
Since $y > x$, $y - x \ge 1$. Also $y + 2x \ge 3x \ge 6$.
Thus, $(y + 2x)(y - x) \ge 6$.
Subtracting 1 gives $\ge 5$, which contradicts the condition $\le 0$.
So, $k$ cannot be $\le -1$.
The only remaining possibility is $k = 0$.
Step D: Final Contradiction
If $k = 0$, then $y^2 - 2x^2 = 0$, which implies $y^2 = 2x^2$.
Rearranging gives $(y/x)^2 = 2$, or $y/x = \sqrt{2}$.
Since $\sqrt{2}$ is irrational, there are no integer solutions for $x, y \ge 1$.
Conclusion
The only solution in natural numbers (including zero) is $(x, y) = (0, 1)$. If natural numbers are defined strictly as positive integers ($\mathbb{Z}^+$), there are no solutions.
Answer:
The only solution is $(x, y) = (0, 1)$.

[nnosipov]

mihaild в сообщении #1711747 писал(а):

Концептуальных точно не вижу

Да, их нет, это главное (арифметика не так важна). Надо же, Gemini натыкал правильную последовательность логических ходов. А сможет ли он это повторить?

Вот это еще можно ему скормить: $xy^3+y^2-x^5-1=0$ (solve in positive integers).

[mihaild]

nnosipov в сообщении #1711775 писал(а):

Вот это еще можно ему скормить: $xy^3+y^2-x^5-1=0$

После подпинывания (с первой попытки оно использовало $\delta^2 \equiv 1 \pmod x \Rightarrow \delta \equiv \pm 1 \pmod x$, получилось вот так.

(Gemini 3 Deep Think)

To solve the equation in positive integers:

$$x y^3 + y^2 - x^5 - 1 = 0$$

we analyze the possible values for $x$.
Case 1: $x = 1$
Substituting $x=1$ into the given equation:

$$1 \cdot y^3 + y^2 - 1^5 - 1 = 0$$

$$y^3 + y^2 - 2 = 0$$

Let $f(y) = y^3 + y^2 - 2$. We check for positive integer roots:
For $y=1$, $f(1) = 1 + 1 - 2 = 0$. Thus, $(1, 1)$ is a solution.
For $y \ge 2$, $f(y)$ is strictly increasing, so $f(y) \ge 2^3 + 2^2 - 2 = 10 > 0$.
Therefore, the only solution for $x=1$ is $(1, 1)$.
Case 2: $x > 1$
Rewrite the equation as:

$$y^2(xy + 1) = x^5 + 1$$

Step 2a: Establish bounds for $y$
First, we show that $y > x$. Suppose for the sake of contradiction that $y \le x$. Then:

$$y^2(xy + 1) \le x^2(x \cdot x + 1) = x^2(x^2 + 1) = x^4 + x^2$$

We compare this to the right-hand side $x^5 + 1$. For $x \ge 2$:

$$(x^5 + 1) - (x^4 + x^2) = x^4(x - 1) - x^2 + 1$$

Since $x \ge 2$, $x^4(x - 1) \ge 16(1) = 16$ and $x^2 \ge 4$. Thus, the difference is positive, implying $x^5 + 1 > x^4 + x^2 \ge y^2(xy+1)$. This contradicts the equation. Hence, we must have $y > x$.
Next, we establish an upper bound. From $x y^3 < x y^3 + y^2 = x^5 + 1$, we have $x y^3 < x^5 + 1$.
Dividing by $x$, we get $y^3 < x^4 + \frac{1}{x}$. Since $y$ is an integer and $x > 1$, this implies $y^3 \le x^4$, or roughly $y \le x^{4/3}$.
Step 2b: Use divisibility properties
From the equation $y^2(xy + 1) = x^5 + 1$, we see that $xy + 1$ must divide $x^5 + 1$.
Now consider the expression $x^2(x^3 + y^2)$. We can rewrite it as:

$$x^5 + x^2y^2 = (x^5 + 1) + x^2y^2 - 1 = y^2(xy + 1) + (xy - 1)(xy + 1)$$

$$x^2(x^3 + y^2) = (xy + 1)(y^2 + xy - 1)$$

This shows that $xy + 1$ divides $x^2(x^3 + y^2)$.
Since $\gcd(xy + 1, x) = 1$ (and thus $\gcd(xy + 1, x^2) = 1$), it must be that $xy + 1$ divides $x^3 + y^2$.
Let $m$ be the integer quotient:

$$m = \frac{x^3 + y^2}{xy + 1}$$

Since $x, y > 0$, $m$ is a positive integer.
We can determine $m$ modulo $x$. From the definition of $m$, we have $m(xy + 1) = x^3 + y^2$, which implies:

$$m(1) \equiv y^2 \pmod x$$

From the original equation $y^2(xy + 1) = x^5 + 1$, we have:

$$y^2(1) \equiv 1 \pmod x \implies y^2 \equiv 1 \pmod x$$

Combining these, we get $m \equiv 1 \pmod x$.
Step 2c: Bound $m$ to find a contradiction
We found $m = \frac{x^3 + y^2}{xy + 1}$. Since $y > x$, the denominator $xy + 1 > x^2$.
Thus, $m < \frac{x^3 + y^2}{x^2} = x + \frac{y^2}{x^2}$.
Using the bound $y \le x^{4/3}$ derived earlier ($y^3 \le x^4$):
$\frac{y^2}{x^2} \le \frac{(x^{4/3})^2}{x^2} = \frac{x^{8/3}}{x^2} = x^{2/3}$.
For $x \ge 2$, $x^{2/3} < x$. Thus $m < 2x$.
Since $m \equiv 1 \pmod x$, the possible values for $m$ are $1$ or $x + 1$.
Actually, for large $x$, $m$ is much smaller than $x$. Let's check if $m < x$.
Assume $m \ge x$. Then $\frac{x^3 + y^2}{xy + 1} \ge x \implies x^3 + y^2 \ge x^2y + x \implies y^2 - x^2y + x^3 - x \ge 0$.
The roots of the quadratic $P(y) = y^2 - x^2y + x^3 - x$ are approximately $x$ and $x^2$. Since $x < y < x^2$ (from $y > x$ and $y \approx x^{4/3}$), $P(y)$ should be negative.
Specifically, for $x \ge 2$, we have $y > x$. Also $y^3 \le x^4 \implies y \le x \cdot x^{1/3}$.
Since $x^{1/3} < x - 1$ is not always true for small $x$, we check the case $x=2$ separately.
For $x=2$: $y > 2$ and $y \le 2^{4/3} \approx 2.51$. No integer $y$ exists.
For $x \ge 3$: $y^2 - x^2y + x^3 - x < 0$ holds for $y \approx x^{4/3}$. Thus $m < x$.
Since $m < x$ and $m \equiv 1 \pmod x$, the only possible value is $m = 1$.
Substitute $m = 1$ into the relation $x^3 + y^2 = m(xy + 1)$:

$$x^3 + y^2 = xy + 1$$

$$y^2 - xy = 1 - x^3$$

$$y(y - x) = -(x^3 - 1)$$

$$y(x - y) = x^3 - 1$$

Since $x > 1$, the right-hand side is positive ($x^3 - 1 > 0$).
Since $y > 0$, we must have $x - y > 0$, which implies $y < x$.
But in Step 2a, we proved $y > x$.
This is a contradiction. Thus, there are no solutions for $x > 1$.
Answer: The only solution in positive integers is (x,y)=(1,1).

Вроде более-менее правильно. В абзаце 2c как-то мутно, но вроде бы утверждения верные и должны допиливаться.

nnosipov в сообщении #1711775 писал(а):

Да, их нет, это главное (арифметика не так важна).

Тут от арифметики зависит верность концептуальной части. Если неравенства на самом деле немного другие, то решения на $k$ могли бы и быть.