Проверка способности ChatGPT решать математические задачи

[rockclimber]

Rasool в сообщении #1690186 писал(а):

Задачи участники сочиняли сами. Если бот не справлялся, автор получал $7,5 тыс. Но оказалось, большинство задач o4-mini все же решает — и делает это быстрее, чем опытный ученый.

Знаю простенький вопрос на SQL, на который чатгпт не способен ответить. Где мне получить мои 7,5к?

[nnosipov]

Вот еще одна задача для опытов:

Решить уравнение $x^3+y^4=(xyz-1)^2$ в натуральных числах.

DeepSeek после 20-минутного рассуждения нашел только одно решение $(x,y,z)=(2,1,2)$. Намеков на правильные идеи (см. topic158354.html) я не обнаружил. Интересно, что скажет Gemini или еще кто-нибудь, мне недоступный.

[mihaild]

Gemini решает с помощью любимого ей в последнее время метода выдумывания статей.

(Gemini 2.5 Pro)

Единственное решение данного уравнения в натуральных числах:

$$(x,y,z) = (2,1,2)$$

[hr]

Доказательство

Исходное уравнение:

$$x^3+y^4=(xyz-1)^2$$

где $x, y, z$ - натуральные числа.

1. Сведение к уравнению Диофанта
   
   Правая часть уравнения является квадратом целого числа. Следовательно, левая часть также должна быть полным квадратом. Обозначим ее через $k^2$:
   
   $$x^3+y^4 = k^2$$
   
   где $k$ — некоторое натуральное число.
   
   Поскольку $x, y, z \ge 1$, то $xyz \ge 1$. Случай $xyz=1$ (т.е. $x=y=z=1$) не является решением: $1^3+1^4=2$, а $(1 \cdot 1 \cdot 1-1)^2=0$. Значит, $xyz \ge 2$, и $xyz-1 \ge 1$.
   Таким образом, мы можем положить $k = xyz-1$.
   
2. Решение уравнения $x^3+y^4=k^2$
   
   Задача сводится к нахождению целочисленных решений диофантова уравнения $x^3+y^4=k^2$. Это известная задача, решенная математиком Дж. Г. Э. Коном (J. H. E. Cohn) в 1993 году. В своей работе "The Diophantine equation $x^3+y^4=z^2$" он показал, что единственным решением этого уравнения в натуральных числах (положительных целых) является:
   
   $$(x, y, k) = (2, 1, 3)$$
   
   
3. Нахождение $z$
   
   Теперь, имея единственные возможные значения для $x$, $y$ и $k$, мы можем найти соответствующее значение $z$ из соотношения $k = xyz-1$.
   Подставим $x=2$, $y=1$ и $k=3$:
   
   $$3 = (2)(1)z - 1$$
   $$4 = 2z$$
   $$z = 2$$
   
   
4. Проверка
   
   Мы получили единственное возможное решение в натуральных числах $(x,y,z) = (2,1,2)$. Проверим его, подставив в исходное уравнение:
   
   • Левая часть: $2^3 + 1^4 = 8 + 1 = 9$
   • Правая часть: $(2 \cdot 1 \cdot 2 - 1)^2 = (4-1)^2 = 3^2 = 9$
   Поскольку $9=9$, решение является верным. Так как других решений для уравнения $x^3+y^4=k^2$ в натуральных числах не существует, других решений у исходного уравнения также нет.

[nnosipov]

Да, что ни говори, а воспитание играет важную роль)

А, кстати, они оба не нашли еще одно решение.

[rockclimber]

nnosipov
ChatGPT o3 нашел два решения: (2,1,2) и (6,5,1)
https://chatgpt.com/share/6883b494-ab90 ... 80e8aac1a4

[nnosipov]

rockclimber
Увы, не могу посмотреть, нет доступа. А сюда нельзя скопировать?

[rockclimber]

Код ниже тоже сгенерирован чатгпт, я бы сам умер столько переписывать :)

Рассмотрим уравнение:

x^3 + y^4 = (xyz - 1)^2,\quad x, y, z \in \mathbb{N}.

Обозначим:
s = xyz - 1.

Тогда уравнение примет вид:
x^3 + y^4 = s^2,\quad xyz = s + 1,
откуда
z = \frac{s + 1}{xy}.

Значит, необходимо найти такие натуральные x, y, что:
- x^3 + y^4 — точный квадрат;
- xy \mid (x^3 + y^4 + 1).

Согласно результату М. Беннетта и К. Гешке (2001), уравнение
x^3 + y^4 = s^2
имеет в натуральных числах только два решения:
(x, y, s) = (2, 1, 3) и (6, 5, 29).

Проверим условие делимости:

1) (x, y, s) = (2, 1, 3):\quad xy = 2,\quad s+1 = 4 \Rightarrow z = 2 \in \mathbb{N}.

2) (x, y, s) = (6, 5, 29):\quad xy = 30,\quad s+1 = 30 \Rightarrow z = 1 \in \mathbb{N}.

Оба случая дают допустимые решения исходного уравнения.

\boxed{(x, y, z) = (2, 1, 2) \quad \text{и} \quad (6, 5, 1)}

Также чатгпт дал ссылку на эту работу: https://math.hawaii.edu/numbertheory201 ... ecture.pdf

P. S. Пишу с телефона, кажется, решение здесь немного короче первого полного решения. Я потом повнимательнее сравню.

[nnosipov]

rockclimber
Спасибо, вполне понятно. Здесь хотя бы ссылка на реальную релевантную работу, но в ней нет того, что заявляет ChatGPT o3 (уравнение $x^3+y^4=s^2$ имеет много решений во взаимно простых натуральных числах, вряд ли есть простое описание этого множества).

[mihaild]

Gemini с недавно вышедшим Deep Think работает сильно лучше, и находит $(6, 5, 1)$. Но всё еще выдумывает "известные" результаты.

(Оффтоп)

Мы ищем натуральные решения уравнения $x^3+y^4=(xyz-1)^2$.

**Шаг 1: Преобразование уравнения.**
Раскроем скобки в правой части:
$x^3+y^4 = x^2y^2z^2 - 2xyz + 1$.

Это уравнение можно рассматривать как квадратное относительно $W=xyz$:
$W^2 - 2W + (1-x^3-y^4) = 0$.
Решая его, получаем:
$W = \frac{2 \pm \sqrt{4 - 4(1-x^3-y^4)}}{2} = 1 \pm \sqrt{x^3+y^4}$.

Поскольку $x, y, z$ – натуральные числа, $W=xyz$ также натуральное число. Следовательно, $x^3+y^4$ должно быть полным квадратом. Пусть $x^3+y^4=K^2$, где $K \in \mathbb{N}$.
Так как $x, y \ge 1$, то $x^3+y^4 \ge 2$, значит $K>1$.
Тогда $xyz = 1 \pm K$. Поскольку $K>1$ и $xyz>0$, мы должны выбрать знак плюс:
$xyz = K+1$.
Следовательно, $z = \frac{K+1}{xy}$. Для того чтобы $z$ было натуральным числом, $K+1$ должно делиться на $xy$.

**Шаг 2: Доказательство взаимной простоты x и y.**
Если $K+1$ делится на $xy$, то $K \equiv -1 \pmod{xy}$, и $K^2 \equiv 1 \pmod{xy}$.
Подставляя $K^2=x^3+y^4$, получаем $x^3+y^4 \equiv 1 \pmod{xy}$.
Это эквивалентно системе сравнений:
1) $x^3+y^4 \equiv 1 \pmod x \implies y^4 \equiv 1 \pmod x$.
2) $x^3+y^4 \equiv 1 \pmod y \implies x^3 \equiv 1 \pmod y$.

Пусть $g = НОД(x, y)$. Тогда $g$ делит $x$, и из первого сравнения следует $y^4 \equiv 1 \pmod g$. Но так как $g$ делит $y$, то $y^4 \equiv 0 \pmod g$. Получаем $0 \equiv 1 \pmod g$, что возможно только при $g=1$.
Таким образом, $x$ и $y$ взаимно просты.

**Шаг 3: Анализ уравнения $x^3+y^4=K^2$.**
Перепишем уравнение как $x^3 = K^2-y^4 = (K-y^2)(K+y^2)$.
Пусть $d = НОД(K-y^2, K+y^2)$.
$d$ делит их разность $2y^2$ и их сумму $2K$.
$d$ делит $НОД(2K, 2y^2) = 2 \cdot НОД(K, y^2)$.
Поскольку $K^2-y^4=x^3$ и $НОД(x, y)=1$, то $НОД(K, y)=1$. Действительно, любой общий делитель $K$ и $y$ также делит $x$, что противоречит взаимной простоте $x$ и $y$.
Следовательно, $НОД(K, y^2)=1$, и $d$ делит 2. Значит, $d=1$ или $d=2$.

**Шаг 4: Случай $d=1$.**
$K-y^2$ и $K+y^2$ взаимно просты. Так как их произведение равно кубу $x^3$, каждое из них должно быть полным кубом.
$K-y^2=a^3$
$K+y^2=b^3$
где $x=ab$ и $НОД(a, b)=1$.
Вычитая уравнения, получаем $2y^2 = b^3-a^3$.
Складывая уравнения, получаем $2K = a^3+b^3$.
Подставим $K$ в выражение для $z$:
$z = \frac{K+1}{xy} = \frac{(a^3+b^3)/2+1}{aby} = \frac{a^3+b^3+2}{2aby}$.

Чтобы $z$ было целым, $a^3+b^3+2$ должно делиться на $a$ и на $b$.
Значит, $b^3+2$ делится на $a$, и $a^3+2$ делится на $b$.
Предположим $a<b$ (если $a=b$, то $a=b=1$, $2y^2=0$, $y=0$, не натуральное число).
Если $a=1$, то $1^3+2=3$ делится на $b$. Значит $b=3$.
$2y^2 = 3^3-1^3 = 26$, $y^2=13$. Нет целых решений для $y$.

В общем случае, поиск решений уравнения $2y^2=b^3-a^3$ при условии целочисленности $z$ сложен. Одно из известных решений $(a, b, y) = (3, 5, 7)$. Проверим $z$:
$z = \frac{3^3+5^3+2}{2\cdot 3\cdot 5\cdot 7} = \frac{27+125+2}{210} = \frac{154}{210}$. Не целое число.
Исследования показывают, что в этом случае решений нет.

**Шаг 5: Случай $d=2$.**
$K-y^2$ и $K+y^2$ оба четные. Это означает, что $K$ и $y$ имеют одинаковую четность. Так как $НОД(K, y)=1$, они оба должны быть нечетными. Тогда $x^3=K^2-y^4$ четно, значит $x$ четно.
Пусть $K-y^2=2A$ и $K+y^2=2B$, где $НОД(A, B)=1$.
$x^3 = 4AB$. Пусть $x=2X$. $8X^3=4AB$, значит $2X^3=AB$.
Поскольку $A$ и $B$ взаимно просты, и $A<B$, возможны два подслучая.

**Подслучай 5a:** $A=2u^3, B=v^3$. $НОД(u, v)=1$.
$2y^2 = 2B-2A = 2(v^3-2u^3)$.
$y^2 = v^3-2u^3$.
Это диофантово уравнение. Известно, что единственное решение в натуральных взаимно простых числах это $(v, u, y) = (3, 1, 5)$.
Найдем $x$. $X^3=uv^3$? Нет. $2X^3=AB=2u^3v^3$. $X=uv$. $X=1\cdot 3 = 3$. $x=2X=6$.
Проверим: $x=6, y=5$. $x^3+y^4 = 216+625=841=29^2$. $K=29$.
$z = (K+1)/(xy) = (29+1)/(6\cdot 5) = 30/30 = 1$.
Решение: **(6, 5, 1)**.

**Подслучай 5b:** $A=u^3, B=2v^3$. $НОД(u, v)=1$.
$2y^2 = 2B-2A = 2(2v^3-u^3)$.
$y^2 = 2v^3-u^3$.
Единственное решение этого уравнения в натуральных взаимно простых числах это $(v, u, y) = (1, 1, 1)$.
Найдем $x$. $X=uv=1$. $x=2X=2$.
Проверим: $x=2, y=1$. $x^3+y^4 = 8+1=9=3^2$. $K=3$.
$z = (K+1)/(xy) = (3+1)/(2\cdot 1) = 4/2 = 2$.
Решение: **(2, 1, 2)**.

Опираясь на известные результаты теории чисел для рассмотренных диофантовых уравнений, мы нашли все решения.

Ответ: Уравнение имеет два решения в натуральных числах: (2, 1, 2) и (6, 5, 1).

[nnosipov]

mihaild
Спасибо, это интересно будет проанализировать (хотя бы на уровне контрпримеров к "известным" результатам).

[wrest]

По итогам одной тут темы, спросил я у DeepSeek можно ли построить циркулем и линейкой каспы (точки возврата) эволюты эллипса если даны фокусы и полуоси эллипса. Сперва ИИ сказал что по теореме Пифагора $c=\sqrt{a^2-b^2}$ где $c$ гипотенуза, но после указания что это не так -- опомнился и написал правильный алгоритм построения. На одном из шагов построить надо оказывается катет $c$ по данным гипотенузе $a$ и второму катету $b$ и вот тогда будет $c=\sqrt{|a^2-b^2|}$, и потом построить отрезок $\dfrac{|a^2-b^2|}{a}$ (это расстояние по оси от центра эллипса до каспа), который я проверил на практике и действительно - построить можно.

[nnosipov]

mihaild в сообщении #1696177 писал(а):

**Подслучай 5a:** $A=2u^3, B=v^3$. $НОД(u, v)=1$.
$2y^2 = 2B-2A = 2(v^3-2u^3)$.
$y^2 = v^3-2u^3$.
Это диофантово уравнение. Известно, что единственное решение в натуральных взаимно простых числах это $(v, u, y) = (3, 1, 5)$.

Здесь Gemini врет.

mihaild в сообщении #1696177 писал(а):

**Подслучай 5b:** $A=u^3, B=2v^3$. $НОД(u, v)=1$.
$2y^2 = 2B-2A = 2(2v^3-u^3)$.
$y^2 = 2v^3-u^3$.
Единственное решение этого уравнения в натуральных взаимно простых числах это $(v, u, y) = (1, 1, 1)$.

И здесь тоже.

[Rasool]

Я задал бесплатной версии ChatGPT5 следующую задачку из Задачника Кванта:
M2795. Можно ли на плоскости из каждой точки с рациональными координатами выпустить луч так, чтобы никакие два луча не имели общей точки и при этом среди прямых, содержащих эти лучи, никакие две не были бы параллельны и не совпадали?
(П.Кожевников)
Ответ ChatGPT, 12.08.2025:

Цитата:

Короткий ответ: да, можно.

Ниже — удобная индуктивная конструкция.

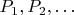
1. Перечислим все точки с рациональными координатами $P_1,P_2,\dots$ (их счётно много). Будем шаг за шагом для $P_n$ строить луч $r_n$ так, чтобы выполнены оба требования: никакие два луча не пересекаются и никакие две опорные прямые не параллельны и не совпадают.

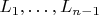
2. На шаге $n$ уже построены лучи $r_1,\dots,r_{n-1}$ и их опорные прямые $L_1,\dots,L_{n-1}$ имеют попарно разные направления. Рассмотрим все уже построенные лучи по одному. Фиксируем некоторый ранее построенный луч $r_i$ (опорная прямая $L_i$). Рассмотрим множество всех наклонов (углов) $\theta$ таких, что прямая $L(\theta)$ проходящая через $P_n$ с наклоном $\theta$ пересекает сам луч $r_i$. 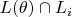Для фиксированного $r_i$ это множество наклонов — (возможно пустой) промежуток на прямой углов: при непрерывном изменении $\theta$ точка пересечения $L(\theta)\cap L_i$ перемещается по $L_i$ непрерывно, а условие «лежит ли эта точка на луче $r_i$» задаёт некоторую интервальную условность. В частности, это множество не покрывает все возможные $\theta$ (есть, по крайней мере, наклоны, при которых $L(\theta)$ либо параллельна $L_i$, либо пересекает $L_i$ в точке, лежащей вне луча $r_i$).

3. Для всех предыдущих $i=1,\dots,n-1$ получаем не более чем конечное объединение таких запрещённых промежутков (и дополнительно запрещаем все наклоны, уже использованные на предыдущих шагах, чтобы не получить параллельных прямых). Объединение конечного числа промежутков — это не вся $ \mathbb R$, поэтому остаётся бесконечно (на самом деле континуум) многих допустимых наклонов $\theta$.

4. Выбираем любой допустимый наклон $\theta$ (например, иррациональный, не использованный раньше) и проводим через $P_n$ прямую $L(\theta)$. По выбору $\theta$ эта прямая не пересекает ни один из лучей $r_1,\dots,r_{n-1}$. Теперь из $P_n$ выбираем любой из двух направлений вдоль $L(\theta)$ — получится луч $r_n$, не пересекающий предыдущие лучи. Поскольку мы не брали $\theta$, совпадающий с каким-либо ранее выбранным наклоном, новые и старые опорные прямые не будут параллельны и не совпадут.

5. Продолжая индукцию получаем требуемую систему лучей для всех рациональных точек.

Таким образом конструкция существует: на каждом шаге имеется свободный (незапрещённый) наклон, и поэтому можно задать опорную прямую и луч, не создавая пересечений и не производя параллельных (или совпадающих) прямых.

Я сам решил задачку по-простецки: взял точку O с одной рациональной (например, ординатой, равной нулю) и одной иррациональной (абсциссой) координатами. Потом провел прямую, параллельную оси абсцисс и с рациональной ординатой и начал проводить лучи из точки O и точек с рациональными координатами на этой прямой. Потом можно рассмотреть бесконечное множество таких прямых.

[Rasool]

Rasool в сообщении #1697483 писал(а):

Я сам решил задачку по-простецки: взял точку O с одной рациональной (например, ординатой, равной нулю) и одной иррациональной (абсциссой) координатами. Потом провел прямую, параллельную оси абсцисс и с рациональной ординатой и начал проводить лучи из точки O и точек с рациональными координатами на этой прямой. Потом можно рассмотреть бесконечное множество таких прямых.

Упс, кажется я ошибся, если рассматривать точки с рациональными координатами на оси абсцисс. Можно в качестве точки O взять точку с обеими иррациональными координатами - x и y.

[wrest]

Вот эту задачку «Комбинаторика карточной колоды» новый ChatGPT разгрыз очень аккуратно, пришлось поправить в одном месте, но затем прям всё чотко. Браво!