Gemini 2.5 Pro Thinking. Что-то находит, рассуждение имеет вид "где-то доказано что у чего-то [я не уверен, что имеющего какое-то отношение к делу] конечное число решений, значит два найденных решения - единственные".
We want to find all natural number (positive integer) solutions to the equation

.
Rearrange the equation:
We rearrange the terms:

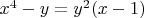
Analyze the case x = 1:
If

, the equation becomes

, so
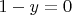
, which gives
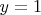
.
Thus,

is a solution.
Analyze the case x > 1:
We rewrite the equation as:
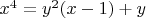
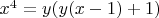
Let
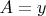
and
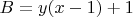
. Then
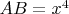
.
We calculate the greatest common divisor of A and B:

.
Since A and B are coprime and their product is a fourth power (

), both A and B must be fourth powers themselves.
Let

and

, where
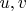
are positive integers and
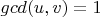
.
Then

and

.
Derive a new Diophantine equation:
We substitute these back into the relationship between A and B:
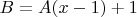
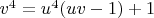
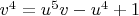
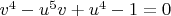
.
We look for positive integer solutions

to this equation. Since

, we are looking for solutions other than

. Thus we consider

.
Analyze the new equation for u ≥ 2:
We analyze the polynomial
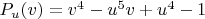
. We look for its positive integer roots.
We analyze the location of the positive roots. Let's evaluate
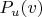
at
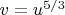
.
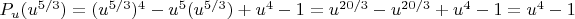
.
Since

,
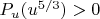
.
Let's evaluate
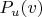
at
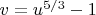
.

.
Expanding this expression yields:
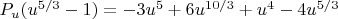
.
We analyze the sign of this expression. Let
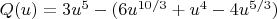
.
It can be shown that
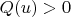
for all

. (This involves analyzing the function
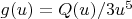
;

is increasing for

and
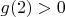
).
Thus,
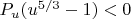
for all

.
Since
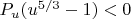
and
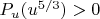
, the polynomial
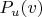
has a root

that lies strictly between

and

.
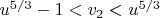
.
Implications for integer solutions:
The interval
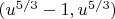
has length 1, so it contains at most one integer.
Case 1:

is a perfect cube. Let
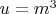
(

).
Then
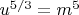
is an integer. The root

lies strictly between
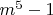
and

. Thus

cannot be an integer. There are no solutions in this case.
Case 2:

is not a perfect cube.

is irrational.
The unique integer in the interval is
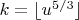
.
If there is an integer solution

, it must be

.
Let's check the first few values of

.
If

.

.

.
We check

:
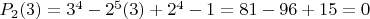
.
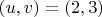
is a solution.

.
This gives
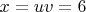
,
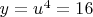
.
If

.
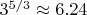
.

.

.
If
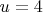
.
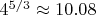
.

.
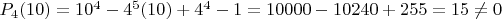
.
The Diophantine equation
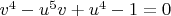
is known to have only finitely many integer solutions (by Siegel's theorem). The solutions

and

are the only positive integer solutions.
The solutions to the original equation in natural numbers are

and

.