Вы можете получить активную гравитационную массу, используя только аппарат ТО
Покажите, пожалуйста, как это делается (может быть я хоть так узнаю, что такое "активная гравитационная масса").
Раз вопрос задан, не делая слишком больших обобщений, предлагаю рассмотреть слабо гравитирующее газовое облако, состоящее из n частиц, с одинаковой массой покоя m, хаотично движущаяся со скоростью, имеющей абсолютное значение

в некоторой системе координат. Исследуется случай, когда искажения длины и времени, вызванные наличием Лоренц-фактора будут на порядок больше, чем искривление пространства-времени под действием гравитации. Предполагается, что в момент времени

расстояниями между частицами

можно пренебречь при определении гравитации, создаваемой этим облаком в рассматриваемой области, находящейся на удалении. Разрежение газа определяется условием

при скорости света

и

с гравитационной постоянной

и гравитационной массой облака

. Статистически облако может быть представлено в виде набора систем, состоящих из двух частиц А и В, которые движутся в противоположных направлениях.
Активная гравитационная масса этого этого облака оказывается

где

- полный эллиптический интеграл 2-го рода от

.
Как определяется активная гравитационная масса, то есть, притягивающая, та, что значится в выражении для ньютоновского гравитационного потенциала:
Слабо гравитирующее газовое облако состоит из одинаковых частиц с массой покоя

, хаотично движущаяся со скоростью, имеющей абсолютное значение

в некоторой системе координат

. Предполагается, что в момент времени

расстояниями

между частицами можно пренебречь при определении гравитации, создаваемой этим облаком в рассматриваемой области, находящейся на удалении. Разрежение газа определяется условием

(1)
при скорости света

и

с гравитационной постоянной

и гравитационной массой облака

. Статистически облако может быть представлено в виде набора систем, состоящих из двух частиц А и В, которые движутся в противоположных направлениях.
Рис. 1

Слабое гравитационное поле одной частицы приближенно описывается в связанных с ней координатах

линеаризованной изотропной метрикой Шварцшильда

(2)
при

и

.
Применение преобразований Лоренца к метрике ШварцшильдаУсловие (1) означает, что искажения длины и времени, вызванные наличием Лоренц-фактора

при

, будут на порядок больше, чем искривление пространства-времени под действием гравитации. Поэтому ее влияние на преобразования Лоренца

(3)
при

(4)
и

(5)
будет незначительно, и они могут быть применены к метрике (2). Преобразование координат при

(6) приносит

(7)
Система из двух телВ системах отсчета

,

, связанных с рассматриваемыми телами, Рис. 1, гравитация каждого из них в отдельности описывается в соответствующей системе метрикой (2). Перейдем от этих систем координат к

, используя преобразования Лоренца для скоростей (4), (5).
Если представить метрические коэффициенты в форме

(8)
где

соответствуют метрике Минковского, то при слабой гравитации [5] соотношение

(9)
выполняется для общего поля, созданного

подсистемами с метрическими коэффициентами

(10)
Суммируя коэффициенты метрик, получаемых после подстановок значений скоростей (4) и (5) в метрику (7), находим, что поле рассматриваемой гравитационной системы в окрестности

приближенно будет описываться метрикой

(11)
при

и

.
Получим ускорение материальной частицы в момент времени, когда она покоится в системе отсчета

. Из уравнений геодезических

для пространственных координат с индексами

, подставляя значения символов Кристоффеля

, находим

(12)
Это уравнение приносит координатные ускорения

(13)

(14)

(15)
без малых величин большего порядка.
Гравитационная масса облака газа Определим теперь среднюю гравитационную массу пары подобных частиц из облака газа, которое они образуют. Абсолютная величина ускорения частицы, находящейся на расстоянии

от тел, составит

(16)
или

(17)
Переходя к сферической системе координат с помощью преобразований



(18)
получим

(19)
Для каждой пары частиц из облака газа система координат выбирается так, что ось

параллельна линии их движения, и расстояние до них составляет

. В этом случае мы можем усреднить гравитационную массу одинаковых пар частиц, проявляющуюся в точке наблюдения, по углу

. При их массе покоя

она будет

(20)
Эта величина определяет гравитационную массу облака, состоящую из

частиц:

(21)
где

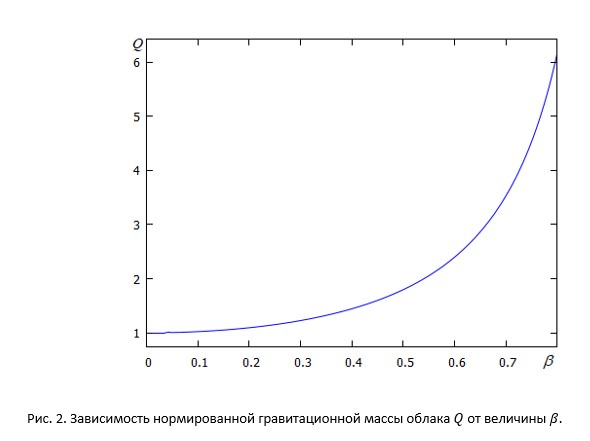
это полный эллиптический интеграл Лежандра 2-го рода. На рис. 2 показано, как отношение гравитационной массы облака к суммарной массе покоя его частиц

изменяется с увеличением скорости частиц.
|
! |
Доклад на конференции не становится авторитетным источником только потому, что оргкомитет его пропустил. Рецензирование на конференциях, даже если оно есть, на порядок слабее, чем в нормальных журналах. |
Все-таки IC-MSQUARE это конференция достаточно высокого уровня и статья проверялась редакторами самой конференции и издательством материалов конференций AIP, где она была опубликована. Да и по сложности этот материал не то, что доказательство восьмой проблемы Гильберта. Его может проверить любой, кто более менее шарит в ОТО, что неоднократно делалось и никто ошибки, влияющей на результат, не нашел.
Я правильно понимаю, что "активную гравитационную массу" Вы можете определить только для случая, когда гравитацией можно пренебречь? (и только для системы, которая развалится за короткое время?)
После этого хочется спросить, что Вы назваете "выводом по ТО"?
Есть понятие контрпримера. Если существует некая теория и в дополнение к ней задается некоторый постулат, в данном случае утверждение о том, что энергия и импульс материи как источники гравитационного поля составляют известный гидродинамический тензор, с помощью ковариантных преобразований которого можно получить его значение для движущейся материи, которое будет согласованным с остальной частью теории, то достаточно одного примера, который бы противоречил этому постулату, чтобы признать его ошибочным. В данном случае значение гравитационной массы облака движущихся частиц не может быть получено с помощью ковариантных преобразований тензора энергии-импульса покоящейся материи.
Попробую дать этому некоторое объяснение, хотя, возможно, оно и не вполне корректно. Применимость законов сохранения, задаваемых группой симметрии, определяется тем, какие измеряемые величины сопоставляются сохраняемым параметрам. Однако нельзя перевести материю из одной связанной с ней инерциальной системы отсчета в другую, не затратив энергию. Поэтому отдельно взятые энергия и импульс материи, как источник гравитации, не могут быть скомпонованы в ковариантный тензор энергии-импульса. Чтобы получить ковариантность, придется добавлять в преобразованный тензор какие-то дополнительные сущности, имеющие энергию и импульс. Но тогда получится, что начальный тензор должен быть дополнен, а в этом случае, преобразованный тензор снова изменится.