Итак, строим-строим.
 Дано:
Дано:Точка

-- откуда бросают груз, фокус параболы безопасности.
Прямая

- вертикаль (направлена по силе тяжести) и длина

- высота площадки с которой бросают.

расстояние между фокусом и директрисой параболы безопасности, соответственно красная прямая -- директриса парабола безопасности (считаем что она дана, но см. пункт 4 построения).
Построение.1. Строим перпендикуляр к оси параболы

в точке

-- это земля, зеленая прямая.
2. Проводим окружность радиусом равным
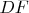
из центра

(синяя окружность).
3. Отмечаем точку пересечения

синей окружности с зеленой прямой. Это та точка, куда упадёт груз.
4. Строим точку

- это середина отрезка

и по совместительству вершина параболы безопасности (ну и

, т.е. можно считать что в задаче задана именно точка

, а не

, не принципиально).
5. Через точку

проводим перпендикуляр к оси параболы безопасности -- это директриса нашей траектории, фиолетовая прямая.
6. Строим серединный перпендикуляр к отрезку

и отмечаем точку его пересечения с директрисой траектории (фиолетовой прямой) как точку

7.

-- искомое направление, в котором бросать.
Альтернативное построение.Повторяем шаги 1-3.

4. Из точки

восстанавливаем перпендикуляр к земле (зеленой прямой) и отмечаем точку его пересечения

с директрисой параболы безопасности (красная прямая)
5. Направление

искомое, под которым бросать груз.
Тонким пунктиром и штрих-пунктиром справочно показаны парабола безопасности (огибающая всех траекторий из точки старта) и конкретная траектория соответственно.
-- 02.02.2021, 14:14 --Теперь запишем какое-нибудь решение исходя из построения.Например.
Треугольник

прямоугольный,

,

Обозначим, для простоты,

Тогда

По построению

Тангенс искомого угла, по определению тангенса,

так что

Подставляем

и получаем

ну или запишем через котангенс

Может синус или косинус покрасивей будут, не знаю.