11#: 2:17 4:13 6:23 8:89 10:139 12:1 14:113
13#: 2:17 4:19 6:23 8:89 10:139 12:199 14:113
17#: 2:29 4:19 6:23 8:89 10:139 12:199 14:113
19#: 2:29 4:37 6:23 8:89 10:139 12:199 14:113
23#: 2:29 4:37 6:31 8:89 10:139 12:199 14:113
29#: 2:41 4:37 6:31 8:89 10:139 12:199 14:113
31#: 2:41 4:37 6:47 8:89 10:139 12:199 14:113
37#: 2:41 4:43 6:47 8:89 10:139 12:199 14:113
41#: 2:59 4:43 6:47 8:89 10:139 12:199 14:113
43#: 2:59 4:67 6:47 8:89 10:139 12:199 14:113
47#: 2:59 4:67 6:53 8:89 10:139 12:199 14:113
53#: 2:59 4:67 6:61 8:89 10:139 12:199 14:113
59#: 2:71 4:67 6:61 8:89 10:139 12:199 14:113
61#: 2:71 4:67 6:73 8:89 10:139 12:199 14:113
67#: 2:71 4:79 6:73 8:89 10:139 12:199 14:113
71#: 2:101 4:79 6:73 8:89 10:139 12:199 14:113
73#: 2:101 4:79 6:83 8:89 10:139 12:199 14:113
79#: 2:101 4:97 6:83 8:89 10:139 12:199 14:113
83#: 2:101 4:97 6:131 8:89 10:139 12:199 14:113
89#: 2:101 4:97 6:131 8:359 10:139 12:199 14:113
97#: 2:101 4:103 6:131 8:359 10:139 12:199 14:113
101#: 2:107 4:103 6:131 8:359 10:139 12:199 14:113
103#: 2:107 4:109 6:131 8:359 10:139 12:199 14:113
107#: 2:137 4:109 6:131 8:359 10:139 12:199 14:113
109#: 2:137 4:127 6:131 8:359 10:139 12:199 14:113
113#: 2:137 4:127 6:131 8:359 10:139 12:199 14:293
127#: 2:137 4:163 6:131 8:359 10:139 12:199 14:293
131#: 2:137 4:163 6:151 8:359 10:139 12:199 14:293
137#: 2:149 4:163 6:151 8:359 10:139 12:199 14:293
139#: 2:149 4:163 6:151 8:359 10:181 12:199 14:293
149#: 2:179 4:163 6:151 8:359 10:181 12:199 14:293
151#: 2:179 4:163 6:157 8:359 10:181 12:199 14:293
157#: 2:179 4:163 6:167 8:359 10:181 12:199 14:293
163#: 2:179 4:193 6:167 8:359 10:181 12:199 14:293
167#: 2:179 4:193 6:173 8:359 10:181 12:199 14:293
173#: 2:179 4:193 6:233 8:359 10:181 12:199 14:293
179#: 2:191 4:193 6:233 8:359 10:181 12:199 14:293
181#: 2:191 4:193 6:233 8:359 10:241 12:199 14:293
191#: 2:197 4:193 6:233 8:359 10:241 12:199 14:293
193#: 2:197 4:223 6:233 8:359 10:241 12:199 14:293
197#: 2:227 4:223 6:233 8:359 10:241 12:199 14:293
199#: 2:227 4:223 6:233 8:359 10:241 12:211 14:293

 не должен превышать 2p, чтобы выполнялась гипотеза Лежандра
не должен превышать 2p, чтобы выполнялась гипотеза Лежандра максимальный интервал между соседними взаимно простыми с 197# числами
максимальный интервал между соседними взаимно простыми с 197# числами  . Число 197 по этой формуле - (
. Число 197 по этой формуле - ( ), соответствует разности квадратов
), соответствует разности квадратов  . Следовательно, мы можем утверждать, что между
. Следовательно, мы можем утверждать, что между  и
и  обязательно будет находиться как минимум одно простое число. И точно также это будет верно для всех остальных отрезков между соседними квадратами - между
обязательно будет находиться как минимум одно простое число. И точно также это будет верно для всех остальных отрезков между соседними квадратами - между  , между
, между  , ..., между
, ..., между  и
и  до
до  содержат простые числа.
содержат простые числа.  - не должно быть бесконечно много)
- не должно быть бесконечно много)
 .
.  и
и  и
и  , и следовательно между квадратами
, и следовательно между квадратами  и
и  обязательно будет находиться хотя бы одно простое число.
обязательно будет находиться хотя бы одно простое число. , и для
, и для  как раз выполняется.
как раз выполняется. .
. может взяться бОльшая разность, если ее не было на предыдущем праймориале?
может взяться бОльшая разность, если ее не было на предыдущем праймориале? может возникнуть в каком-то новом праймориале только на отрезке от
может возникнуть в каком-то новом праймориале только на отрезке от  до
до 
 попадет цепочка вычетов, кратных
попадет цепочка вычетов, кратных 
 .
. достигается при
достигается при  , т.е.
, т.е.  .
. . На границе 3ПСВ5
. На границе 3ПСВ5 и 4ПСВ5
и 4ПСВ5 :
:  . При следующем шаге решета Эратосфена и переходе к ПСВ7
. При следующем шаге решета Эратосфена и переходе к ПСВ7 .
. получается в первой ПСВ7
получается в первой ПСВ7 - в первой ПСВ11
- в первой ПСВ11 .
. в ПСВ не обязательно создавать ПСВ и искать в ней эту разность.
в ПСВ не обязательно создавать ПСВ и искать в ней эту разность.
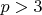 .
. не затрагивая вычетов 0 и
не затрагивая вычетов 0 и 
 , который и определяет ПСВ, в которой есть данная разность
, который и определяет ПСВ, в которой есть данная разность  . Берем группу вычетов с разностями (4,2,4,2...)
. Берем группу вычетов с разностями (4,2,4,2...)






 Следовательно, разности
Следовательно, разности 
 Но т.к. разность
Но т.к. разность  24
24  . Но обратите внимание, как при этом вкладывается интервал
. Но обратите внимание, как при этом вкладывается интервал  . Интервал
. Интервал  захватывает несколько ПСВ
захватывает несколько ПСВ , а интервал
, а интервал  , интервал
, интервал  и.т.д. Поэтому эти интервалы не могут находится на стыке ПСВ, как это было в случае ПСВ
и.т.д. Поэтому эти интервалы не могут находится на стыке ПСВ, как это было в случае ПСВ .
. ) между вычетами ПСВ(
) между вычетами ПСВ( .
. не может быть больше 4.
не может быть больше 4. 
 ?
?