Максимальные интервалы между взаимно простыми числами

[vicvolf]

Yury_rsn в сообщении #1510350 писал(а):

Я выше сегодня уже описывал идею
- если мы знаем, что для какого-то праймориала максимальный интервал между соседними взаимно простыми с $p_r\#$ числами на всем отрезке от 1 до $p_{r+1}^2$ не превышает p,
то мы можем точно утверждать, что между всеми последовательными квадратами, начиная от $(p_r/2)^2$ обязательно будут расположены простые числа.

Вы хотите сказать, что расстояние между взаимно простыми всегда не превосходит расстояние между простыми, то это очевидно. Пожалуйста, пишите точнее что из этого следует?

[Yury_rsn]

vicvolf в сообщении #1510453 писал(а):

Yury_rsn в сообщении #1510350 писал(а):

Я выше сегодня уже описывал идею
- если мы знаем, что для какого-то праймориала максимальный интервал между соседними взаимно простыми с $p_r\#$ числами на всем отрезке от 1 до $p_{r+1}^2$ не превышает p,
то мы можем точно утверждать, что между всеми последовательными квадратами, начиная от $(p_r/2)^2$ обязательно будут расположены простые числа.

Вы хотите сказать, что расстояние между взаимно простыми всегда не превосходит расстояние между простыми, то это очевидно. Пожалуйста, пишите точнее что из этого следует?

Я это на примере выше объяснял, так, по-моему, понятнее.
Повторю:

1. Тот факт, что, например, для праймориала 197# на отрезке от 1 до $199^2$ максимальный интервал между соседними взаимно простыми с 197# числами меньше 197 означает, что
- где бы он ни был (максимальный интервал) расположен на отрезке от 1 до $199^2$, справа и слева от него будут находиться простые числа,
- формула разности квадратов $(n+1)^2-n^2=2n+1$. Число 197 по этой формуле - ($\approx2n+1$), соответствует разности квадратов $100^2-99^2$. Следовательно, мы можем утверждать, что между $99^2$ и $100^2$ обязательно будет находиться как минимум одно простое число. И точно также это будет верно для всех остальных отрезков между соседними квадратами - между $100^2$ и $101^2$, между $101^2$ и $102^2$, ..., между $198^2$ и $199^2$.

2. Т.е., если для простого числа p известно, что максимальная разность между взаимно простыми с праймориалом p# числами не превышает p,
то это означает, что все интервалы между соседними квадратами от $((p-1)/2)^2$ до $p^2$ содержат простые числа.
Т.е., выполняется гипотеза Лежандра на этих отрезках.

Это, конечно, еще не будет полным доказательством, даже если удасться доказать условие из пункта 2, только промежуточный шаг в эту сторону. Но всё-таки.

[Dmitriy40]

Yury_rsn в сообщении #1510472 писал(а):

2. Т.е., если для простого числа p известно, что максимальная разность между взаимно простыми с праймориалом p# числами не превышает p,

Вряд ли Вы сможете это доказать:

Dmitriy40 в сообщении #1508777 писал(а):

Праймориалы $3\#,5\#,7\#,31\#$ уникальны, в них разница больше его самого (например $34>31$),

А до квадрата следующего простого и $11\#$ тоже:

Dmitriy40 в сообщении #1510341 писал(а):

Используется синтаксис Text

5#:     6       23
7#:     8       89
11#:    14      113
31#:    34      1327

[Yury_rsn]

Dmitriy40 в сообщении #1510476 писал(а):

Yury_rsn в сообщении #1510472 писал(а):

2. Т.е., если для простого числа p известно, что максимальная разность между взаимно простыми с праймориалом p# числами не превышает p,

Цитата:

Вряд ли Вы сможете это доказать:

Почему?
Ваши данные вроде бы подтверждают это наблюдение.

Вот я взял данные из вашей таблицы, пару комментов назад:
163#: 2:179 4:193 6:167 8:359 10:181 12:199 14:293 16:1831 18:523 20:887 22:1129 24:1669 26:2477 28:2971 30:4297 32:5591 34:1327 36:9551 40:19333 42:16141 44:15683 52:19609

Интервалы расположены не по возрастанию. Те, которые с бОльшей разницей, могут встречаться в первый раз раньше, чем с меньшей разницей.
Но максимальный интервал, как видно из ваших расчетов всегда встречается между до $p_{r}^2$ и до $p_{r+1}^2$ (если я не ошибаюсь).

[Dmitriy40]

Yury_rsn
Потому что для праймориалов $p_r\#=\{5\#, 7\#, 11\#, 31\#\}$ максимальная разность на интервале $p_r \ldots p_{r+1}^2$ таки превышает $p_r$. Что прямо противоречит процитированному вашему утверждению. И потребуется доказывать что таких праймориалов-исключений не встретится дальше с ростом $p_r$.

[Yury_rsn]

Dmitriy40 в сообщении #1510508 писал(а):

Yury_rsn
Потому что для праймориалов $p_r\#=\{5\#, 7\#, 11\#, 31\#\}$ максимальная разность на интервале $p_r \ldots p_{r+1}^2$ таки превышает $p_r$. Что прямо противоречит процитированному вашему утверждению. И потребуется доказывать что таких праймориалов-исключений не встретится дальше с ростом $p_r$.

А-а, в этом смысле.
Ну да.
Я это и имел в виду, когда говорил, что то предположение, которое обсуждалось выше - это только шаг в сторону доказательства.
Действительно, надо доказывать, что максимальный интервал строго не превышает определенную границу в каждом праймориале на отрезке от 1 до $p_{r+1}^2$.

Кстати, это граница не p.
На самом деле максимальный интервал для праймориала p# на отрезке от 1 до $p_{r+1}^2$ не должен превышать 2p, чтобы выполнялась гипотеза Лежандра

[vicvolf]

Yury_rsn в сообщении #1510541 писал(а):

[На самом деле максимальный интервал для праймориала p# на отрезке от 1 до $p_{r+1}^2$ не должен превышать 2p, чтобы выполнялась гипотеза Лежандра

Итак Вы рассматриваете интервал от 1 до $p_{r+1}^2$. При $p_r \leq 7$ максимальное расстояние между вычетами на данном интервале, как мы знаем, равно $d=p_{r+1}-1$.

При больших значениях $r$ мы вспоминаем, что на данном интервале мы имеем дело только с простыми числами. На данный момент доказанная верхняя граница между простыми числами на интервале $(1,p^2_{r+1})$ равна $p_{r+1}^{1,05}$. Тогда для выполнения гипотезы Лежандра требуется, чтобы $p^2_{r+1}-(p_{r+1}-1)^2=2p_{r+1}-1>p_{r+1}^{1,05}$. Однако, данное неравенство не выполняется для больших $r$.

Для доказательства гипотезы Лежандра требуется сначала доказать, что верхняя граница между простыми числами на интервале $(1,p^2_{r+1})$ не превосходит $2p_{r+1}-2$, тогда будет выполняться $p^2_{r+1}-(p_{r+1}-1)^2=2p_{r+1}-1>2p_{r+1}-2=2(p_{r+1}-1)=2d$.

[Yury_rsn]

vicvolf в сообщении #1510624 писал(а):

Итак Вы рассматриваете интервал от 1 до $p_{r+1}^2$. При $p_r \leq 7$ максимальное расстояние между вычетами на данном интервале, как мы знаем, равно $d=p_{r+1}-1$.

Подскажите, пожалуйста, откуда это известно?

Цитата:

При больших значениях $r$ мы вспоминаем, что на данном интервале мы имеем дело только с простыми числами. На данный момент доказанная верхняя граница между простыми числами на интервале $(1,p^2_{r+1})$ равна $p_{r+1}^{1,05}$.

Можно уточнить - доказанная верхняя граница величины разности между простыми числами? Я правильно понимаю?
Опять-таки, можно источник привести, пожалуйста.

-- 23.03.2021, 21:01 --

Dmitriy40 в сообщении #1510508 писал(а):

Дмитрий, у вас замечательные способности работать с oeis.
Может, поможете мне найти там аналог вот этой последовательности
6, 15, 21, 33, 54, 75 ... ?
Это одна из модификаций функции Якобсталя.

Напрямую там ее нет, но может быть ваша интуиция подскажет, как ее видоизменить, чтобы найти?

[Dmitriy40]

Yury_rsn в сообщении #1510679 писал(а):

Опять-таки, можно источник привести, пожалуйста.

Есть в вики:

Интервалы между простыми числами писал(а):

Последний результат принадлежит Бакеру, Харману и Пинцу, показавшим, что $\theta$ может быть взято равным 0,525.[10]

Вот и смотрите там 10-й источник.
$1.05$ получаются при учёте квадрата, то число удваивается и даёт это.

[vicvolf]

Yury_rsn в сообщении #1510679 писал(а):

vicvolf в сообщении #1510624 писал(а):

Итак Вы рассматриваете интервал от 1 до $p_{r+1}^2$. При $p_r \leq 7$ максимальное расстояние между вычетами на данном интервале, как мы знаем, равно $d=p_{r+1}-1$.

Подскажите, пожалуйста, откуда это известно?

При $p_r=2$ значение $d=p_{r+1}-1=2$, значение $p^2_{r+1}=9$. На интервале $3,9$ простые $3,5,7$ максимальное расстояние -2.
При $p_r=3$ значение $d=p_{r+1}-1=4$, значение $p^2_{r+1}=25$. На интервале $5,25$ максимальное расстояние между простыми-4.
При $p_r=5$ значение $d=p_{r+1}-1=6$, значение $p^2_{r+1}=49$. На интервале $7,49$ максимальное расстояние между простыми-6.
При $p_r=7$ значение $d=p_{r+1}-1=10$, значение $p^2_{r+1}=121$. На интервале $11,121$ максимальное расстояние между простыми-8.

Сложнее при больших r.

vorvalm в сообщении #1472754 писал(а):

По характеру распределения вычетов ПСВ по модулю $M(p_r)$ максимальную
разность между вычетами надо искать в виде $2p.$
Например, совершенно точно установлено, что в любой ПСВ по модулю $M(p_r)$
есть разности между последовательными вычетами, равными $2p_{r-1}$.
Знаменитая разность $127-113=14$ находится в ПСВ по модулю $11\#$.
Поэтому, нижней границей максимальной разности между вычетами ПСВ
по модулю $p_r\#$ можно считать именно $d=2p_{r-1}$, т.е.

$2p_{r-1}\leqslant d_{\max}$

А вот с верхней границей $d_{\max}$ большие проблемы.
Экспериментальные данные для достаточно больших ПСВ показывают,
что максимальная разность в них может превосходить $2p_r.$
Например, в ПСВ по модулю $43\#$ есть разность $90$, в ПСВ по модулю $83\#$
есть разность $166$, но разности $2p_{r+1}$ в ПСВ по модулю $p_r\#$ пока не найдено
и в качестве гипотезы можно считать, что

$2p_{r-1}\leqslant d_{\max}<2p_{r+1}$

Эти оценки близки к тем, о которых я писал, необходимые для выполнения гипотезы Лежандра $d_{\max}<2p_{r+1}-2$.

[Yury_rsn]

Dmitriy40

Прошу прощения. Наверное, вы могли пропустить.
Поэтому, если можно, повторю просьбу:


"Помогите, пожалуйста, найти в OEIS аналог вот этой последовательности -
6, 15, 21, 33, 54, 75 ...
(Это одна из модификаций функции Якобсталя.)

Напрямую там ее нет, но может быть ваша интуиция подскажет, как ее видоизменить, чтобы найти?"

[Dmitriy40]

Yury_rsn
Я не пропустил, но не представляю как найти. Слишком короток ряд, тут бы большое число. Тривиальные $\pm 1$ не проходят, хотя и находят всего 4 варианта.
Наверное её просто там нет. Не любую модификацию функций туда закидывали (и это правильно, она и так распухла ого-го).

PS. С таким невыделением ника жирным мне не сообщают что меня упомянули, могу и пропустить сообщение. Чтобы правильно вставить ник собеседника в свой ответ достаточно на него (на ник) кликнуть.

[Yury_rsn]

Dmitriy40
Ага, буду иметь в виду
Спасибо!

[vorvalm]

Продолжу историю с разностью $d=40$.
Вычисляя разности по найденным формулам я заметил, что
максимальные разности вплоть до ПСВ ($19\#$) равны $2p_{r-1}$
и при $M=19\# \;\;d_{\max}=34$.
Я определил место этих разностей в ПСВ. Оказалось, что они
образуются на стыках $p_{r-1}\#$, когда числа $n\cdot p_{r-1}\#\pm 1$ кратны
одно $p_{r}$, другое $p_{r-1}$. Эти стыки легко можно вычислить.
А вот когда я с большим трудом вычислил формулу разности $d=38$,
то оказалось этих разностей опять две, но не сходилась сумма
произведений всех разностей на число этих разностей с модулем $23\#$
ровно на 480. Я понял, что это 12 разностей d=40.
Создавать формулу разности $d=40$ я не рискнул, т.к.
на разность $d=38$ была заполнена вычислениями ученическая тетрадь 18 листов
и 3 недели времени. Каждая новая формула увеличивает все затраты в 2 раза.
Я пошел другим путем.
Чтобы определить, есть ли разность $d$ в ПСВ не обязательно создавать ПСВ
и искать в ней эту разность.
Можно поставить вопрос иначе. По данной разности найти ПСВ, в которой эта разность есть.
Для этого надо представить искомую разность $d$ в виде группы вычетов по модулю $M=6.$
Здесь возможны 2 варианта по разностям в группе:
1) 2, 4, 2, 4,.....(0, 2, 6, 8, 12,...$d$)
2) 4, 2, 4, 2,.....(0, 4, 6, 10, 12,...$d$)
Вычеты 0 и $d$ являются крайними вычетами группы и должны оставаться на своих местах.
Остальные вычеты мы будем вычеркивать в зависимости от сравнимости их с простыми числами $p>3$.
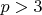
Для этого надо найти цепочки вычетов, сравнимых с простыми модулями $p=5, 7, 11,...$
не затрагивая вычетов 0 и $d.$
Затем распределить эти цепочки так, чтобы они, по возможности, не мешали друг другу,
т.е. имели бы минимум общих вычетов.
Последовательно вычеркивая эти цепочки, мы дойдем до того,
что останутся вычеты, не входящие ни в какие цепочки.
Чтобы вычеркнуть их, на каждый вычет потребуется свое простое число в любом порядке.
Наибольшее простое число, которым будет вычеркнут последний вычет и будет тем $p_r$,
который и определяет ПСВ, в которой есть данная разность $d.$

Пример 1.
$d=40$. Берем группу вычетов с разностями (4,2,4,2...)
(0,4,6,10,12,16,18,22,24,28,30,34,36,40)
Всего вычетов 14. Надо вычеркнуть 12 вычетов.
Определяем цепочки сравнимых вычетов с максимальным числом вычетов.

$p=5,\;(4,24,34),\;\;\;\;\;\;\;\;N=3.$
$p=7,\;(16,30)),\;\;\;\;\;\;\;\;\;\;N=2.$
$p=11,\;(6,28),\;\;\;\;\;\;\;\;\;\;\;N=2.$
$p=13,\;(10,36),\;\;\;\;\;\;\;\;\;N=2$
$p=17,\;(-),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=1$
$p=19,\;(-),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=1.$
$p=23,\;(-),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=1.$


$\sum N=12.$ Следовательно, разности $d=40$ есть ПСВ по модулю $M(23).$
Причем, по числу вычетов, не имеющих цепочек, можно определить число разностей $d$ в данной ПСВ.
Цепочки сравнимых вычетов мы трогать не можем, но свободные простые числа могут менять свои места и число
разностей d равно числу перестановок из этих вычетов.
В нашем случае $P_3=3!=6.$ Но т.к. разность $d=40$ может быть представлена
симметрично, то их число увеличивается до 12.
Этот процесс поддается программированию

Пример 2
$d=90$.
(0,4,6,10,12,16,18,22,24,28,30,34,36,40,42,48,52,54,58,60,64,66,70,72,76,78,82,64,88,90)
Всего вычетов 31. Надо вычеркнуть 29 вычетов.
Определяем цепочки сравнимых вычетов.

$p=5,\;(12,22,42,52,72,82),\;N=6.$
$p=7,\;(4,18,46,60,88),\;\;\;\;\;\;\;N=5.$
$p=11,\;(10,54,76),\;\;\;\;\;\;\;\;\;\;\;\;N=3.$
$p=13,\;(6,58,84),\;\;\;\;\;\;\;\;\;\;\;\;N=3$
$p=17,\;(30,64),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=2$
$p=19,\;(28.66),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=2.$
$p=23,\;(24,70),\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=2.$
$p=29,\;(-),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=1.$
$p=31,\;(16,78),\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=2.$
$p=37,\;(-),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=1.$
$p=41,\;(-),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=1.$
$p=43,\;(-),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N=1.$

$\sum N=29.$ Следовательно, разности $d=90$ есть в ПСВ по модулю $M(43).$
В нашем случае $P_4=4!=24.$ Но т.к. разность $d=90$ может быть представлена
симметрично, то их число увеличивается до 48.

[vicvolf]

Yury_rsn в сообщении #1510541 писал(а):

На самом деле максимальный интервал для праймориала p# на отрезке от 1 до $p_{r+1}^2$ не должен превышать 2p, чтобы выполнялась гипотеза Лежандра

Можете это доказать?