Это надо превратить обратно в 1-форму
Да, с помощью метрики. При этом мы получим в точности

. Не накручиваем ли мы лишние километры?

Формы, в частности, хороши тем, что оба взаимосвязанных утверждения:

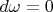
не выводят нас за рамки форм. Поэтому, на мой взгляд, в фразе «
Сказать, что дифференциальная форма  неголономна это всё равно что сказать, что векторное поле
неголономна это всё равно что сказать, что векторное поле  вихревое
вихревое» имело смысл не привлекать

как лишнюю сущность. Тогда, может быть, и
epros не жаловался бы на стиль изложения.
Понятно, что здесь

векторное поле

абсолютно уместно.
В этой системе отсчёта дифференциальная форма времени

неголономна

, более того, она даже не может быть сведена к голономной домножением на интегрирующий множитель

.
Мне понравилось, что Вы различаете эти два случая. Я для себя их когда-то назвал сильной и слабой синхронизируемостью. Диск Эйнштейна не синхронизируем ни в сильном, ни в слабом смысле. Слабо синхронизируема, например, система отсчета Мёллера.
Общепринятых терминов не знаю.



