Но всё ещё хуже. В очередной раз подтверждается, что пионерские работы - сырые. В данном случае, Шварцшильд не довёл расчёты до конца. Он построил метрику, которая сегодня хорошо известна, с переменной

но считал истинной сферической координатой переменную
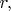
которая связана с ней как

Эта
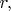
как легко видеть, обнуляется на горизонте чёрной дыры, и поэтому Шварцшильд написал в своей работе, что разрыв метрики успешно сместился в начало координат. Однако, как известно, но ещё не обнаружено в этой работе Шварцшильда,

не является истинной сферической координатой, поскольку поперечные компоненты метрики не обращаются в нуль при

и таким образом, на этом координатном сечении образуют сферу конечной окружности и конечной площади. Для придания более физического смысла радиальной координате, её следует дефинировать так, чтобы она обнулялась вместе с длиной окружности и площадью сферы, а этому требованию удовлетворяет именно координата

Эти нюансы и не тревожили сильно Шварцшильда, поскольку для сравнения с экспериментом он рассмотрел Меркурий (вот о чём я говорил: гравитационное поле в вакууме вокруг небесных тел), и указал, что для него различие

и

имеет порядок

Выяснение же этой детали произошло, очевидно, в последующих работах, возможно, других учёных, и не попало в упомянутый сборник.
А здесь я с Вами спорить не буду, потому что Вы все правильно изложили. Только Шварцшильд не рассматривал протяженное тело ( как у Рашевского или Ландау). У него и статья так называется: "О гравитационном поле точечной массы в Эйнштейновской теории".
(название сборника действительно слегка напутал).
По сути он рассматривал абстрактное многообразие

, где в начало координат (которые он сразу определил

как пространственные и прямоугольные)

, он поместил точечную массу и вырезал эту область, а решение находил вне ее. Но минимальный "размер" этой точки, если так можно выразиться, будет понятен только после введения метрики, то есть после решения уравнений Эйнштейна. В его окончательном варианте метрики , действительно нет разрывов в метрических компонентах и точка

входит в его многообразие ( то есть там и есть "точечная масса").



