Но я не понимаю его физический смысл. Это принципиальное ограничение на точность, с которой мы знаем координату и импульс частицы?
Отдельно координату и отдельно импульс мы можем (в рамках КМ) знать с любой точностью. Иглу сканирующего туннельного микроскопа контролируемо сдвигают на величину меньше диаметра атома. Ограничение есть на возможность одновременного измерения координаты и импульса.
А в чем тогда порочность такого рассуждения: возьмем два электрона, пронумеруем их.
Порочность в том, что электроны нельзя пронумеровать.Прямого эксперимента, доказывающего это, я не знаю, но из этого масса хорошо проверенных следствий (именно из факта невозможности самой нумерации).
Если Вы правильно решите задачу Коши (а я почему-то думаю, что решите), то получите что-то вроде (с точностью до

итп)

Отсюда видно, что "если положение электрона точно известно в настоящий момент времени", т.е. волновая функция является собственной функцией оператора координаты
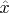
с собственным значением

,
(Оффтоп)
Red_Herring, я все знаю, но так пишут во всех учебниках про импульс, почему нельзя про координату?
то "уже в следующий момент" никакой такой катастрофы не будет. Состояние чуть-чуть размажется вокруг

и боле - ничего. Посему, первые три абзаца можно смело пропустить и начинать с четвертого, а к этим абзацам вернуться, когда все будет прочитано и слегка понято, с целью попытаться угадать, что же на самом деле хотели сказать академики.



