Ещё ни с чем не разбирался. Но вроде методом, который посоветовал epros проще должно получиться.
Попробовал найти решение уравнений Г-Э внутри статической сферической оболочки

, с постоянной плотностью

.
Если искать метрику в виде (

):

То уравнения имеют вид:



Первое интегрируется :

Если вещество покоится, то

и

Согласно Толмену, когда он рассматривает статический шар, он зануляет постоянную

, чтобы не было сингулярности в центре. В данном случае это неважно, поскольку рассматриваем сферическую оболочку.
Из условия сшивки метрика на границе

должна переходить в стандартный Шварцшильд. Значит ,

Откуда постоянная


Радиальная компонента на границе внутри оболочки :

Второе

уравнение дает :

А далее что делать непонятно. Если

на границе внутри и вне оболочки давление равно нулю

, то при тонкостенной сфере наверное можно пренебречь давлением.

или:

Из сшивки с внешним решением
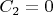
Хотелось бы уточнить, правильно ли решение, как перейти к сингулярной сфере и как далее найти то , что хочет
epros для определения ТЭИ сингулярной сферы.