Во-первых, если я не понимаю, то мне неинтересно и, следовательно, я больше не читаю это.
В том-то и засада, что вы не понимаете, что не понимаете :-) Вам кажется, что вы смутно улавливаете, о чём речь. Примерно как в рассказе:
Цитата:
Сяпала калуша с калушатами по напушке. И увазила бутявку, и волит:
— Калушата! Калушаточки! Бутявка!
Калушата присяпали и бутявку стрямкали. И подудонились. А калуша волит:
— Оее! Оее! Бутявка-то некузявая!
Обычно это даже ещё коварней: вы все слова узнаёте, кроме одного-двух. Например, идёт рассказ про какое-то "топологическое пространство", и вы немножко слышали, что такое топология, представляете себе пространство, и не спотыкаетесь на этом месте. Вам интересно: вам про это топологическое пространство кучу вещей рассказывают. А потом через несколько лет вы в совершенно другой книге читаете определение топологического пространства, и понимаете, что всё, что вы раньше якобы понимали - было совершенно не то и не о том, и всё надо перечитывать с нуля заново. (Пример несколько надуманный, но почти реалистичный.)
Во-вторых, не вижу ничего плохого в том, чтобы перечитывать заново.
Ну, когда вам придётся перечитывать много томов, и жалеть о потраченном времени и силах (ведь всего-то надо было прочитать 1 том перед другими 10), может быть, вы измените своё мнение. Времени и сил всегда не хватает.
В-третьих, мне математика структурно представляется скорее как сеть, а не дерево.
Это я не имею ничего против, если под сетью понимать ориентированный граф или решётку в алгебраическом смысле. По крайней мере, пока речь идёт об определениях, основанных на других определениях.
Ну не могу я просто поверить во что-либо, на чём строится какая-либо теория, не разобравшись в самой этой теории...
Вы ставите телегу впереди лошади. Теория функций действительной переменной строится на действительных числах. Но зачем вам для чисел знать о функциях? Числа можно понять и "поверить в них" сами по себе. А на числах построено много чего разного, не только функции, и так вы утонете в перечислении всех этих вещей, так и не разобравшисть, что такое, собственно, числа.
а она всегда оказывается связанной с несколькими другими
Пускай. Есть параллельные связи: когда теорию

не обязательно знать для изучения теории

а теорию

- для изучения теории

Но при этом они помогают понимать и использовать друг друга, знание обеих этих теорий полезно, и в конце концов, существует теория
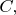
построенная на них обеих, вместе взятых. Например, линейная алгебра и математический анализ (в студенческом объёме) образуют такую пару, и теория дифференциальных уравений уже основывается и на том, и на другом.
Я не о таких связях, я о более сильных: понятия теории

построены на понятиях теории

(и, возможно, теоремах теории

), и определения (и теоремы) прямо цитируют термины, определённые в другой теории.
В-четвёртых, что такого плохого в "смутном понимании"?
Плохого в этом то, что это не понимание вообще! Это иллюзия понимания. Вы или вообще не можете из смутно понимаемых вещей строить самостоятельно рассуждения и вычисления, или иногда "можете", рассматривая правила просто как "игру в символы".
Например, пусть вам не рассказали смысл производной как
![$f'(x)=\lim\limis_{\Delta x\to 0,x^*\to x}[f(x^*+\Delta x)-f(x^*)]/\Delta x,$ $f'(x)=\lim\limis_{\Delta x\to 0,x^*\to x}[f(x^*+\Delta x)-f(x^*)]/\Delta x,$](https://dxdy-02.korotkov.co.uk/f/d/d/f/ddff5bb2f720b8b0f3bb268427b88e0d82.png)
но рассказали, как "приписывать штрих" к алгебраическим выражениям по набору правил. В результате вы "умеете дифференцировать": если вам дать формулу функции, вы с ней повозитесь и выдадите формулу производной. Но вы не будете понимать, для чего это нужно, вы не будете понимать мотивацию производных в случае нескольких переменных, не будете понимать смысл и свойства дифференциальных уравнений, как взять производную от функции, не заданной формулой, как взять производную от разрывной функции, и какой в этом вообще смысл, и так далее. Всё
содержание понятия производной ускользнёт от вас.
Вот встречается где-либо отсылка, пусть даже и в качестве примера, на неизвестный раздел. Так разве не лучше иметь хоть минимальное представление о нём, чем вообще не понимать, и значит мимо пропускать?
Я не про такое "минимальное представление". Это достаточно прочитать статью в
Математической Энциклопедии. Я про чтение учебника по этому разделу насквозь, и потом думание "я знаю этот раздел".
Мне кажется, не имея никакого "пред-знания" нельзя ничего вообще узнать. Обучение мне представляется как постоянное более глубокое познание какой-либо темы. А начинать с чего-то ведь надо.
Эта вся хвилософия не имеет отношения к тому, что я сказал. Я говорил про вполне конкретные вещи. Если хотите пример последовательности обучения, в которой сбалансированы введения и углубления, то это многие вузовские программы по математике. Они не лишены недостатков, но в целом идут от простого к сложному, и от базового к производному. Часто они отлажены многолетней практикой. Разумеется, я не призываю буквально следовать стандарту, но ориентироваться на него стоит - он всё-таки не полнейшая глупость.
А в-пятых, боясь, что либо "неправильно" и не вовремя узнать (в моём случае) просто на просто ничего и не будешь узнавать.
А я и не предлагаю бояться. Я предлагаю здраво оценивать свои результаты, не переоценивать их. Например, вы скорей всего нормально знаете логику и теорию множеств, но скорей всего понятия не имеете о категориях и топосах - эти книги в вашем списке выглядят случайными и несвоевременными. Чтение Александрова, а возможно, и Гильберта, Коэна, кого-то ещё, - для вас имеет мало смысла. Это будет максимум "душеспасительное чтение", помогающее улавливать "дух" математики и некоторые общие идеи, но содержание этих книг пройдёт мимо вас.
Ну а поскольку вы считаете, что можно построить башню знаний, то прошу, дайте последовательный список литературы или ссылок (или ссылок на литературу) в том самом порядке, начиная от школьных основ математики. Можно и с комментариями - для чего и когда и как данный труд осваивать.
О, вот это огромный вопрос. Ответы на него всё-таки бывают разные, в зависимости от личных вкусов (касательно выбора конкретных учебников), в зависимости от конечной цели ("башня" "ветвится", и к разным "веткам" ведут разные "пути"), в зависимости от других нюансов. На эту тему на форуме есть темы "подскажите литературу", гуляют в народе разные списки литературы и т. п.
Я чувствую себя достаточно уверенно только в самых нижних этажах математики (1-3 курс, может быть), вот по физике мог бы ответить полнее. И в любом случае, мои ответы хуже, чем у многих других участников этого форума. Поэтому я лучше не отвечу ничего конкретного, а переадресую вас к другим участникам. Теперь вы знаете правильный вопрос, и можете с него начинать.
Скажу только, что со школьным курсом математики можно порвать решительно и без сожалений, он практически ничего не даёт, весь материал школьного курса проходится в вузе заново, уже на другом уровне систематичности и строгости.
А я вот без оснований не могу. Меня постоянно одолевают сомнения о правильности тех или иных рассуждений (логических выводов) или (что тоже очень часто) о подстановках символов – что встречается всюду.
Для этого вам достаточно прочитать тщательно учебники для первого курса, предназначенные для математиков (например, для мехматов). Там строгости рассуждений уделено достаточно внимания. Если вы и в них будете сомневаться - это уже паранойя :-)



