Уважаемый Гаджимурат
1.Впечатляет!
Это все так...пустое.Вот для 5 степени и выше появляется еще уравнения для

,вот это уравнения для

-й степени впечатляет.Половину страницы надо исписать,что бы показать ее суть.Так для 5 степени

.
Здесь

,а

для случая ,когда примем,что

делится на 5. И

. Кстати вот почему нет решения для 1 случая Ферма для 5 степени.Так как при этом случае

,здесь уже

,а

и

или

(1) делится на 5,но и

(2)тоже должно делится на 5,Возведем (1) в квадрат и вычтем из (2) получим,что и

делится на 5,а это невозможно,потому что

взаимно простые числа и не имеют общего делителя!! и не делятся на 5,а если

либо

можно разделить на 5,то и

или
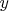
будет делиться на 5,что противоречит поставленному условию.Кстати,никто не говорил,а что должно делиться на степень при 1 случае Ферма.Нет,писали что для определенных групп

должно делиться на степень и все!!.Я знаю,что должно делиться при 1 случае Ферма....

делится на рассматриваемую степень,а для нее есть формула,что я и написал для 5 степени!!. Для второй и третьей степени

. Вот почему легко можем сказать,что для 2 и 3 степени 1 случай Ферма не стоит рассматривать!!....

, а 1 не делится ни на 2,ни на 3 !!
-- Вс дек 08, 2013 20:39:40 -- Гаджимурат, вы личность наивная.
Не без этого.Со знанием математики за среднюю школу с оценкой 3 и ВТФ!!.Но вот что интересно,многое доказал,что было доказано до меня,но я доказал гораздо проще и много чего доказал для 1 случая ферма!!.Ищу доказательство третьей степени,свое...пока не удачно,старый стал.Чем в деревне заниматься,не водку же пить!!.Спасибо интернету,многое посмотрел и увидел...про ВТФ тоже !!.Кстати,это я посоветовал писать доказательства для 3 степени.Все просто,если доказал ВТФ,то покажи это доказательство на 3 степени...проверить очень легко!!.Многие все равно пишут длинные формулы для

степени и искать ошибку тяжело.



