Чтобы определить, есть ли разность

в ПСВ не обязательно создавать эту ПСВ и искать в ней

Можно поставить вопрос иначе. По данной разности найти ПСВ, в которой эта разность есть.
Для этого надо представить искомую разность

в виде группы вычетов по модулю

Здесь возможны 2 варианта по разностям в группе:
1) 2, 4, 2, 4,.....(0, 2, 6, 8, 12,...

)
2) 4, 2, 4, 2,.....(0, 4, 6, 10, 12,...

)
Вычеты
0 и

являются крайними вычетами группы и должны оставаться на своих местах.
Остальные вычеты мы будем вычеркивать в зависимости от сравнимости их с простыми числами
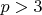
.
Для этого надо найти цепочки вычетов, сравнимых с простыми модулями

не затрагивая вычетов
0 и

Затем распределить эти цепочки так, чтобы они,по возможности, не машали друг другу,
т.е. имели бы минимум общих вычетов.
Последовательно вычеркивая эти цепочки, мы дойдем до того,
что останутся вычеты, не входящие ни в какие цепочки.
Чтобы вычеркнуть их, на каждый вычет потребуется свое простое число в любом порядке.
Наибольший простой модуль, которым будет вычеркнут последний вычет и будет тем

,
который и определяет ПСВ, в которой есть данная разность

Пример.
Возьмем

. Берем группу вычетов с разностями (4,2,4,2...)
(0,4,6,10,12,16,18,22,24,28,30,34,36,40,42,48,52,54,58,60,64,66,70,72,76,78,82,64,88,90)
Всего вычетов 31. Надо вычеркнуть 29 вычетов.
Определяем цепочки сравнимых вычетов с максимальным числом вычетов.













Следовательно, разности

есть ПСВ по модулю

Причем, по числу вычетов, не имеющих цепочек, можно определить число разностей

в данной ПСВ.
Это число равно числу перестановок из этих вычетов.
В нашем случае

Но т.к. разность

может быть представлена
и группой по разностям 2, 4, 2, 4,..., то их число увеличивается до 48.
Этот процесс поддается программированию.