О проблеме Гольдбаха

[vicvolf]

vorvalm в сообщении #1601484 писал(а):

Принимаем $p^2_{r+1}=a_n$, тогда $a_n-a_{n-1}<p_{r+1} - 1$

Возьмем $p_r=13$, тогда $p_{r+1}=17$. В этом случае $a_n-a_{n-1}=p^2_{r+1}-p^2_{r}=17^2-13^2=289-169=120$, а $p_{r+1} - 1=17-1=16$.
Поэтому в этом случае наоборот $a_n-a_{n-1}=120>p_{r+1} - 1=16$. Может я не совсем правильно понял, тогда, пожалуйста, поясните.

[Cantata]

Подскажите, пожалуйста, в гипотезе Гольдбаха один из вопросов - не может ли так быть, что на месте простого числа будет составное и поэтому неизвестно могут ли все чётные числа быть представлены в виде суммы двух простых чисел?

Просто я сейчас смотрю на свои простые выкладки и у меня получается, что у каждого чётного числа есть свой предел, сверх которого составные числа не участвуют в сложении, хотя простые числа, которые стоят дальше в числовом ряду, вполне вписываются.

Мне, наверное, проще показать наглядно свою логику - в небольших табличках, чем пытаться объяснить что я имею ввиду.
Может кто готов посмотреть и подсказать насколько тривиальные у меня выводы?

[Батороев]

Cantata в сообщении #1700941 писал(а):

Просто я сейчас смотрю на свои простые выкладки и у меня получается, что у каждого чётного числа есть свой предел, сверх которого составные числа не участвуют в сложении, хотя простые числа, которые стоят дальше в числовом ряду, вполне вписываются.

Сомнительно, а потому любопытно.

[Cantata]

Батороев, вы правы, что сомневаетесь. Я уже поняла, что сделала ошибочные выводы

Моё предположение основывается на том, что интервал, состоящий из нечётного количества простых чисел, можно сравнить с полным интервалом натуральных чисел, у которого такое же центральное число, как и у интервала с простыми числами и, взяв разницу их сумм, увидеть какие составные включены, а какие нет.
Но, как я потом поняла свою ошибку, таким образом я все равно не могу понять - является ли число простым или нет. Поэтому постараюсь кратко описать свои мысли, но уже не знаю, насколько они будут интересны.

Решила посмотреть на ряд натуральных чисел, который начинается с $2$, а потом идет от $3$ с шагом $+2$, т.е. все числа, кроме первого, нечётные. Ряд начинается с $2$ чтобы его можно было сравнить с рядом из простых чисел.
$2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27..$

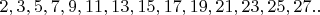
Потом подумала, что если каждое из чисел данного ряда является центральным для своего симметричного интервала, обозначу его как С:
$[2, 3, 5]$, центральное C = $3$
$[2, 3, 5, 7, 9]$, центральное C = $5$
$[2, 3, 5, 7, 9, 11, 13]$, центральное C = $7 $
$[2, 3, 5, 7, 9, 11, 13, 15, 17]$, центральное C = $9$
$[2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]$, центральное C = $11$ и т.д.

Для краткости такие интервалы буду называть – полными.
Теперь складываю попарно симметричные числа, получаю чётные числа и суммирую их, находя сумму каждого интервала.
И вижу, что разница между соседними суммами каждого интервала равна $8n$,
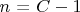
где $n$ = $C-1$, т.е. если взять центральное число $C =7$, то сумма его интервала вырастет на $8 \cdot6$.
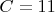
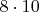
У интервала с $C = 11$ сумма увеличится на $8 \cdot10$ и т.д.
Или эту разницу можно представить как сумму двух крайних правых чисел интервала, умноженных на $2$.

Взяла, для примера, интервал с простыми числами и центральным $C = 17 [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41]$.
Сумма его парных чисел равна $476$.
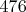
Сумма парных чисел полного интервала с центральным $C = 17 [2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33]$ равна $580$.

Разница $D = 580 - 476 = 104$
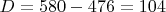
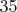
Видим, что в полный интервал не входят числа $35$ и $39$, хотя интервал с простыми включает в себя числа $37$ и $41$.

$(9+15+21+25+27+33)-(37+41)=52\cdot2$

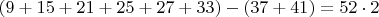
И получила искомую разницу между двумя интервалами.
Возможно, что я искусственно подгоняю результаты, т.к. на большом количестве интервалов не проверяла.

[Батороев]

Cantata в сообщении #1700987 писал(а):

Но, как я потом поняла свою ошибку, таким образом я все равно не могу понять - является ли число простым или нет.

Это и составляет основную проблему.
Успехов!
p.s. Чтобы не захламлять чужие темы, рекомендую заводить собственные. А ТС-а прошу извинить!

[Cantata]

Батороев
Спасибо!

[Cantata]

Cantata в сообщении #1700987 писал(а):

Разница $D = 580 - 476 = 104$
Видим, что в полный интервал не входят числа $35$ и $39$, хотя интервал с простыми включает в себя числа $37$ и $41$.

$(9+15+21+25+27+33)-(37+41)=52\cdot2$

И получила искомую разницу между двумя интервалами.

Посмотрела несколько интервалов, которые идут подряд, и, мне кажется, что это такой способ компенсации.
Когда часть составных чисел, идущих до максимального числа полного интервала отсеивается, то новые простые числа их компенсируют своим весом,
чтобы сохранить симметрию и общую сумму в интервале. Поэтому могу предположить, что новые числа действительно будут только простыми.

Может мне нужно создать новую тему и более подробно расписать то, как я понимаю? У меня нет таких навыков, поэтому для меня это достаточно сложно. Но я соберусь с мыслями и попробую оформить более правильно.

Задумалась над тем - можно ли доказать, что простые числа, образуемые такими симметричными интервалами, идут непрерывно
и можно ли сделать выводы, что сам принцип компенсации даёт повод думать, что простые числа бесконечны?

Или мои выводы о способе компенсации неверные и можно на этом и закончить?)

[Cantata]

Вчера меня озарило, что я могу делать любые проверки своей идеи и они будут верны.
Но неверно изначально заданное условие, которое я сама же и создаю.
Естественно будут в результате появляться все "новые" простые числа, я же сама их добавила, чтобы сравнить два интервала.
Всё оказалось тривиально.

[Утундрий]

Cantata в сообщении #1701697 писал(а):

меня озарило, что я могу делать любые проверки своей идеи и они будут верны.

Проверки или идеи?

[Cantata]

Утундрий
В ходе проверки моя идея не нашла подтверждения.
Причиной послужила моя некорректная постановка исходных условий