Попробуем разобраться с этой задачей.
Гравитационными эффектами и вообще тем, что самолёт летит на некоторой высоте над поверхностью Земли, пренебрегаем.
Исходные данные возьмём из
первого сообщения темы с одной поправкой (

и

измеряются в той ИСО, в которой центр Земли покоится):

с - звёздные сутки (
на двухтысячный год),

м - длина параллели, по которой летит самолёт,

м/с - скорость точки поверхности Земли на этой параллели (здесь
petrovich1964 допустил ошибку: для определения скорости точки поверхности Земли или угловой скорости вращения Земли в ИСО нужно использовать звёздные сутки, а не солнечные),

м/с - собственная скорость самолёта (измеряется в мгновенно сопутствующей ИСО той точки поверхности Земли, "в которой" находится самолёт).
Другие обозначения:

м/с - скорость света,

- радиус параллели, по которой летит самолёт,

- угловая скорость вращения Земли.
ИСО, в которой центр Земли неподвижен.
Сначала рассмотрим инерциальную систему отсчёта

, в которой центр Земли покоится. В этой ИСО расчёты наиболее просты, так как все рассматриваемые часы движутся с постоянными по величине (но не по направлению) скоростями. Считаем, что центр Земли совпадает с началом координат

, плоскость экватора совпадает с плоскостью

, система координат

правая, Земля вращается против часовой стрелки, если смотреть на неё из полупространства

. Предполагаем, что параллель, по которой летят самолёты, находится в плоскости

(конкретное значение

нам не понадобится).
Скорость самолёта, летящего на восток:

скорость самолёта, летящего на запад:

Возвращению самолёта на аэродром соответствует тот момент времени, в который разность путей, пройденных самолётом и аэродромом, будет равна длине параллели, то есть,

.
Время полёта самолёта, летящего на восток:

время полёта самолёта, летящего на запад:

(мы здесь предполагаем, что, в соответствии с условием задачи,

). Обратите внимание, что

, причём, разность

не зависит от собственной скорости самолёта (это так называемый эффект Саньяка; последнее выражение совпадает с формулой (4) в работе
http://ufn.ru/ru/articles/2000/12/c/). Для приведённых выше данных получаем

с.
В СТО и ОТО промежуток времени, измеряемый движущимися часами, вычисляется по формуле

где

- отрезок мировой линии, для которого вычисляется собственное время, а выражение для интервала

зависит от используемой системы отсчёта. Если эта система отсчёта инерциальная, а пространственные координаты декартовы (как это обычно и бывает по умолчанию), то

(

- пространственная метрика). В этом случае получаем

где

- скорость движения часов,

и

- временнáя координата начальной и конечной точек дуги

. В рассматриваемом в этом пункте случае скорость

постоянна, поэтому последнее выражение превращается в

Воспользуемся последней формулой.
Для самолёта, летящего на восток,

, поэтому время, измеренное аэродромными часами, равно

а время, измеренное самолётными часами, равно

Для самолёта, летящего на запад,

, поэтому время, измеренное аэродромными часами, равно

а время, измеренное самолётными часами, равно

Сравнивая величины (8) - (11), получаем следующие выводы.
Так как

, первым на аэродром вернётся самолёт, летевший на запад. Другой самолёт вернётся с запозданием на

(последнее выражение совпадает с формулой (5) упомянутой выше статьи
http://ufn.ru/ru/articles/2000/12/c/).
При этом показания часов восточного самолёта в момент посадки на аэродром такие же, как часов западного в момент его посадки, поскольку из формул (9) и (11) следует, что

. Однако западный самолёт к этому времени уже находится на аэродроме в течение

с, поэтому часы, летевшие на восток, будут показывать меньшее время, чем часы, летевшие на запад, на указанную величину. (Не нужно удивляться тому, что с указанной точностью

: они отличаются на

с.)
Таким образом, показания самолётных часов после их возвращения на аэродром вовсе не совпадают, как утверждает
petrovich1964, а отличаются на

с, причём, часы, летевшие на восток, показывают меньшее время, чем летевшие на запад.
Сравним показания аэродромных часов с показаниями самолётных часов в момент посадки.
Для самолёта, летевшего на восток:

Для самолёта, летевшего на запад:

Таким образом, в момент посадки восточного самолёта его часы будут отставать от аэродромных на

с, в то время как в момент посадки западного самолёта его часы будут опережать аэродромные на

с. (Для упрощения выражений в формулах (13) и (14) использована известная приближённая формула

, погрешность которой меньше

при
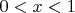
и меньше

при

; корень в знаменателе заменён единицей.)
Предположим теперь, что самолёт, летящий на запад, достигнув аэродрома, не садится, а продолжает полёт в западом направлении до встречи с самолётом, летящим на восток. По часам рассматриваемой ИСО встреча произойдёт спустя время

после старта. Используя снова формулу (7), получим, что самолёт, летящий на восток, достигнет точки встречи за время

по своим часам, а самолёт, летящий на запад - за время

по своим часам. Таким образом, в момент встречи разница показаний часов на этих самолётах равна

Подставляя исходные данные, получим

с (это число нам уже два раза встречалось; оно отличается от двух предыдущих на очень малую величину).
Собственно говоря, на этом можно бы и закончить. Тот, кто немного разбирается в вопросе, понимает, что показания часов ни от каких систем отсчёта не зависят. Тот, кто немного разбирается в математическом анализе, также понимает, что величина криволинейного интеграла (4) также не зависит от выбора системы отсчёта. Поэтому нет нужды вычислять то же самое в каких-либо других системах отсчёта. Однако профаны наподобие
petrovich1964 придают какое-то магическое значение манипуляциям с системами отсчёта. Им почему-то кажется, что в другой системе отсчёта может получиться что-то другое. И получается, поскольку ведь считать-то надо уметь...
Если у меня найдётся свободное время, посчитаю то же самое в других системах отсчёта. Хотя бы частично.



