А.А.Зенкин, "Ошибка Георга Кантора". - Вопросы философии, 2000, No. 2, 165-168.
Текст можно найти здесь:
http://alexzen.by.ru/papers/vf1/vf-rus.html.
Видимо, это сайт автора. Все цитаты со ссылкой на Зенкина взяты с указанной страницы сайта.
Я перенабрал в цитатах все формулы, заменив символы "О" и "®" в тексте Зенкина общепринятыми символами "

" и "

" (видимо, символы "О" и "®" появились из-за неправильного отображения на сайте).
Также я буду ссылаться на две книги (на вторую из них ссылается и Зенкин).
[1]. Георг Кантор. Труды по теории множеств. Москва, "Наука", 1985.
[2]. Стефен К.Клини. Введение в метаматематику. Москва, "Иностранная литература", 1957.
А.А.Зенкин писал(а):
Приведу полный текст этой знаменитой Теоремы Кантора и ее доказательства.
Обозначим через

множество всех действительных чисел, или, что то же, всех точек единичного отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Введем следующие соглашения. Для простоты мы будем использовать двоичную систему представления действительных чисел. Вместо длинного выражения "действительное число x является элементом множества

" будем писать
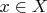
. Исключительно для удобства последующих ссылок будем использовать различные записи, заключенные в фигурные скобки.
Итак, рассмотрим традиционное доказательство Теоремы Кантора (см., например, С.К.Клини, "Введение в метаматематику", М.: ИЛ, 1957, стр. 13).
ТЕОРЕМА КАНТОРА: {Тезис A:} Множество

- несчетно.
ДОКАЗАТЕЛЬСТО КАНТОРА. Допустим противное, т.е. что {допущение метода от противного НЕ-A:} множество

- счетно. Это, по определению, означает, что все его элементы можно занумеровать с помощью обычных конечных натуральных чисел.
Пусть последовательность

является некоторым таким пересчетом всех
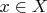
, т.е.,
{ B:} для любого

, если

, то

является элементом последовательности (1), или, короче,

.
Далее, применяя свой знаменитый диагональный метод к пересчету (1), Г.Кантор строит новое, так называемое "диагональное" действительное число (ДДЧ), скажем,

такое, что, по определению,

, но, по построению,

отлично от каждого элемента пересчета (1), т.е. ДДЧ

не принадлежит пересчету (1). Следовательно,
{НЕ-B:} данное ДДЧ

, но это ДДЧ

не входит в пересчет (1).
Итак, получено противоречие между НЕ-B and B. Из этого противоречия, с учетом произвольности выбора пересчета (1), Кантор делает свой знаменитый вывод: допущение НЕ-А о счетности множества

- ложно. Следовательно, {A:} множество

- несчетно. Ч.Т.Д.
В первой фразе цитаты Зенкин обещает привести полный текст теоремы Кантора и её доказательства. Однако на самом деле полного текста доказательства нет. Вторая фраза сформулирована, как минимум, неаккуратно, поскольку в ней утверждается, что множество всех действительных чисел совпадает с множеством точек отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
.
Выбор двоичной системы счисления допустим, но
создаёт некоторые проблемы, и, ввиду отсутствия самой существенной части текста доказательства, не видно, как они преодолеваются. Это очень жаль, так как после процитированного доказательства Зенкин излагает ещё некоторые рассуждения, осмысленность которых зависит от опущенных им деталей.
Далее Зенкин утверждает, что приведённое им доказательство принадлежит самому Кантору, но ссылается почему-то на книгу Клини. На основании этого, видимо, можно предположить, что Клини переписал это доказательство из одной из работ Кантора, а Зенкин процитировал Клини. Позже посмотрим, что написано у Кантора и у Клини.
Как видим, Зенкин настаивает на том, что Кантор доказывает теорему методом "от противного", причём, именно так, как это изложено у Зенкина ("доказательство Кантора"). В этом доказательстве присутствуют 4 "тезиса": {A:}, {НЕ-A:}, {B:}, {НЕ-B:}. Тезис {B:} просто утверждает, что выбранная последовательность действительных чисел включает все действительные числа, то есть, является следствием {НЕ-A:}, а не самостоятельным предположением. Соответственно, когда в результате применения диагонального метода получается утверждение {НЕ-B:}, противоречащее {B:}, по правилам математической логики из него получается {A:}, то есть, утверждение теоремы. Всё ли здесь в порядке?
Заметим, что диагональный метод в стандартном варианте никаким способом не использует тезис {B:}. Этот метод применяется к произвольной последовательности действительных чисел и (
если мы об этом позаботились) даёт число, не содержащееся в последовательности. То есть, утверждение {НЕ-B:} получается без какого-либо участия тезисов {B:} или {НЕ-A:}. С таким же успехом мы могли бы начать доказательство фразой "Пусть

- произвольная последовательность действительных чисел." Применив диагональный метод, мы получили бы действительное число, не входящее в эту последовательность, то есть, утверждение {НЕ-B:}, и, сославшись на
определение 18, сделали бы вывод о несчётности множества действительных чисел.
Таким образом, доказательства "от противного" по сути здесь нет, есть только некая формальная видимость. Мы можем спокойно сформулировать тезисы {НЕ-A:} и {B:} в любом место доказательства, в том числе, после доказательства утверждения {НЕ-B:}, и заявить о получении противоречия. Разумеется, если сразу после доказательства некоторого утверждения сформулировать противоречащее ему, то получится противоречие (кстати, такие рассуждения встречаются). Зачем, собственно говоря, это понадобилось Зенкину? Да просто иначе ему было бы нечем манипулировать в последующих рассуждениях.
Прежде чем продолжать читать Зенкина, посмотрим на доказательство, изложенное у Клини. Зенкин ссылается именно на это доказательство.
С.К.Клини в [2] писал(а):
Посредством знаменитого "диагонального метода" Кантора было доказано, что в математике рассматриваются и такие бесконечные множества, которые не могут быть пересчитаны. Множество
действительных чисел несчетно.
Рассмотрим сначала действительные числа

в полуинтервале

. Каждое действительное число из этого полуинтервала однозначно представляется посредством некоторой правильной бесконечной десятичной дроби, т. е. десятичной дроби, первая значащая цифра которой стоит правее запятой и в которой имеется бесконечно много цифр, отличных от

. Число может представляться в виде конечной десятичной дроби, т. е. дроби с повторяющимися нулями, но такую дробь можно заменить на бесконечную с повторяющимися девятками. Например,

или

можно заменить на

. Обратно, каждая правильная бесконечная десятичная дробь представляет единственное число из этого полуинтервала.
Допустим теперь, что

— бесконечный перечень или пересчет некоторых, но не обязательно всех, действительных чисел, принадлежащих этому полуинтервалу. Напишем теперь одну под другой соответствующие им бесконечные десятичные дроби
![$\xymatrix{0,&x_{00}\ar[rd]&x_{01}&x_{02}&x_{03}&\ldots\\ 0,&x_{10}&x_{11}\ar[rd]&x_{12}&x_{13}&\ldots\\ 0,&x_{20}&x_{21}&x_{22}\ar[rd]&x_{23}&\ldots\\ 0,&x_{30}&x_{31}&x_{32}&x_{33}\ar[rd]&\ldots\\ \ldots&\ldots&\ldots&\ldots&\ldots&\ldots}$ $\xymatrix{0,&x_{00}\ar[rd]&x_{01}&x_{02}&x_{03}&\ldots\\ 0,&x_{10}&x_{11}\ar[rd]&x_{12}&x_{13}&\ldots\\ 0,&x_{20}&x_{21}&x_{22}\ar[rd]&x_{23}&\ldots\\ 0,&x_{30}&x_{31}&x_{32}&x_{33}\ar[rd]&\ldots\\ \ldots&\ldots&\ldots&\ldots&\ldots&\ldots}$](https://dxdy-04.korotkov.co.uk/f/3/8/0/380167748bacac2453df2c21d85a66bb82.png)
Образуем диагональную дробь, указанную стрелками. Заменим в ней каждую из последовательных цифр

на отличную от нee цифру

так, чтобы при этом не получилась конечная дробь. Например, пусть

, если

, и

, если

.
Полученная дробь

представляет некоторое действительное число

, которое принадлежит нашему полуинтервалу, но не входит в рассматриваемый пересчет. Действительно, эта дробь отличается от первой из данных дробей своей первой цифрой после запятой, от второй — своей второй цифрой после запятой, от третьей — третьей цифрой после запятой и т. д.
Поэтому данный пересчет не является пересчетом всех действительных чисел полуинтервала

. Пересчета всех действительных чисел этого полуинтервала не существует.
Это классическое доказательство несчётности множества действительных чисел диагональным методом. Никаких намёков на доказательство "от противного" здесь нет, более того, Клини подчёркивает, что рассматривается "бесконечный перечень или пересчет некоторых, но
не обязательно всех, действительных чисел, принадлежащих этому полуинтервалу". Термин "перечень" или "пересчёт" у Клини предполагает, что все члены последовательности

попарно различны, поэтому заключительное утверждение доказательства Клини соответствует
определению 19.
Как понимать тогда слова Зенкина: «рассмотрим традиционное доказательство Теоремы Кантора (см., например, С.К.Клини, "Введение в метаматематику", М.: ИЛ, 1957, стр. 13)»?
А.А.Зенкин писал(а):
К сожалению, знаменитый диагональный метод Кантора не учитывает и не использует количественных характеристик (т.е. мощности) тех множеств, к которым он применяется (см. [1,2,4]). Поэтому в рассматриваемом случае Кантор, для получения вожделенного противоречия, использует только актуальность пересчета (1), т.е. условие, что пересчет (1) "содержит все
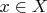
".
Ну, как мы видели, диагональный метод не нуждается в этом условии, и, более того, Клини, на которого ссылается Зенкин, на это явным образом указывает. Так что здесь Зенкин просто умышленно врёт (прошу прощения за непарламентские выражения). Потом мы увидим, что и сам Кантор без этого условия прекрасно обходится и также не получает никакого "вожделенного противоречия".
А.А.Зенкин писал(а):
Тривиально очевидно, что для пересчета (1) в двоичной системе можно построить только единственное ДДЧ

.
Это, извините, смотря как строить. Легко можно построить и больше.
А.А.Зенкин писал(а):
С другой стороны, согласно канторовскому определению понятия бесконечного множества, мощность последнего не изменится, если к нему добавить … один новый элемент.
Поэтому мы можем добавить ДДЧ

к исходному счетно-бесконечному пересчету (1), например, таким образом:

Очевидно, что теперь новый счетно-бесконечный пересчет (1.1) будет содержать все действительные числа множества

, т.е.
{B:} для любого

, если

, то

.
А это, извините, уже совсем глупо. Если какой-то метод даёт единственный элемент множества, то ниоткуда не следует, что там нет других элементов. Поэтому никакого {B:} не получается.
Поэтому на этом месте бесконечная цепочка рассуждений Зенкина
А.А.Зенкин писал(а):
обрывается, едва начавшись - на первом же {НЕ-B:}. Поэтому последующие его выводы оказываются ни на чём не основанными, высосанными из пальца.
Есть ещё продолжение этого рассуждения для случая, когда используется не двоичная система счисления.
А.А.Зенкин писал(а):
Очевидно, что если мы возьмем не двоичную, а любую другую систему счисления с основанием больше 2, то для любого данного счетного пересчета (1) Кантор сможет построить уже не единственное ДДЧ, а бесконечное множество ДДЧ, скажем, множество

.
Здесь Зенкин рассматривает два случая: когда

счётно и когда

несчётно. Второй случай он отвергает на том основании, что его "требуется доказать", не замечая, что точно так же "требуется доказать" и первый случай. Правда, все эти рассуждения убиваются тем обстоятельством, что если диагональный метод даёт некоторое множество

действительных чисел, не содержащихся в заданной последовательности, то ниоткуда не следует, что множество

содержит все такие числа. А также изначальной никчёмностью этих рассуждений, поскольку доказательство теоремы Кантора закончилось в тот момент, когда было построено число (одно!), не содержащееся в произвольно взятой последовательности - согласно определению несчётного множества.
Доказательство несчётности множества действительных чисел у Кантора встречается два раза: в статьях "Об одном свойстве совокупности всех действительных алгебраических чисел" (стр. 20 - 21) и "О бесконечных линейных точечных многообразиях" (стр. 43 - 45). Я приведу первое из них, поскольку оно намного короче. Третий раз (в статье "Об одном элементарном вопросе учения о многообразиях", стр. 170 - 171) Кантор пишет, что эту теорему можно доказать значительно проще, после чего рассматривает применение диагонального метода для доказательства несчётности множества двоичных последовательностей и обобщение этого метода на функции, определённые на произвольном множестве и принимающие два различных значения. Как отсюда вывести теорему о несчётности множества действительных чисел, Кантор не объясняет, но все необходимые для этого утверждения в предшествующих работах Кантора доказаны.
Г.Кантор в [1] писал(а):
Если по какому-нибудь закону задана бесконечная последовательность отличных друг от друга числовых величин

то во всяком заданном интервале

можно определить число
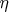
(а значит, и бесконечно много таких чисел), которое не содержится в последовательности (4). Это и предстоит теперь доказать.
Мы начинаем с произвольно заданного интервала

, и пусть

. Два первых числа последовательности (4), которые расположены в этом интервале (за исключением концов), можно обозначить через
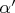
,

, и пусть

; аналогично два первых числа нашей последовательности, расположенных внутри

, обозначим через

,

, и пусть

; по тому же закону образуем следующий интервал

и т. д. Здесь, следовательно,

по самому определению являются определенными числами нашей последовательности (4), индексы которых все время возрастают; то же самое справедливо для чисел

. Примем, далее, числа

возрастающими по величине, а числа

убывающими по величине. Каждый из интервалов

содержит в себе все следующие за ним. Теперь мыслимы только два случая.
Или число построенных таким образом интервалов конечно, и пусть последний из них будет

. Так как внутри него может быть расположено самое большее одно число последовательности (4), то в этом интервале можно взять число, не содержащееся в последовательности (4), и тем самым для этого случая теорема доказана.
Или число построенных интервалов бесконечно. Тогда числа

, поскольку они возрастают по величине, не возрастая до бесконечности, имеют определенный предел

; то же самое верно для чисел

, так как они убывают по величине, и пусть их предел

.
Если

(случай, имеющий место для совокупности

всех действительных алгебраических чисел), то легко убедиться, обратившись к определению интервала, что число

не может содержаться в нашей последовательности. Если же

, то всякое число
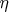
внутри интервала

или на его границе удовлетворяет выставленному требованию не содержаться в последовательности (4).
Здесь нет ни доказательства "от противного", столь красочно расписанного Зенкиным, ни диагонального метода. Кантор строит действительное число, не содержащееся в произвольно заданной последовательности попарно различных действительных чисел, используя свойства множества действительных чисел, известные из курса математического анализа. Утверждение теоремы, таким образом, соответствует
определению 19 несчётного множества.
Я не буду приводить второго доказательства Кантора, поскольку оно существенно длиннее, но по сути мало отличается от процитированного. Желающие могут взять сборник работ Кантора и убедиться, что там тоже нет ни доказательства "от противного", ни диагонального метода.
А вот диагональный метод (стр. 170 - 171).
Г.Кантор в [1] писал(а):
... если

и
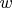
— два каких-либо исключающих друг друга признака (Charaktere), то рассматриваем совокупность

элементов

зависящих от бесконечно многих координат

, где каждая из этих координат есть

или
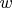
. Пусть

— совокупность всех элементов

.
Элементами совокупности М являются, например, три следующие:



Теперь я утверждаю, что такое многообразие

не имеет мощности последовательности

.
Это вытекает из следующей теоремы:
«Если

— какая-либо просто бесконечная последовательность элементов многообразия

, то всегда существует такой элемент
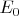
многообразия

, который не совпадает ни с каким

».
Пусть





Здесь

суть определенно

или
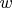
. Определим теперь последовательность

так, чтобы

был тоже равен только

или
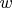
и отличен от

.
Итак, если

, то

, а если

, то

.
Если теперь мы рассмотрим элемент

многообразия

, то очевидно, что равенство

не может иметь места ни для какого положительного целочисленного значения
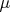
, так как в противном случае для соответствующего
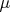
и для всех целочисленных значений

было бы

а значит, в частности,

что исключается определением

. Из этой теоремы непосредственно следует, что совокупность всех элементов многообразия

нельзя представить в форме последовательности

, так как в противном случае мы столкнулись бы с противоречием, что некая вещь
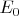
как была бы, так и не была бы элементом многообразия

.
Сформулированная и доказанная здесь теорема соответствует
определению 18 несчётного множества.
Здесь, как видим, также нет доказательства "от противного".



