Дайте рецензию на работу Зенкина

[Someone]

А.А.Зенкин, "Ошибка Георга Кантора". - Вопросы философии, 2000, No. 2, 165-168.
Текст можно найти здесь: http://alexzen.by.ru/papers/vf1/vf-rus.html.
Видимо, это сайт автора. Все цитаты со ссылкой на Зенкина взяты с указанной страницы сайта.
Я перенабрал в цитатах все формулы, заменив символы "О" и "®" в тексте Зенкина общепринятыми символами "$\in$" и "$\Rightarrow$" (видимо, символы "О" и "®" появились из-за неправильного отображения на сайте).
Также я буду ссылаться на две книги (на вторую из них ссылается и Зенкин).

[1]. Георг Кантор. Труды по теории множеств. Москва, "Наука", 1985.
[2]. Стефен К.Клини. Введение в метаматематику. Москва, "Иностранная литература", 1957.

А.А.Зенкин писал(а):

Приведу полный текст этой знаменитой Теоремы Кантора и ее доказательства.
Обозначим через $X$ множество всех действительных чисел, или, что то же, всех точек единичного отрезка $[0,1]$. Введем следующие соглашения. Для простоты мы будем использовать двоичную систему представления действительных чисел. Вместо длинного выражения "действительное число x является элементом множества $X$" будем писать $x\in X$. Исключительно для удобства последующих ссылок будем использовать различные записи, заключенные в фигурные скобки.

Итак, рассмотрим традиционное доказательство Теоремы Кантора (см., например, С.К.Клини, "Введение в метаматематику", М.: ИЛ, 1957, стр. 13).

ТЕОРЕМА КАНТОРА: {Тезис A:} Множество $X$ - несчетно.

ДОКАЗАТЕЛЬСТО КАНТОРА. Допустим противное, т.е. что {допущение метода от противного НЕ-A:} множество $X$ - счетно. Это, по определению, означает, что все его элементы можно занумеровать с помощью обычных конечных натуральных чисел.
Пусть последовательность

$$x_1,x_2,x_3,\ldots,x_n,\ldots,\eqno{(1)}$$

является некоторым таким пересчетом всех $x\in X$, т.е.,
{ B:} для любого $z$, если $z\in X$, то $z$ является элементом последовательности (1), или, короче, $z\in (1)$.
Далее, применяя свой знаменитый диагональный метод к пересчету (1), Г.Кантор строит новое, так называемое "диагональное" действительное число (ДДЧ), скажем, $y_1$ такое, что, по определению, $y_1\in X$, но, по построению, $y_1$ отлично от каждого элемента пересчета (1), т.е. ДДЧ $y_1$ не принадлежит пересчету (1). Следовательно,

{НЕ-B:} данное ДДЧ $y_1\in X$, но это ДДЧ $y_1$ не входит в пересчет (1).

Итак, получено противоречие между НЕ-B and B. Из этого противоречия, с учетом произвольности выбора пересчета (1), Кантор делает свой знаменитый вывод: допущение НЕ-А о счетности множества $X$ - ложно. Следовательно, {A:} множество $X$ - несчетно. Ч.Т.Д.

В первой фразе цитаты Зенкин обещает привести полный текст теоремы Кантора и её доказательства. Однако на самом деле полного текста доказательства нет. Вторая фраза сформулирована, как минимум, неаккуратно, поскольку в ней утверждается, что множество всех действительных чисел совпадает с множеством точек отрезка $[0,1]$.
Выбор двоичной системы счисления допустим, но создаёт некоторые проблемы, и, ввиду отсутствия самой существенной части текста доказательства, не видно, как они преодолеваются. Это очень жаль, так как после процитированного доказательства Зенкин излагает ещё некоторые рассуждения, осмысленность которых зависит от опущенных им деталей.
Далее Зенкин утверждает, что приведённое им доказательство принадлежит самому Кантору, но ссылается почему-то на книгу Клини. На основании этого, видимо, можно предположить, что Клини переписал это доказательство из одной из работ Кантора, а Зенкин процитировал Клини. Позже посмотрим, что написано у Кантора и у Клини.

Как видим, Зенкин настаивает на том, что Кантор доказывает теорему методом "от противного", причём, именно так, как это изложено у Зенкина ("доказательство Кантора"). В этом доказательстве присутствуют 4 "тезиса": {A:}, {НЕ-A:}, {B:}, {НЕ-B:}. Тезис {B:} просто утверждает, что выбранная последовательность действительных чисел включает все действительные числа, то есть, является следствием {НЕ-A:}, а не самостоятельным предположением. Соответственно, когда в результате применения диагонального метода получается утверждение {НЕ-B:}, противоречащее {B:}, по правилам математической логики из него получается {A:}, то есть, утверждение теоремы. Всё ли здесь в порядке?

Заметим, что диагональный метод в стандартном варианте никаким способом не использует тезис {B:}. Этот метод применяется к произвольной последовательности действительных чисел и (если мы об этом позаботились) даёт число, не содержащееся в последовательности. То есть, утверждение {НЕ-B:} получается без какого-либо участия тезисов {B:} или {НЕ-A:}. С таким же успехом мы могли бы начать доказательство фразой "Пусть $x_1,x_2,x_3,\ldots,x_n,\ldots$ - произвольная последовательность действительных чисел." Применив диагональный метод, мы получили бы действительное число, не входящее в эту последовательность, то есть, утверждение {НЕ-B:}, и, сославшись на определение 18, сделали бы вывод о несчётности множества действительных чисел.

Таким образом, доказательства "от противного" по сути здесь нет, есть только некая формальная видимость. Мы можем спокойно сформулировать тезисы {НЕ-A:} и {B:} в любом место доказательства, в том числе, после доказательства утверждения {НЕ-B:}, и заявить о получении противоречия. Разумеется, если сразу после доказательства некоторого утверждения сформулировать противоречащее ему, то получится противоречие (кстати, такие рассуждения встречаются). Зачем, собственно говоря, это понадобилось Зенкину? Да просто иначе ему было бы нечем манипулировать в последующих рассуждениях.

Прежде чем продолжать читать Зенкина, посмотрим на доказательство, изложенное у Клини. Зенкин ссылается именно на это доказательство.

С.К.Клини в [2] писал(а):

Посредством знаменитого "диагонального метода" Кантора было доказано, что в математике рассматриваются и такие бесконечные множества, которые не могут быть пересчитаны. Множество действительных чисел несчетно.
Рассмотрим сначала действительные числа $x$ в полуинтервале $0<x\leqslant 1$. Каждое действительное число из этого полуинтервала однозначно представляется посредством некоторой правильной бесконечной десятичной дроби, т. е. десятичной дроби, первая значащая цифра которой стоит правее запятой и в которой имеется бесконечно много цифр, отличных от $0$. Число может представляться в виде конечной десятичной дроби, т. е. дроби с повторяющимися нулями, но такую дробь можно заменить на бесконечную с повторяющимися девятками. Например, $0{,}483$ или $0{,}483000\ldots$ можно заменить на $0{,}482999\ldots$. Обратно, каждая правильная бесконечная десятичная дробь представляет единственное число из этого полуинтервала.
Допустим теперь, что

$$x_0,x_1,x_2,x_3,\ldots$$

— бесконечный перечень или пересчет некоторых, но не обязательно всех, действительных чисел, принадлежащих этому полуинтервалу. Напишем теперь одну под другой соответствующие им бесконечные десятичные дроби
$\xymatrix{0,&x_{00}\ar[rd]&x_{01}&x_{02}&x_{03}&\ldots\\ 0,&x_{10}&x_{11}\ar[rd]&x_{12}&x_{13}&\ldots\\ 0,&x_{20}&x_{21}&x_{22}\ar[rd]&x_{23}&\ldots\\ 0,&x_{30}&x_{31}&x_{32}&x_{33}\ar[rd]&\ldots\\ \ldots&\ldots&\ldots&\ldots&\ldots&\ldots}$
Образуем диагональную дробь, указанную стрелками. Заменим в ней каждую из последовательных цифр $x_{nn}$ на отличную от нee цифру $x'_{nn}$ так, чтобы при этом не получилась конечная дробь. Например, пусть $x'_{nn}=5$, если $x_{nn}\neq 5$, и $x'_{nn}=6$, если $x_{nn}=5$.
Полученная дробь

$$0{,}x'_{00}x'_{11}x'_{22}x'_{33}\ldots$$

представляет некоторое действительное число $x$, которое принадлежит нашему полуинтервалу, но не входит в рассматриваемый пересчет. Действительно, эта дробь отличается от первой из данных дробей своей первой цифрой после запятой, от второй — своей второй цифрой после запятой, от третьей — третьей цифрой после запятой и т. д.
Поэтому данный пересчет не является пересчетом всех действительных чисел полуинтервала $0<x\leqslant 1$. Пересчета всех действительных чисел этого полуинтервала не существует.

Это классическое доказательство несчётности множества действительных чисел диагональным методом. Никаких намёков на доказательство "от противного" здесь нет, более того, Клини подчёркивает, что рассматривается "бесконечный перечень или пересчет некоторых, но не обязательно всех, действительных чисел, принадлежащих этому полуинтервалу". Термин "перечень" или "пересчёт" у Клини предполагает, что все члены последовательности $x_0,x_1,x_2,x_3,\ldots$ попарно различны, поэтому заключительное утверждение доказательства Клини соответствует определению 19.
Как понимать тогда слова Зенкина: «рассмотрим традиционное доказательство Теоремы Кантора (см., например, С.К.Клини, "Введение в метаматематику", М.: ИЛ, 1957, стр. 13)»?

А.А.Зенкин писал(а):

К сожалению, знаменитый диагональный метод Кантора не учитывает и не использует количественных характеристик (т.е. мощности) тех множеств, к которым он применяется (см. [1,2,4]). Поэтому в рассматриваемом случае Кантор, для получения вожделенного противоречия, использует только актуальность пересчета (1), т.е. условие, что пересчет (1) "содержит все $x\in X$ ".

Ну, как мы видели, диагональный метод не нуждается в этом условии, и, более того, Клини, на которого ссылается Зенкин, на это явным образом указывает. Так что здесь Зенкин просто умышленно врёт (прошу прощения за непарламентские выражения). Потом мы увидим, что и сам Кантор без этого условия прекрасно обходится и также не получает никакого "вожделенного противоречия".

А.А.Зенкин писал(а):

Тривиально очевидно, что для пересчета (1) в двоичной системе можно построить только единственное ДДЧ $y_1$.

Это, извините, смотря как строить. Легко можно построить и больше.

А.А.Зенкин писал(а):

С другой стороны, согласно канторовскому определению понятия бесконечного множества, мощность последнего не изменится, если к нему добавить … один новый элемент.
Поэтому мы можем добавить ДДЧ $y_1$ к исходному счетно-бесконечному пересчету (1), например, таким образом:

$$y_1,x_1,x_2,x_3,\ldots,x_n,\ldots.\eqno{(1.1)}$$

Очевидно, что теперь новый счетно-бесконечный пересчет (1.1) будет содержать все действительные числа множества $X$ , т.е.

{B:} для любого $z$, если $z\in X$, то $z\in(1.1)$.

А это, извините, уже совсем глупо. Если какой-то метод даёт единственный элемент множества, то ниоткуда не следует, что там нет других элементов. Поэтому никакого {B:} не получается.
Поэтому на этом месте бесконечная цепочка рассуждений Зенкина

А.А.Зенкин писал(а):

$$\text{НЕ-A}\Rightarrow\text{B}\Rightarrow\text{НЕ-B}\Rightarrow\text{B}\Rightarrow\text{НЕ-B}\Rightarrow\text{B}\Rightarrow\text{НЕ-B}\Rightarrow\text{B}\Rightarrow\ldots\eqno{(2)}$$

обрывается, едва начавшись - на первом же {НЕ-B:}. Поэтому последующие его выводы оказываются ни на чём не основанными, высосанными из пальца.

Есть ещё продолжение этого рассуждения для случая, когда используется не двоичная система счисления.

А.А.Зенкин писал(а):

Очевидно, что если мы возьмем не двоичную, а любую другую систему счисления с основанием больше 2, то для любого данного счетного пересчета (1) Кантор сможет построить уже не единственное ДДЧ, а бесконечное множество ДДЧ, скажем, множество $Y$.

Здесь Зенкин рассматривает два случая: когда $Y$ счётно и когда $Y$ несчётно. Второй случай он отвергает на том основании, что его "требуется доказать", не замечая, что точно так же "требуется доказать" и первый случай. Правда, все эти рассуждения убиваются тем обстоятельством, что если диагональный метод даёт некоторое множество $Y$ действительных чисел, не содержащихся в заданной последовательности, то ниоткуда не следует, что множество $Y$ содержит все такие числа. А также изначальной никчёмностью этих рассуждений, поскольку доказательство теоремы Кантора закончилось в тот момент, когда было построено число (одно!), не содержащееся в произвольно взятой последовательности - согласно определению несчётного множества.

Доказательство несчётности множества действительных чисел у Кантора встречается два раза: в статьях "Об одном свойстве совокупности всех действительных алгебраических чисел" (стр. 20 - 21) и "О бесконечных линейных точечных многообразиях" (стр. 43 - 45). Я приведу первое из них, поскольку оно намного короче. Третий раз (в статье "Об одном элементарном вопросе учения о многообразиях", стр. 170 - 171) Кантор пишет, что эту теорему можно доказать значительно проще, после чего рассматривает применение диагонального метода для доказательства несчётности множества двоичных последовательностей и обобщение этого метода на функции, определённые на произвольном множестве и принимающие два различных значения. Как отсюда вывести теорему о несчётности множества действительных чисел, Кантор не объясняет, но все необходимые для этого утверждения в предшествующих работах Кантора доказаны.

Г.Кантор в [1] писал(а):

Если по какому-нибудь закону задана бесконечная последовательность отличных друг от друга числовых величин

$$\omega_1,\omega_2,\ldots,\omega_{\nu},\ldots,\eqno{(4)}$$

то во всяком заданном интервале $(\alpha\ldots\beta)$ можно определить число $\eta$ (а значит, и бесконечно много таких чисел), которое не содержится в последовательности (4). Это и предстоит теперь доказать.
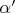
Мы начинаем с произвольно заданного интервала $(\alpha\ldots\beta)$, и пусть $\alpha<\beta$. Два первых числа последовательности (4), которые расположены в этом интервале (за исключением концов), можно обозначить через $\alpha'$, $\beta'$, и пусть $\alpha'<\beta'$; аналогично два первых числа нашей последовательности, расположенных внутри $(\alpha'\ldots\beta')$, обозначим через $\alpha''$, $\beta''$, и пусть $\alpha''<\beta''$; по тому же закону образуем следующий интервал $(\alpha'''\ldots\beta''')$ и т. д. Здесь, следовательно, $\alpha',\alpha'',\ldots$ по самому определению являются определенными числами нашей последовательности (4), индексы которых все время возрастают; то же самое справедливо для чисел $\beta',\beta'',\ldots$. Примем, далее, числа $\alpha',\alpha'',\ldots$ возрастающими по величине, а числа $\beta',\beta'',\ldots$ убывающими по величине. Каждый из интервалов $(\alpha\ldots\beta),(\alpha'\ldots\beta'),(\alpha''\ldots\beta''),\ldots$ содержит в себе все следующие за ним. Теперь мыслимы только два случая.
Или число построенных таким образом интервалов конечно, и пусть последний из них будет $(\alpha^{(\nu)}\ldots\beta^{(\nu)})$. Так как внутри него может быть расположено самое большее одно число последовательности (4), то в этом интервале можно взять число, не содержащееся в последовательности (4), и тем самым для этого случая теорема доказана.
Или число построенных интервалов бесконечно. Тогда числа $\alpha',\alpha'',\ldots$, поскольку они возрастают по величине, не возрастая до бесконечности, имеют определенный предел $\alpha^{\infty}$; то же самое верно для чисел $\beta',\beta'',\ldots$, так как они убывают по величине, и пусть их предел $\beta^{\infty}$.
Если $\alpha^{\infty}=\beta^{\infty}$ (случай, имеющий место для совокупности $(\omega)$ всех действительных алгебраических чисел), то легко убедиться, обратившись к определению интервала, что число $\eta=\alpha^{\infty}=\beta^{\infty}$ не может содержаться в нашей последовательности. Если же $\alpha^{\infty}<\beta^{\infty}$, то всякое число $\eta$ внутри интервала $(\alpha^{\infty}\ldots\beta^{\infty})$ или на его границе удовлетворяет выставленному требованию не содержаться в последовательности (4).

Здесь нет ни доказательства "от противного", столь красочно расписанного Зенкиным, ни диагонального метода. Кантор строит действительное число, не содержащееся в произвольно заданной последовательности попарно различных действительных чисел, используя свойства множества действительных чисел, известные из курса математического анализа. Утверждение теоремы, таким образом, соответствует определению 19 несчётного множества.
Я не буду приводить второго доказательства Кантора, поскольку оно существенно длиннее, но по сути мало отличается от процитированного. Желающие могут взять сборник работ Кантора и убедиться, что там тоже нет ни доказательства "от противного", ни диагонального метода.

А вот диагональный метод (стр. 170 - 171).

Г.Кантор в [1] писал(а):

... если $m$ и $w$ — два каких-либо исключающих друг друга признака (Charaktere), то рассматриваем совокупность $M$ элементов

$$E=(x_1,x_2,\ldots,x_{\nu},\ldots),$$

зависящих от бесконечно многих координат $x_1,x_2,\ldots,x_{\nu},\ldots$, где каждая из этих координат есть $m$ или $w$. Пусть $M$ — совокупность всех элементов $E$.
Элементами совокупности М являются, например, три следующие:

$$E^{\mathrm{I}}=(m,m,m,m,\ldots),$$

$$E^{\mathrm{II}}=(w,w,w,w,\ldots),$$

$$E^{\mathrm{III}}=(m,w,m,w,\ldots).$$

Теперь я утверждаю, что такое многообразие $M$ не имеет мощности последовательности $1,2,\ldots,\nu,\ldots$.
Это вытекает из следующей теоремы:
«Если $E_1,E_2,\ldots,E_{\nu},\ldots$ — какая-либо просто бесконечная последовательность элементов многообразия $M$, то всегда существует такой элемент $E_0$ многообразия $M$, который не совпадает ни с каким $E_{\nu}$».
Пусть

$$E_1=(a_{1,1},a_{1,2},\ldots,a_{1,\nu},\ldots),$$

$$E_2=(a_{2,1},a_{2,2},\ldots,a_{2,\nu},\ldots),$$

$$.\qquad.\qquad.\qquad.\qquad.\qquad.$$

$$E_{\mu}=(a_{\mu,1},a_{\mu,2},\ldots,a_{\mu,\nu},\ldots),$$

$$.\qquad.\qquad.\qquad.\qquad.\qquad.$$

Здесь $a_{\mu,\nu}$ суть определенно $m$ или $w$. Определим теперь последовательность $b_1,b_2,\ldots,b_{\nu},\ldots$ так, чтобы $b_{\nu}$ был тоже равен только $m$ или $w$ и отличен от $a_{\nu,\nu}$.
Итак, если $a_{\nu,\nu}=m$, то $b_{\nu}=w$, а если $a_{\nu,\nu}=w$, то $b_{\nu}=m$.
Если теперь мы рассмотрим элемент

$$E_0=(b_1,b_2,b_3,\ldots)$$

многообразия $M$, то очевидно, что равенство

$$E_0=E_{\mu}$$

не может иметь места ни для какого положительного целочисленного значения $\mu$, так как в противном случае для соответствующего $\mu$ и для всех целочисленных значений $\nu$ было бы

$$b_{\nu}=a_{\mu,\nu},$$

а значит, в частности,

$$b_{\mu}=a_{\mu,\mu},$$

что исключается определением $b_{\nu}$. Из этой теоремы непосредственно следует, что совокупность всех элементов многообразия $M$ нельзя представить в форме последовательности $E_1,E_2,\ldots,E_{\nu},\ldots$ , так как в противном случае мы столкнулись бы с противоречием, что некая вещь $E_0$ как была бы, так и не была бы элементом многообразия $M$.

Сформулированная и доказанная здесь теорема соответствует определению 18 несчётного множества.
Здесь, как видим, также нет доказательства "от противного".

[Виктор Викторов]

Виктор Викторов в сообщении #408466 писал(а):

migmit в сообщении #408464 писал(а):

Просто для математиков вопросы "потенциальной" и "актуальной" бесконечностей - давно пройденный этап.

Ссылочку бы мне...

Someone в сообщении #408552 писал(а):

Ну какую Вам "ссылочку", если термины "потенциальная бесконечность" и "актуальная бесконечность" в современной математике не употребляются. Они употребляются исключительно в околоматематических философствованиях.

Вот мой источник знаний о потенциальной и актуальной бесконечностях:

«As a rule, in 19th century mathematics, infinity appears only in its “potential” form. <…> Potential infinity can be illustrated by a very simple example: the expression $\lim\limits_{n \to \infty}(\frac1{n})=0$ <…> is nothing more than an abbreviation of the statement “the quotient $\frac1{n}$ can be made to approach $0$ with any desired accuracy if positive integer $n$ is chosen sufficiently large.” <…>
On the other hand, the problem of infinity as an “actual” absolute magnitude was raised at an early stage of Catholic theology and philosophy, in particular by Augustinus and Thomas Aquinas and his school. <…> … it was really Georg Cantor, the creator of Mengenlehre (set theory), who between 1873 and 1897 carefully laid the foundations of the theory of actual infinity, introduced it systematically into mathematics (and philosophy), developed around it a new branch of mathematics, the theory of sets.» Abraham A. Fraenkel “Set Theory and Logic” ADDISON-WESLEY PUBLISHING COMPANY, INC. 1966 Стр. 1-2.

Перевод: «Как правило, в математике 19го века бесконечность появляется только в «потенциальной» форме. <…> Потенциальная бесконечность может быть иллюстрирована очень простым примером: выражение $\lim\limits_{n \to \infty}(\frac1{n})=0$ не более чем аббревиатура выражения «дробь $\frac1{n}$ может быть приближена к $0$ с любой желаемой точностью, если положительное целое $n$ выбрано достаточно большим.» <…>
С другой стороны, проблема бесконечности как «актуальной» абсолютной величины была поднята в раннем периоде католической теологии и философии, в частности Августином и Фомой Аквинским и его школой. <…> … на самом деле это был Георг Кантор, творец Mengenlehre (теории множеств), кто между 1873 и 1897 [годами] тщательно заложил основания теории актуальной бесконечности, систематически представил её в математике (и философии) и развил вокруг неё новую ветвь математики, теорию множеств.» Абрахам Френкель «Теория множеств и логика» 1966 год. Стр 1-2.

[aku]

Someone в сообщении #414177 писал(а):

Если $\alpha^{\infty}=\beta^{\infty}$ (случай, имеющий место для совокупности $(\omega)$ всех действительных алгебраических чисел), то легко убедиться, обратившись к определению интервала, что число $\eta=\alpha^{\infty}=\beta^{\infty}$ не может содержаться в нашей последовательности.

Прошу прощения, не очень понятно, если $\eta=\alpha^{\infty}=\beta^{\infty}$, то $\eta - это точка, значит, она содержится в нашей последовательности. Да и внутри точки не может содержаться никакого интервала.

-- 10.10.2011, 22:54 --

Someone в сообщении #414177 писал(а):

Здесь нет ни доказательства "от противного", столь красочно расписанного Зенкиным, ни диагонального метода. Кантор строит действительное число, не содержащееся в произвольно заданной последовательности попарно различных действительных чисел, используя свойства множества действительных чисел, известные из курса математического анализа. Утверждение теоремы, таким образом, соответствует определению 19 несчётного множества.

И еще одна непонятка. Какое это чудное прямое доказательство, вместо сомнительного косвенного "диагонального". Так почему же все эти Хаусдорфы, Френкели, Клини, Клайны с Бурбаками..., Менделеевы с Крузенштернами оперируют в своих трудах только этой убогой диагональной косностью? Они чо, безграмотные?

[Someone]

Нехорошо, что Вы приписываете мне то, что писал не я, а Кантор.

aku в сообщении #491460 писал(а):

Прошу прощения, не очень понятно, если $\eta=\alpha^{\infty}=\beta^{\infty}$, то $\eta - это точка, значит, она содержится в нашей последовательности.

??? Предъявите доказательство. Вовсе не всякая "точка" содержится в заданной последовательности.

aku в сообщении #491460 писал(а):

Да и внутри точки не может содержаться никакого интервала.

Кто утверждал, что он там содержится?

aku в сообщении #491460 писал(а):

Какое это чудное прямое доказательство, вместо сомнительного косвенного "диагонального".

Почему "прямое" и почему "косвенное"? Они устроены одинаково: если задана некоторая последовательность действительных чисел, то немедленно предъявляется действительное число, не содержащееся в этой последовательности. Совершенно "прямо", хотя и разными способами.

aku в сообщении #491460 писал(а):

Так почему же все эти Хаусдорфы, Френкели, Клини, Клайны с Бурбаками..., Менделеевы с Крузенштернами оперируют в своих трудах только этой убогой диагональной косностью? Они чо, безграмотные?

Предъявите доказательство, что перечисленные Вами лица не знали этого "чудного прямого" доказательства.

Что касается "чудности" и "убогости", то Вы совершенно не правы. "Убогий" диагональный метод является универсальным, в то время как "чудный" метод работает только в весьма специальных случаях.

-- Вт окт 11, 2011 03:19:34 --

Виктор Викторов в сообщении #429789 писал(а):

Перевод: «Как правило, в математике 19го века бесконечность появляется только в «потенциальной» форме. <…> Потенциальная бесконечность может быть иллюстрирована очень простым примером: выражение $\lim\limits_{n \to \infty}(\frac1{n})=0$ не более чем аббревиатура выражения «дробь $\frac1{n}$ может быть приближена к $0$ с любой желаемой точностью, если положительное целое $n$ выбрано достаточно большим.» <…>
С другой стороны, проблема бесконечности как «актуальной» абсолютной величины была поднята в раннем периоде католической теологии и философии, в частности Августином и Фомой Аквинским и его школой. <…> … на самом деле это был Георг Кантор, творец Mengenlehre (теории множеств), кто между 1873 и 1897 [годами] тщательно заложил основания теории актуальной бесконечности, систематически представил её в математике (и философии) и развил вокруг неё новую ветвь математики, теорию множеств.» Абрахам Френкель «Теория множеств и логика» 1966 год. Стр 1-2.

Здесь ведь нет математических определений потенциальной и актуальной бесконечности, так что это опять околоматематические философствования, и не более того. Я уже не говорю о том, что примеры приводятся совершенно несравнимые - предел и множество.

[aku]

Большое-пребольшое спасибо г-н Someone, сэр! А я же по своей инфантильности полагал, что эта тема за 7 месяцев молчания совсем уже умерла. Поэтому и попытался реанимировать поврежденный нерв, как полагается, сразу напряжением 500 вольт. Виноват, был не прав, вспылил, раскаиваюсь - поскольку здесь, оказывается, действуют дополнительные нервные связи. У меня давно имеется ряд соображений по обсуждаемым темам. Но нужно осмотреться, время для неторопливого сосредоточения, накопления кэньсё и т.п., в чем я Вам искренне завидую - а то здесь ведь так сильно бьют за плохое знание матчасти!. Надеюсь на Ваше конструктивное оппонирование в будущем.
Надеюсь также, что модераторы на первый раз не накажут меня очень больно за это не относящееся к теме сообщение?
Клянусь своей никчемной жизнью, что никогда-никогда более себе подобного отступления от Правил не позволю!
P.S. Кроме того, даже и этим сообщением я, наверное, увеличиваю свой рейтинг, понятно ведь и уроду, что первую тысячу лет трудновато, а потом привыкаешь, поэтому когда-нибудь, может быть, дослужусь и до 6 звездочек, а то до сих пор на моих синих погонах в шкафу нет даже и одной лычки.

[bot]

(Оффтоп)

aku в сообщении #491653 писал(а):

когда-нибудь, может быть, дослужусь и до 6 звездочек

Непременно, я даже знаю, когда - это произойдёт 05/10/17.

[aku]

Дорогие заслуженные коллеги! Вот в этой теме вы много раз выступали, например:

Dialectic в сообщении #408353 писал(а):

Друзья, дайте пожалуйста рецензию на работу А.А.Зенкина

Виктор Викторов в сообщении #408458 писал(а):

Я пишу роман под названием «Моя жизнь без А.А.Зенкина».

migmit в сообщении #408464 писал(а):

Просто для математиков вопросы "потенциальной" и "актуальной" бесконечностей - давно пройденный этап.

epros в сообщении #408527 писал(а):

"Потенциальная" может подразумевать "теоретически допустимая", но такая, действительное существование ("актуальность") которой мы не берёмся утверждать.

Someone в сообщении #408552 писал(а):

Приведите, пожалуйста, эту аксиому. Сформулируйте её так, как формулируются другие аксиомы теории множеств. Например, аксиома регулярности

В.О. в сообщении #409429 писал(а):

Если Вы пытаетесь пересчитать все числа на (0,1), то попытка не удалась.

Xaositect в сообщении #410176 писал(а):

А бесконечные последовательности в каком порядке идут?

и это очень для меня радостно.

Тем не менее, видимо, по несчастью мне повезло с первого входа наткнуться на столь глубоко и широко обсуждаемую дискуссионную тему. Однако крайне большой объем и разнородность представленного материала может создать определенные затруднения у будущих поколений читателей, исследователей интернет-культуры XXI века и историков науки. Поэтому кому-то, видимо, необходимо взять на себя неблагодарный труд по структурированию этих текстов, хотя бы в виде некого краткого конспективного оглавления, чтобы весь представленный необъятный информационный поток перестал напоминать неоконченную пьесу для механического пианино.

Очень и очень надеюсь, что нижепреведенные конспекты будут восприняты уважаемой публикой, как совершенно, ну совершенно непредвзятый неофилический взгляд абсолютно, ну абсолютно внешнего и абсолютно случайного наблюдателя. Итак:

Прелюдия: 02.02.2011, 21:33 - 03.02.2011, 02:36 (длительность 5 часов, 7 сообщений)
Dialectic (заслуженый инициатор темы) вдруг наткнулся на работу Зенкина и просит у коллег пояснений. Участники Ales, shwedka, Xaositect и Dialectic обмениваются репликами, неизвестными друг-другу ссылками на др.источники (Шмарко, Френкель) и благодарят друг друга.

Занос №1: 02.02.2011, 23:14 - 05.02.2011, 02:32 (3 суток, 25 сообщений)
Вдруг Migmit возмутился термином «актуальная бескрнечность» у Зенкина. Начинается долгая дискуссия о его соотношении с потенциальной бесконечночтью, General Set Theory, аксиомой бесконечности, аксиоматиками ZFC и CRA и др. Участвуют Migmit, Виктор Викторов, epros, Someone, master с последующей аргументацией на языке формальной логики. Актеры Прелюдии и проблемы Зенкина полностью исчезают со сцены (некоторые навсегда).

Супер-занос №2: 05.02.2011, 11:30 - 12.02.2011, 23:56 (7.5 суток, 65 сообщений)
Внезапно возникает новичок tatle11be с новым методом пересчета действительных чисел. В дискуссионную атаку сразу бросаются уже другие специалисты: Андрей АK, Xaositect, В.О., bot, затем последовательно присоединяются: migmit, epros, Someone, ewert, временно замолкает tatle11be, его адвокатирует в диагональном методе Андрей АK, переходя затем к своему двоичному представлению и упорядочиванию действительных и натуральных чисел ( ранее опробованному в теме «Замкнутая бесконечность»). Все критикуют Андрея АK и друг друга. Снова активно вступает tatle11be. Вмешивается модератор Jnrty 11.02.2011, 03:14, указывая на ошибки и некорректности с попыткой вернуться к обсуждению Зенкина. Дискуссия принимает агрессивный характер с обвинениями Зенкина во вранье и критикой новых заявлений tatle11be. Андрей АK окончательно устает от критики в свой адрес и исчезает со сцены. В общем, научные мысли отчаянно бьются друг о друга и в тесных оковах Разума в поисках мифического консенсуса (куда смотрят модераторы!?).

Прорыв №1. 15.02.2011, 22:14 (5 сообщений). Для упорядочивания дискусии Someone формулирует 19 формальных логических правил и 2 теоремы, он обсуждает с Migmit и корректирует эти тезисы, но более никто этими тезисами не интересуется! - интересно, почему, не правда ли? Но тут внезапно возникает неофил Tod Leben с вопросом о потроении диагонали Кантора на цепочках яблок – модератор Jnrty резко это купирует за невежество

Прорыв №2. 18.02.2011, 00:29 (1 сообщение). Someone наконец-то внимательно изучает работу Зенкина "Ошибка Георга Кантора", цитирует ее фрагмент и производит ее детальную и агрессивную критику с подробными цитатами из работ Кантора и Клини, обвинениями в высасывании из пальца, умышленном вранье (в частности показано, что вообще не нужно ни доказательства "от противного", ни диагонального метода) – НАКОНЕЦ-ТО мы вернулись к исходной теме!!! Но Виктор Викторов 01.04.2011, 06:51 все это игнорирует и пытается вернуться к проблематике актуальной и потенциальной бесконечности, требуя от аудитории какуе-то ссылочку на давно уже пройденное и забытое. Никто ссылочку ему не дает. На этом вся эта длительная дискуссия ОБО ВСЕМ чудесным образом и счастливо умирает.
Возникает закономерный вопрос: 1) или прорывы 1,2 совершенно не устраивают остальных учасников своей строгостью, конкретностью и формализмом; 2) или же они настолько проясняют ситуацию, что более обсуждать что-либо становится бессмысленным?

Через 7 месяцев после клинической смерти дискуссии человеком из Ниоткуда выплывает ваш покорный слуга, задавая 2 вопроса по последним изысканиям Someone, и очень быстро получает очень и очень вразумительный ответ с корректировкой одного из заявлений Прорыва №2.

Занавес падает... Все встают и бегут в гардероб за шляпами...

P.S.
1) в вышеприведенном конспекте автор никоим образом не предполагает посягнуть на священную свободу форумной научной общественности выбирать направления дальнейших дискуссионных разветвлений, как бы далеко они не заводили умы несчастных читателей от изначальной темы;
2) с другой стороны, наблюдённая политкорректность высказываний данного форума (за редкими отмеченными исключениями) разительно контрастирует с необузданной эмоциональностью других форумов по данной же тематике (поищите сами);
3) видимо, в данном форуме есть еще много тем, требующих подобного коспектирования, поэтому, надеюсь, что кто-нибудь когда-нибудь еще последует данному примеру и среди новороссийскх руд, хранящих гордое терпенье, не пропадет мой скромный труд, ... пойдет на удобренье!

Искренне Ваш Навеки,
случайный прохожий АПК

Jnrty:

Предупреждение за злостный offtopic.

[aku]

Александр Александрович Зенкин, доктор физико- математических наук, профессор, ведущий научный сотрудник Отдела Интеллектуальных прикладных систем Вычислительного Центра РАН, член Российской Ассоциации Искусственного Интеллекта и Философского Общества России, член Международной федерации Художников и Творческого Союза Художников России. А.А. Зенкин закончил МГУ и получил два высших образования – в области химии и математики. Ученую степень доктора физико-математических наук Александр Александрович получил за работы по теории чисел, направление, которым он активно занимался большую часть своей долгой научной жизни. Его основные научные результаты в этом направлении были связаны с обобщением известной теоремы Гильберта из теории чисел, которое обеспечило полное решение классической проблемы Варинга. Он автор более 200 научных работ, опубликованных в самых престижных отечественных и зарубежных изданиях.

Одной из многочисленных заслуг А.А. Зенкина является инициация интереса отечественных логиков и философов к критике теории множеств, поскольку таковая практически отсутствовала в СССР в до- и послевоенное время. Отечественные исследователи ограничивались обычно пересказом критики зарубежных авторитетов преимущественно начала 20-го века (о математиках, за редким исключением, разговор отдельный). Благодаря своей энергии и авторитету им по этой теме было опубликовано более двух десятков работ (значительная часть на английском, многие ли из вас могут аналогичным похвастаться?), включая Вопросы философии (3) и газетную публицистику. И именно последнее вызвало серьезный резонанс в обществе, благодаря которому и вы обсуждаете сейчас подобные проблемы на многочисленных форумах. Поэтому вы должны быть благодарны за это заслуженному и авторитетному ученому, а не покидать сразу же инициированную вами же дискуссию, быстро получив что-то, похожее на рецензию, не увлекаться длительными заносящими отступлениями, или же вдруг случайно пролистав одну из его 200 работ, позволять себе вольности в его адрес, включая и прямые оскорбления, пользуясь тем, что он не может вызвать вас к барьеру (как же мне стыдно за подобное, господа!).

Несомненные заслуги А.А. Зенкина в критике теории множеств могу в последствие конспективно перечислить, если участники еще сохранили интерес к этой неисчерпаемой теме.

[Jnrty]

aku в сообщении #496586 писал(а):

позволять себе вольности в его адрес, включая и прямые оскорбления, пользуясь тем, что он не может вызвать вас к барьеру (как же мне стыдно за подобное, господа!)

Возьмите обсуждаемую работу Зенкина, книгу Клини и сборник работ Кантора и сравните то, что написано у Клини и Кантора, с тем, что приписывает им Зенкин. А потом будем обсуждать, за кого Вам должно быть стыдно.

Извините, но нас не интересует критика математических теорий со стороны человека, весьма слабо разбирающегося в критикуемых теориях и перевирающего те рассуждения, которые он критикует.

Jnrty:

Посему тему закрываю.