Теперь предлагаю рассмотреть другой ряд, а именно, последовательный ряд чисел

.
Если провести проверку делимости данных чисел на последовательные простые числа, то получим следующий рисунок:

Рис. 2
Чтобы описать то, что видно на рисунке, введем определения:
Число

назовем "взаимнопростым", если

взаимнопростое по отношению к примориалу

, где

- натуральное число.
Число

назовем "простым", если

взаимнопростое по отношению к примориалу

, где

- наибольшее простое число, непревосходящее
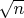
.
Число, не являющееся "простым", назовем "составным".
Цветовые обозначения на рис. 2 такие же, что и на рис. 1 (естественно, с учетом кавычек).
Из рис. 2 видно, что каждое "простое" число соответствуют паре простых-близнецов. Действительно, если числа

и

- простые, то их произведение

будет взаимнопростым по отношению ко всем простым, непревосходящим
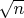
.
Введем еще одно понятие:
Количество чисел

, не больших натурального числа

и "взаимнопростых" с ним, назовем "функцией Эйлера"

.
Для простых

"функция Эйлера" равна:

, т.к. числа, имеющие остаток

, и только эти числа могут иметь остаток

. Исключение составляет простое

. Для него

.
"Функция Эйлера" мультипликативна, т.е.

.
Следовательно, используя "функции Эйлера", можно рассчитать количество чисел, на интервале от

до

"взаимнопростых" с этим примориалом:

Тогда среднее количество чисел

, "взаимнопростых" с примориалом

и расположенных на интервалах длиной

, равно:

.
(чтобы избежать недоразумений, обращаю внимание на индексы).
После сокращения чисел в числителе и знаменателе, получим выражение, как произведение дробей:

, каждая из которых за исключением первой больше единицы. Т.к. число простых чисел бесконечно, то бесконечно и число таких дробей. Следовательно,

стремится к бесконечности.
На интервалах длиной

на участке от

до

все числа, "взаимнопростые" с примориалом

, являются "простыми". Количество таких интервалов с каждым простым

увеличивается и также стремится к бесконечности.
Таким образом, показано, что число пар простых-близнецов бесконечно.
p.s. Интересно то, что пары простых-близнецов сами являются своеобразным "тормозом" роста значения

.