В первом сообщении, по крайней мере, было:
Из следующих 4-х последовательностей одна была получена подбрасыванием монетки 50 раз (0 соответствует орлу, а 1 - решке), а остальные — придуманы мной.
1) 00000000000000000000000000000000000000000000000000
2) 00000000000000000000000001111111111111111111111111
3) 00111100000100110100000111010111101000111101011010
4) 01010101010101010101010101010101010101010101010101
Как вы думаете, какая из последовательностей, скорее всего, была получена подбрасыванием монетки? Почему? Какова вероятность того, что это 1-ая последовательность? 2-ая? 3-я? 4-я?
Нетрудно видеть, что априори каждая из этих последовательностей могла получиться в результате
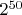
бросаний монеты с вероятностью

. Поэтому, казалось бы, нет причин предпочесть одну из них остальным. Однако, многие люди имеют стойкое ощущение, что именно последовательность 3 получена подбрасыванием монетки, так как является более "случайной", и даже приводят вычисления в поддержку этого взгляда. Какой же взгляд является правильным?
у меня страница сохранённая осталась...
Добавлено спустя 12 минут 37 секунд:Почему - я указал
А вот можно ли как-то учесть, что в приведённом примере три случая "похожи" друг на друга, и отсюда с некоторой вероятностью вывести критерий "красивости"? Тогда, чем больше примеров приведено, тем с большей уверенностью мы можем судить о критерии "красивости", используемой автором... Эта вероятность, что мы не угадали критерий, конечно, уменьшает мою оценку...

Хотя, я только что заметил сообщение
STilda, оно гораздо более в тему, чем моё...
Тут идет некоторая игра точек отсчета. Две точки отсчета.
Первая: дана ОДНА последовательность, с какой вероятностью мы ее получим? ответ такой, что 1),2),3),4) - имеют одинаковую вероятность.
Вторая: Имеем НАБОР последовательностей. Тут внимание незаметно для нас переносится на "какая вероятность получить последовательность со свойством Х".
Тоесть, если НАБОР последовательностей, то важна вероятность обнаружить у последовательности свойство Х.
Свойств можно придумать очень много. Когдато занимался вопросом оценки качества генератора случайных последовательностей. Есть стандарты, в одном из них 16 различных свойств, по которым проверяется случайность.
Примеры свойств:
Например, делаем серию подкидываний монетки по N раз.
1. Какова вероятность такой последовательности, что в ней |количество нулей - количество единиц| > N/3.?
2. Какова вероятность того, что будут все нули?
3. Какова вероятность того, что нулей и единиц поровну?
4. Какова вероятность того, что длина повторяющегося шаблона равна 2? (как в последовательности 4)
5. Какова вероятность того, что в последовательности будет непрерывная серия из M единиц?
Ну и так далее...
С этой точки зрения наиболее правдоподобной является последовательность 3).



