Всё основное уже пояснено. В той геометрии Минковского, которая реально применяется в имеющих реальный физический смысл задачах, векторам не сопоставляются комплексные числа.
Квадрат интервала

это действительное число, а не комплексное.
(Разумеется, как и всякое действительное число его можно считать комплексным, но тогда аргумент у него тривиальный, не представляющий какого-то особого интереса: либо это

если

, либо

если

Если

то аргумент неопределённый.)
Важный геометрический смысл в геометрии Минковского имеют и находят применение в задачах действительные величины:

либо

либо

и действительные положительные корни квадратные из них.
На всякий случай вот две схемки, поясняющие структуру пространства Минковского, т.е. поясняющие "правила соответствия" между векторами-отрезками в пространстве Минковского и их длинами

либо

Важным является не представление интервала на какой-то совершенно не нужной здесь комплексной плоскости, а наклон (или направление) отрезков по отношению к координатным осям

и

на такой карте пространства Минковского:
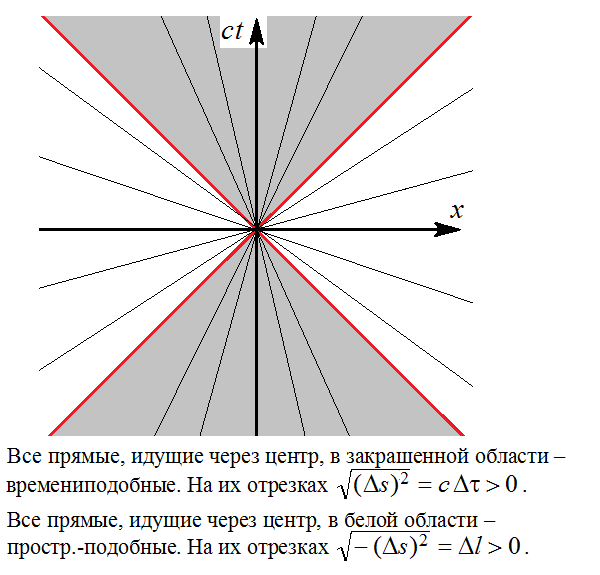
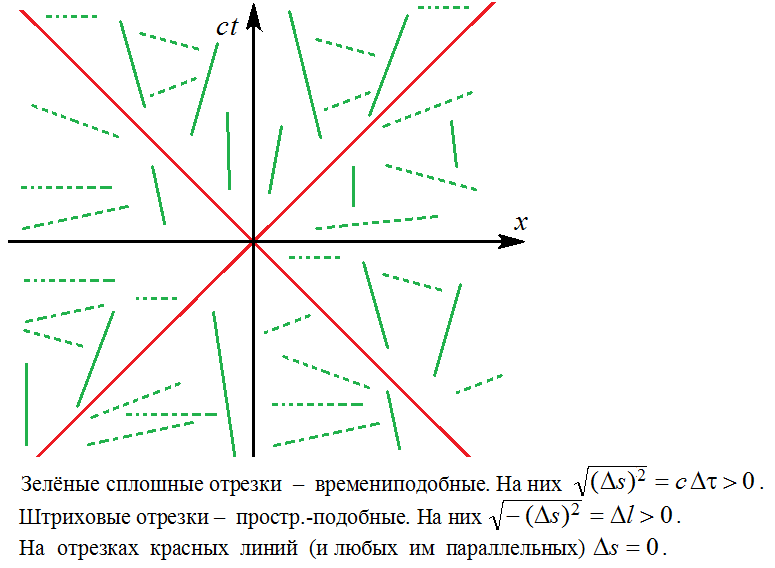
Более содержательными были бы картинки с изображениями световых конусов в различных точках пространства Минковского, с мировыми линиями по-всякому движущихся тел, и, главное, - относящиеся к разным системам координат. Но до самого-то главного, - до изучения преобразований координат, - топикстартер по-видимому ещё не добрался.
P.S. В литературе по физике нет словесных
строгих определений. Смысл и способы применения физических величин определяются не столько их названиями, сколько уравнениями в конкретных задачах. Притом задачи формулируются в связи с экспериментами, а не на основе лишь абстрактных аксиом. Поэтому Ландау и Лифшиц, да и авторы других книг, называют

и интервалом, и "расстоянием с формальной математической точки зрения", а также, в соответствующих задачах, - собственным временем или собственной длиной. (Т.е. слово "расстояние" там не выступает в роли строгого термина. Как говорится: хоть горшком назовите, но только в печь не ставьте.)
P.P.S. У меня сложилось впечатление, что топикстартер желает настаивать на своих представлениях, вместо того чтобы разумным образом понять написанное в учебниках и в уже многочисленных форумных ответах. Не вижу, что ещё тут пояснять, ухожу из этой ветки.



