mathematician123, спасибо, это похоже на то, что я спрашивал. Вторая группа имеет такую решётку подгрупп:
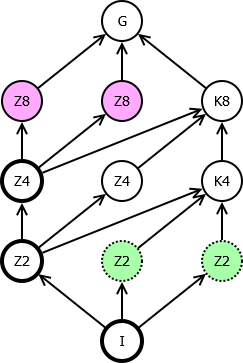
Цветом выделены орбиты относительно группы автоморфизмов. Белый фон имеют характеристические подгруппы. Жирная граница обозначает центральные подгруппы, штрихованные — не являющиеся нормальными. K4 означает группу

, а K8 —

.
Первая абелева группа имеет такую решётку:
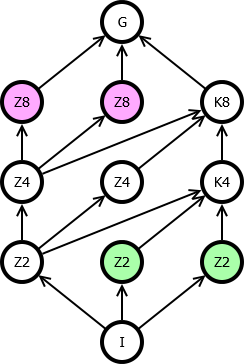
Все подгруппы, разумеется, центральные и нормальные. Но это единственное отличие, даже фактор группы для общих нормальных подгрупп совпадают (там не много, что может получиться). В частности, две подгруппы

отличаются не только тем, подгруппами каких других подгрупп они являются, но и своими фактор-группами:

для левой и

для правой. И это одинаково для обеих групп.
Интереснее, конечно, было бы найти (если они существуют) две не абелевы группы с одинаковой решёткой и подгруппами с одинаковыми свойствами. У меня есть подозрение, что центральность и нормальность всегда будут дифференцирующими характеристиками. Иначе, что толку от классификации групп?
В одной книге есть такой пример:
А что за книга (автор, название)? Может почитаю.



